Все тригонометрические формулы

Обратные тригонометрические функции и простейшие тригонометрические уравнения

Арккосинус

Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.

Если, $|а|≤1$, то $arccos а = t ⇔ \{\table \cos (t)=a; \0≤t≤π;$

$arcos(-a) = π-arccos⁡a$, где $0≤а≤1$

Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение

$t=±arccos ⁡ a+2πk; k∈Z$

Частные случаи

$cos t =1, t = 2πk;k∈Z$

$cos t = 0, t = {π}/{2}+πk;k∈Z$

$cos t = -1, t=π+2πk;k∈Z$

Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$

$сos{2πx}/{3}=-{√3}/{2}$

${2πx}/{3}=±arccos⁡(-{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$

${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$

Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$

$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$

$x=±1,25+3k$

Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения

$k=0$

$x_1= -1,25$

$x_2=1,25$

$к=1$

$х_1=3-1,25=1,75$

$х_2=3+1,25=4,25$

Нам подходит $1,25$ – это и есть результат

Ответ: $1,25$

Арксинус

Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.

Если, $|а|≤1$, то $arcsin a = t ⇔ \{\table \sint=a; \-{π}/{2}≤t≤{π}/{2};$

$arcsin(-a)= — arcsin a$, где $0≤а≤1$

Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:

$1. t_1 = arcsin a+2πk;k∈Z$

$t_2 = (π- arcsin a)+ 2πk;k∈Z$

$2. t=(-1)^n arcsin ⁡ a+πn; n∈Z$

$3.$ Частные случаи

$sin t = 0, t=πk;k∈Z$

$sin t = 1, t={π}/{2}+2πk;k∈Z$

$sin t = -1,t=-{π}/{2}+2πk;k∈Z$

Арктангенс

$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.

$arctg a = t ⇔ \{\table \tgt=a; \-{π}/{2}≤t≤{π}/{2};$

$arctg(-a)= — arctg a$

Тригонометрические формулы сложения углов

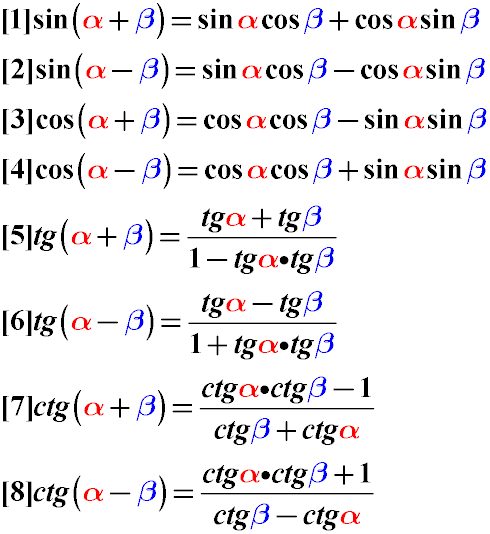
cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Пример задачи на использование формул тригонометрии

sin5x·cos3x − sin8x·cos6x = 0.

Имеем две разные функции sin() и cos() и четыре! разных аргумента 5x, 3x, 8x и 6x. Без предварительных преобразований свести к простейшим типам тригонометрических уравнений не получится. Поэтому сначала пробуем заменить произведения на суммы или разности функций. Делаем это так же, как в примере выше (см. раздел ).

sin(5x + 3x) + sin(5x − 3x) = 2·sin5x·cos3x
sin8x + sin2x = 2·sin5x·cos3x

sin(8x + 6x) + sin(8x − 6x) = 2·sin8x·cos6x
sin14x + sin2x = 2·sin8x·cos6x

(sin8x + sin2x)/2 − (sin14x + sin2x )/2 = 0.

xxxxxx

Уравнение значительно упростилось, но решать его так sin8x = sin14x, следовательно 8x = 14x + T, где Т — период, неверно, так как мы не знаем значения этого периода. Поэтому воспользуемся тем, что в правой части равенства стоит 0, с которым легко сравнивать множители в любом выражении.
Чтобы разложить sin8x − sin14x на множители, нужно перейти от разности к произведению. Для этого можно воспользоваться формулой разности синусов, или снова формулой суммы синусов и нечётностью функции синус (см. пример в разделе ).

sin8x − sin14x = sin8x + sin(−14x) = 2·sin 8x + (−14x)__________   2·cos 8x − (−14x)__________   2  = sin(−3x)·cos11x = −sin3x·cos11x.

Итак, уравнение sin8x − sin14x = 0 равносильно уравнению sin3x·cos11x = 0, которое, в свою очередь, равносильно совокупности двух простейших уравнений sin3x = 0 и cos11x = 0. Решая последние, получаем две серии ответовx₁ = πn/3, nϵZx₂ = π/22 + πk/11, kϵZ

Если Вы обнаружили ошибку или опечатку в тексте, сообщите о ней, пожалуйста, на электронный адрес [email protected]. Буду весьма признательна.

 Перейти  на главную страницу сайта.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы?   пожелания?  замечания? Обращайтесь —
  [email protected]

Внимание, mathematichka. Прямое копирование материалов на других сайтах запрещено

Ставьте ссылки.

Доказательство

Начнем с доказательства формулы косинуса разности . Она нам поможет доказать другие формулы сложения.

Перед доказательством стоит озвучить один не очень очевидный факт, который мы используем. Он заключается в следующем. Возьмем единичную окружность. Пусть точки A₁ и A₂ получены в результате поворота начальной точки A(1, 0) вокруг точки O на углы и соответственно. Тогда угол между векторами и равен либо , либо , где z – любое целое число. Другими словами, угол между указанными векторами равен либо , либо , либо отличается от этих значений на целое число полных оборотов. Приведем графическую иллюстрацию для наглядности.

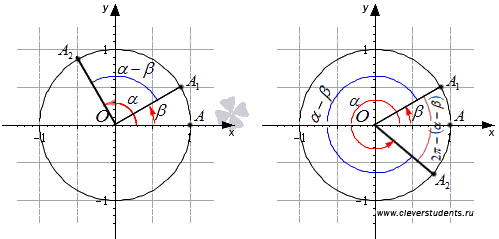
Более того, формулы приведения позволяют нам записать следующие результаты и . Таким образом, косинус угла между векторами и равен косинусу угла , то есть, . Теперь можно переходить непосредственно к доказательству формулы косинуса разности.

В силу определений синуса и косинуса, точки A₁ и A₂ имеют координаты и соответственно. Тогда и (при необходимости смотрите координаты векторов через координаты точек их начала и конца). Длины этих векторов равны единице, так как они равны радиусу единичной окружности.

Теперь запишем скалярное произведение векторов и . С одной стороны имеем , а это же скалярное произведение в координатах имеет вид . Отсюда получаем равенство . Этим доказана формула косинуса разности.

Переходим к доказательству следующей формулы сложения. Формулу косинуса суммы легко доказать, используя уже доказанную формулу и представление вида . Имеемпоследний переход возможен в силу свойств синуса и косинуса противоположных углов.

Из формулы косинуса разности легко получить формулу синуса суммы, достаточно лишь обратиться к формуле приведения вида . Так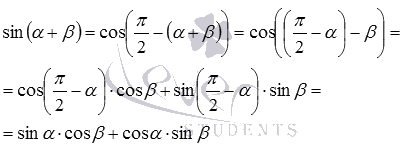в последнем переходе мы использовали формулы приведения.

А вот доказательство формулы синуса разности:в последнем переходе использовалось свойство синуса и косинуса противоположных углов.

Переходим к доказательству формул сложения для тангенса и котангенса. Для этого достаточно вспомнить, что тангенс – это отношение синуса к косинуса, а котангенс – отношение косинуса к синусу, а также применить доказанные выше формулы.

Так 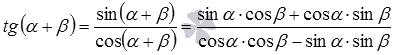. Теперь разделим числитель и знаменатель полученной дроби на , учитывая что и , имеем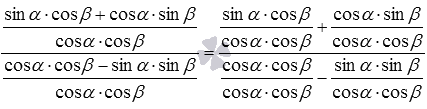после сокращения дробей получаем .В итоге имеем .

Теперь докажем формулу тангенса разности: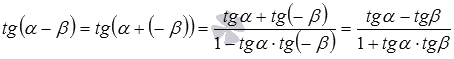

Формулы сложения для котангенса доказываются аналогично формулам сложения для тангенса: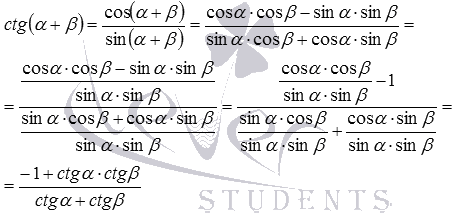и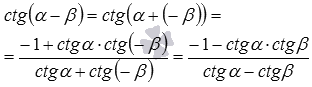

Уроки арифметики на українській мові

• Урок №2. Додавання натуральних чисел
• Урок №3. Віднімання натуральних чисел
• Урок №4. Таблиця множення
• Урок №5. Множення натуральних чисел
• Урок №6. Ділення натуральних чисел
• Урок №8. Величини та їх вимірювання
• Урок №10. Подільність чисел
• Урок №13. Звичайні дроби
• Урок №15. Додавання дробів
• Урок №16. Віднімання дробів
• Урок №17. Множення дробів
• Урок №18. Ділення дробів
• Урок №21. Кінечни десяткові дроби
• Урок №22. Додавання десяткових дробів
• Урок №23. Віднимання десяткових дробів
• Урок №24. Множення десяткових дробів
• Урок №25. Ділення десяткових дробів
• Урок №18. Нескінченний десятковий дріб
• Урок №19. Відношення величин
• Урок №20. Пропорції
• Урок №6. Відсотки
• Урок №7. Відсотки (2)
• Урок №12. Середнє арифметичне
• Урок №14. Масштаб

Решение простейших тригонометрических уравнений

Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.

Чтобы решить такое тригонометрическое уравнение, нужно воспользоваться тригонометрической окружностью, найти значение тригонометрической функции на оси этой функции и записать значения точек с периодом, так как данные функции периодические.

Рассмотрим решение таких уравнений на примерах.

Пример 1:\(cos\:x = -\frac{1}{2}\)

Найдём на тригонометрической окружности точки, для которых значение косинуса равно \(-\frac{1}{2}\)

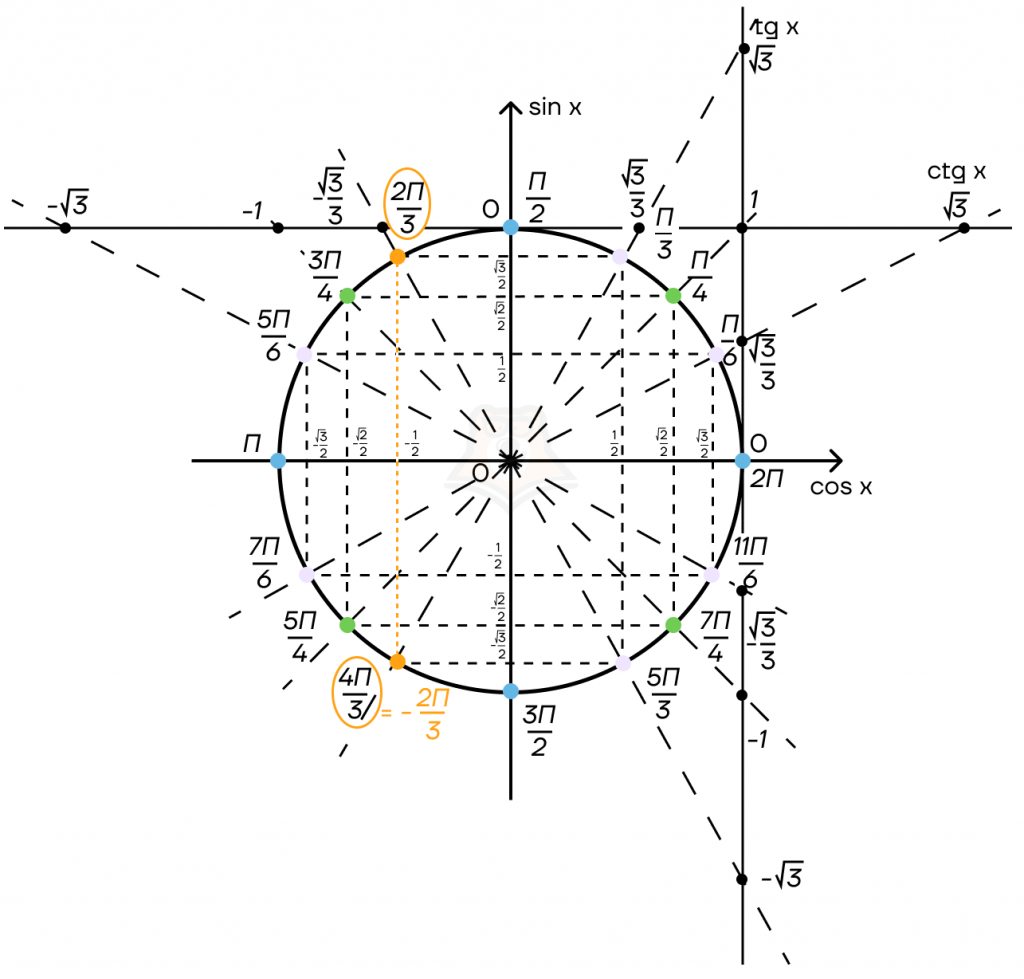
На окружности есть две таких точки. При этом вторую точку можно отложить на отрицательном направлении, тогда решения можно записать следующим образом:

\(x = \pm \frac{2 \pi}{3} + 2 \pi k, k \in Z\)

Важно: обязательно нужно прописывать период, так как точки на данных местах, находящиеся на всех витках спирали, будут иметь такое значение косинуса. Пример 2:\(sin\:x = \frac{1}{2}\)

Пример 2:\(sin\:x = \frac{1}{2}\)

Проведем перпендикулярную к оси синусов линию через значение \(\frac{1}{2}\). Запишем эти две точки в виде совокупности.

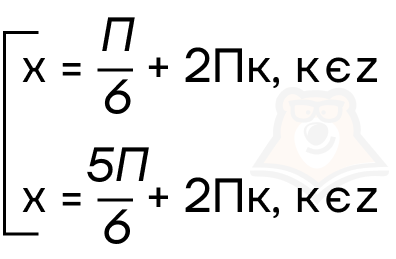
Пример 3:tg x = 1 

Найдем нужное значение на оси тангенсов. Проведем линию и заметим, что в ответ должны идти две диаметрально противоположные точки. Следовательно, можно записать начальную точку, но с периодом в половину окружности, то есть  πk, где  k ∈ Z

\(x = \frac{\pi}{4} + \pi k, k \in Z\)

Пример 4:\(ctg\:x = \sqrt{3}\)

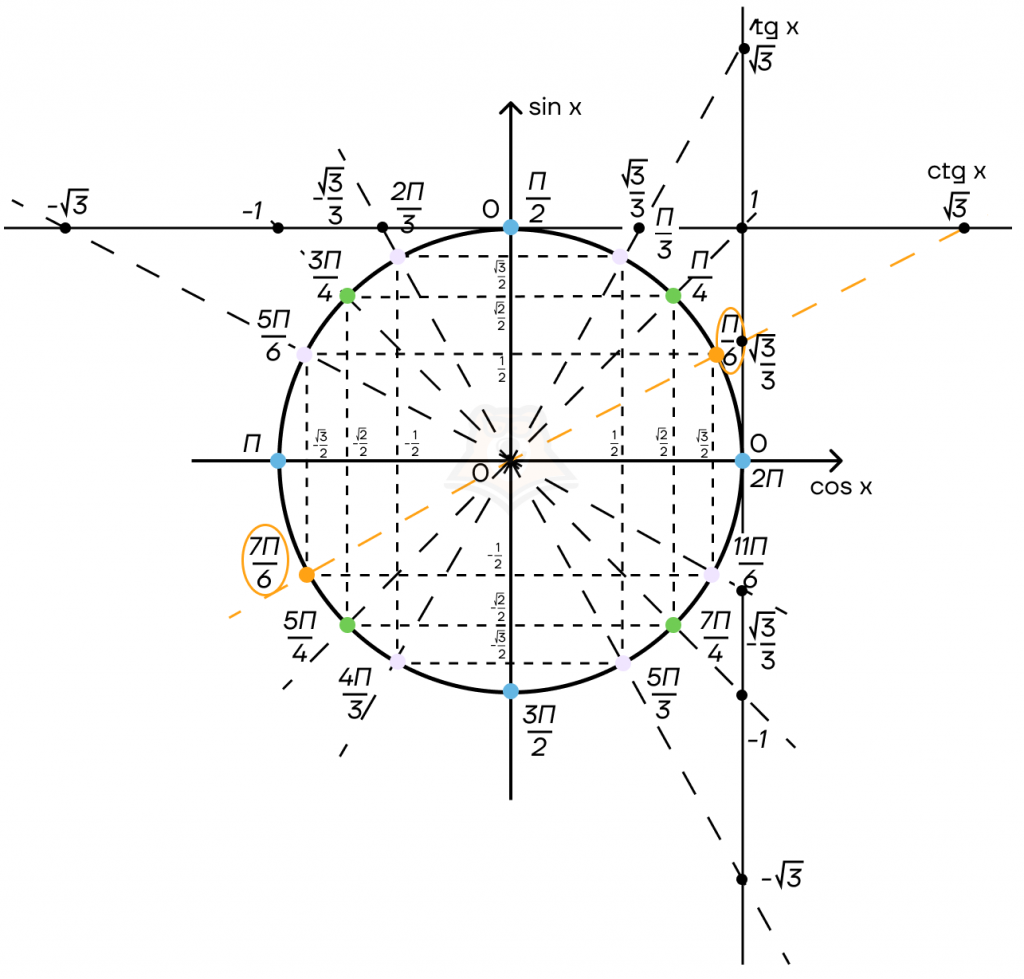
Найдем \(\sqrt{3}\) на оси котангенсов и проведём прямую, найденные точки будут диаметрально противоположными. Поэтому запишем первую точку с периодом в половину окружности.

\(x = \frac{\pi}{6} + \pi k, k \in Z\)

Алгоритм решения простейших тригонометрических уравнений:1) Найти значение тригонометрической функции на оси этой функции на тригонометрической окружности.2) Отметить точки.3) Записать точки.

Уроки арифметики на русском языке

• Урок №2. Сложение натуральных чисел
• Урок №3. Вычитание натуральных чисел
• Урок №4. Таблица умножения
• Урок №5. Умножение натуральных чисел
• Урок №6. Деление натуральных чисел
• Урок №8. Величины и их измерение
• Урок №10. Делимость чисел
• Урок №13. Обыкновенные дроби
• Урок №15. Сложение дробей
• Урок №16. Вычитание дробей
• Урок №17. Умножение дробей
• Урок №18. Деление дробей
• Урок №21. Конечные десятичные дроби
• Урок №22. Сложение десятичных дробей
• Урок №23. Вычитание десятичных дробей
• Урок №24. Умножение десятичных дробей
• Урок №25. Деление десятичных дробей
• Урок №26. Округление чисел
• Урок №1. Отношение величин
• Урок №2. Пропорции
• Урок №6. Проценты
• Урок №7. Нахождение процентов данного числа
• Урок №12. Среднее арифметическое
• Урок №14. Масштаб

Формулы тригонометрии — коротко о главном

Основные формулы:

Название формулы	Формула
Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!)	\( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\)
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)	\( \displaystyle tg\ \alpha =\frac{sin\ \alpha }{cos\ \alpha }\)
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)	\( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }=\frac{1}{tg\ \alpha }\)
Синус суммы и разности:	\( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \)
Косинус суммы и разности:	\( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \)
Тангенс суммы и разности:	\( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\)

Формулы понижения степени:

Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.

• \( \displaystyle si{{n}^{2}}\alpha =\frac{1-cos2\alpha }{2}\)
• \( \displaystyle co{{s}^{2}}\alpha =\frac{1+cos2\alpha }{2}\)
• \( \displaystyle si{{n}^{3}}\alpha =\frac{3sin\alpha -sin3\alpha }{4}\)
• \( \displaystyle co{{s}^{3}}a=\frac{3cosa+cos3a}{4}\)
• \( \displaystyle t{{g}^{2}}\alpha =\frac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \frac{\pi }{2}+\pi n,n\in Z\)

Формулы преобразования функций:

Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.

• \( \displaystyle sin\alpha \pm sin\beta =2sin\frac{\alpha \pm \beta }{2}cos\frac{\alpha \mp \beta }{2}\)
• \( \displaystyle cos\alpha +cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}\)
• \( \displaystyle cos\alpha -cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}\)
• \( \displaystyle tg\alpha \pm tg\beta =\frac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta }\)
• \( \displaystyle ctg\alpha \pm ctg\beta =\frac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta }\)

Формулы преобразования произведений функций:

• \( \displaystyle sin\alpha sin\beta =\frac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2}\)
• \( \displaystyle sin\alpha cos\beta =\frac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2}\)
• \( \displaystyle cos\alpha cos\beta =\frac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2}\)

Таблица значений тригонометрических функций:

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

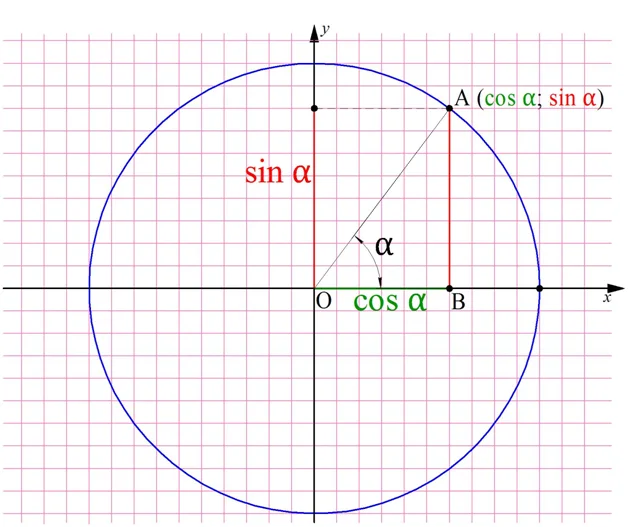
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ2 + ОВ2 = ОА2

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin2α + соs2α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin2α + соs2α = 1

0,82 + соs2α = 1

0,64 + соs2α = 1

соs2α = 1 – 0,64

соs2α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

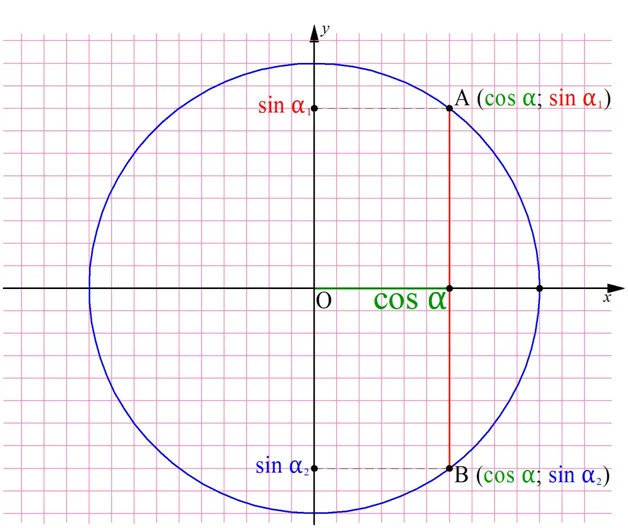
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin2α + соs2α = 1

0,282 + sin2α = 1

0,0784 + sin2α = 1

sin2α = 1 – 0,0784

sin2α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin2α + соs2α = 1

соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin2α + соs2α = 1

Далее поделим его на величину соs2α:

Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:

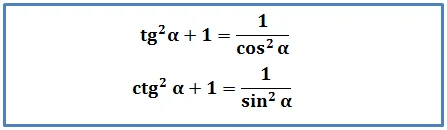
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin2α + соs2α = 1

sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения

sin2α = 1 – соs2α

и

соs2α = 1 – sin2α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin2α + 9соs2α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin2α = 1 – соs2α:

4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =

= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs2α – 2.

Задание. Избавьтесь от синуса в выражении

sin4α – соs4α

Решение. Воспользуемся ф-лой :

sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =

= 1 – соs2α– соs2α = 1 – 2 соs2α

Ответ:1 – 2 соs2α.

Задание. Упростите дробь

Решение.

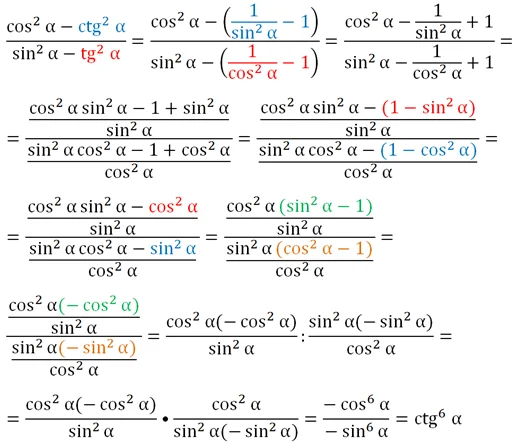
Ответ: ctg6α.

Как запомнить формулы приведения

Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.

Поэтому познакомимся с мнемоническим алгоритмом:

1. Представьте аргумент в виде , где n — целое число, а — острый угол, то есть принадлежит отрезку

2. Изобразите (на листе или мысленно) на единичной окружности данный угол.

3. С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

   Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:

4. Если в аргументе у опорной точки n — нечетное число, то исходную функцию замените на кофункцию, то есть на противоположную функцию (синус меняется на косинус, тангенс — на котангенс, и наоборот).

   Если в аргументе у опорной точки n — четное число, то функция не меняется.

Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».

Правило лошадки
Когда вы во втором шаге изобразили на единичной окружности угол, обратите внимание на положение опорной точки. Если она располагается на вертикальной оси, то при вопросе «Меняется ли функция?» лошадка кивает головой вверх-вниз и отвечает: «Да»

Если опорная точка располагается на горизонтальной оси, то лошадка мотает головой влево-вправо и отвечает: «Нет, функция не меняется».

Таким образом, формулы приведения — это тригонометрические тождества вида

Задание 1

Найдите значение выражения

Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.

1. Сначала нужно представить аргумент в виде , где n — целое число, а — острый угол. Здесь этот шаг уже выполнен, поэтому пропускаем его.

2. Далее изображаем данный угол на тригонометрической окружности:

3. Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.

4. В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка лежит на горизонтальной оси, значит, функция не меняется на кофункцию, то есть синус не меняется на косинус.

Значит, .

Приведем аналогичные рассуждения для всех слагаемых в выражении.

1. Аргумент уже представлен в виде , где n — целое число, а — острый угол.

2. Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.

3. Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит, .

1. Аргумент уже представлен в виде , где n — целое число, а — острый угол.

2. Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.

3. Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит, .

А теперь запишем преобразованные выражения в наше исходное и упростим:

Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение

Задание 2

До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.

Разберем на примере: найдите значение выражения .

В этом случае важно заметить, что , а значит, одну из функций, например , можно представить в виде , то есть в виде, необходимом для использования формулы приведения. Так как первый шаг выполнен, то продолжаем идти по алгоритму

Так как первый шаг выполнен, то продолжаем идти по алгоритму.

Косинус в первой четверти тригонометрической окружности принимает положительные значения.

Опорная точка лежит на вертикальной оси, поэтому косинус меняется на синус.

Значит,

Запишем преобразованные выражения в наше исходное и упростим:

Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart

Выражение одних тригонометрических функций через другие

`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`

Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.

Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.

Материалы по теме:

• Тригонометрические формулы: косинус, синус и тангенс двойного угла
• Формулы половинного угла тригонометрических функций
• Формулы понижения степени в тригонометрии: вывод и примеры
• Таблица неопределённых интегралов

Произведение тригонометрических функций

В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:

Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):

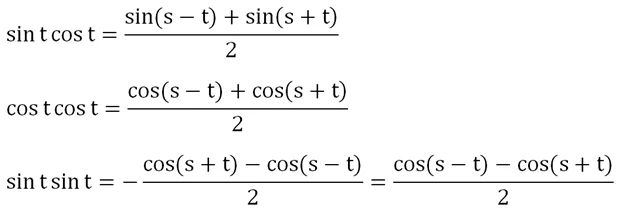
В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.

Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.

Задание. Преобразуйте произведение в сумму:

Решение.

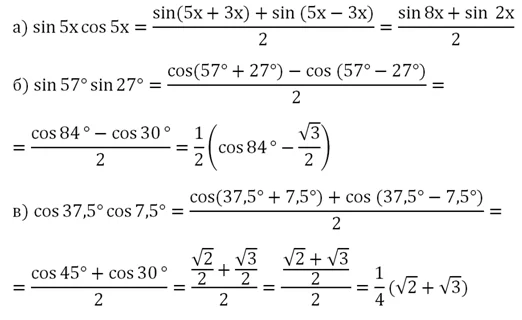
На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.

В самом конце приведем перечень всех формул, выведенными в этом уроке:

I группа. Основные тождества

sin2α + cos2α = 1;

tgα = ____sinαcosα ;     ctgα = ____cosαsinα ;

tgα·ctgα = 1;

1 + tg2α = _____   1cos2α;     1 + ctg2α = _____   1sin2α .

Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).

Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___  1tgα и пользуйтесь формулами для тангенса.

Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю

Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.