Таблица производных. доказательство формул

Таблица производных часто встречающихся функций

В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.

Функция	Формула для производной	Название формулы
y = c , где c – любое число	y’ = 0	Производная от постоянной функции
y = x c , где c – любое число	y’ = c xc – 1	Производная степенной функции
y = e x	y’ = e x	Производная от экспоненты (показательной функции с основанием e)
y = a x где a – любое положительное число, не равное 1	y’ = a x ln a	Производная от показательной функции с основанием a
y = ln x , x > 0	, x > 0	Производная от натурального логарифма
y = log a x , x > 0 где a – любое положительное число, не равное 1	, x > 0	Производная от логарифма по основанию a
y = sin x	y’ = cos x	Производная синуса
y = cos x	y’ = – sin x	Производная косинуса
y = tg x ,	, ,	Производная тангенса
y = ctg x ,	, ,	Производная котангенса
y = arcsin x ,		Производная арксинуса
y = arccos x ,		Производная арккосинуса
y = arctg x		Производная арктангенса
y = arcctg x		Производная арккотангенса

Производная от постоянной функции

Функция: y = c , где c – любое число Формула для производной: y’ = 0

Производная степенной функции

Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1

Производная от экспоненты (показательной функции с основанием e)

Функция: y = e x Формула для производной: y’ = e x

Производная от показательной функции с основанием a

Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a

Производная от натурального логарифма

Функция: y = ln x , x > 0 Формула для производной: , x > 0

Производная от логарифма по основанию a

Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: , x > 0

Производная синуса

Функция: y = sin x Формула для производной: y’ = cos x

Производная косинуса

Функция: y = cos x Формула для производной: y’ = – sin x

Производная тангенса

Функция: y = tg x , где Формула для производной: ,

Производная котангенса

Функция: y = ctg x , где Формула для производной: ,

Производная арксинуса

Функция: y = arcsin x , Формула для производной:

Производная арккосинуса

Функция: y = arccos x , Формула для производной:

Производная арктангенса

Функция: y = arctg x Формула для производной:

Производная арккотангенса

Функция: y = arcctg x Формула для производной:

Производная и тригонометрические функции

Тригонометрические функции неразрывно связаны с производной. Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция Y = f (x) – синяя кривая.

K (x0; f (x0)) – произвольная точка, x0 + ∆x – приращение по оси OX, а f (x0 + ∆x) – приращение по оси OY в некой точке L.

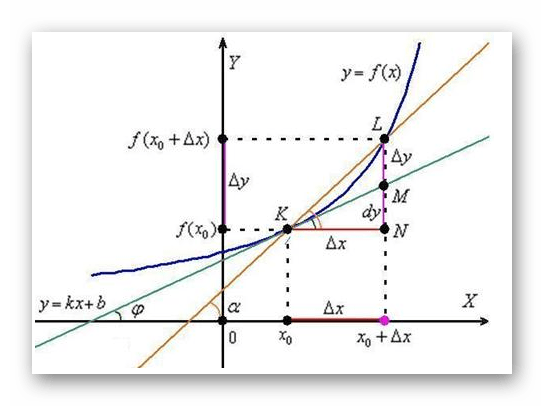
Проведем прямую через точки K и L и построим прямоугольный треугольник KLN. Если мысленно перемещать отрезок LN по графику Y = f (x), то точки L и N будут стремиться к значениям K (x0; f (x0)). Назовем эту точку условным началом графика — лимитом, если же функция бесконечна, хотя бы на одном из промежутков – это стремление также будет бесконечным, а его предельное значение близким к 0.

Характер данного стремления можно описать касательной к выбранной точке y = kx + b или графиком производной первоначальной функции dy – зеленая прямая.

Но где же здесь тригонометрия?! Все очень просто рассмотрим прямоугольный треугольник KLN. Значение дифференциала для конкретной точки K есть тангенс угла α или ∠K:

Таким образом можно описать геометрический смымсл производной и ее взаимосвязь с тригонометрическими функциями.

Решение задачи B15 с тригонометрией

С теорией разобрались, давайте решать нашу задачу. Для начала нам нужно посчитать производную функции:

Производная тригонометрической функции

Итак, записываем:

И вот тут возникает проблема в данной задаче: дело в том, что внутри синуса и косинуса стоит не переменная х, а выражение 2х и даже 4х.

Как поступать с такими конструкциями? Конечно, можно воспользоваться производной сложной функции, посчитать и в итоге получить правильное значение, но давайте не будем лезть в дебри, а вспомним замечательную формулу, которая рассматривалась не нескольких уроках, посвященным подготовке к ЕГЭ по математике. Формула следующая:

Другими словами, замена переменной функции не проходит для всей функции бесследно. В случае, если вместо х мы подставляем линейную функцию, то перед новой производной появляется коэффициент.

Это частный случай производной сложной функции. Однако сложные функции в реальном ЕГЭ не встречаются. Поэтому вам достаточно будет знать упрощенную конструкцию, которую мы записали. Ее очень легко применять.

Производная функции при линейной замене

Давайте посчитаем производную sin 2. Для этого вспомним такое:

Тогда производная от sin 2 будет выглядеть так:

Все, производная 2sin 2 найдена. Аналогично давайте разберемся и с производной cos 4:

А теперь собираем это все в одну конструкцию и получаем:

Считаем нули производной — точки экстремума

Итак, первый шаг нашего алгоритма выполнен, мы нашли производную. Теперь приравниваем эту производную к нулю и решаем полученное уравнение:

Перед нами обычное тригонометрическое уравнение и все, что нам требуется сделать в нем — это свести все тригонометрические функции к одному и тому же аргументу. Как правило, в таких задачах следует стремиться к наименьшему аргументу. Поэтому вспомним формулу двойного угла:

В нашем случае это будет выглядеть так:

Обратите внимание! Мы пишем именно 2х, потому что в исходной формуле, которую мы разложили, вместо переменной λ стоит именно 2х. Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта

Получим:

Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта. Получим:

Итак, мы разложили наше уравнение на множители. Теперь вспоминаем: произведение равно нулю, когда хотя бы один из множителей равен нулю. Запишем:

Первое уравнение решается элементарно:

А со вторым уравнением будет немного посложнее:

Напомню, что решение простейших тригонометрических уравнений, которые содержат синус, лучше записывать как совокупность из двух наборов корней.

Однако на этом решение уравнения еще не закончилось. Взгляните, мы нашли только 2х, а нужно найти просто х. Находим:

Производная тригонометрической функции: отбор корней на отрезке

Уравнение решено. Переходим к третьему шагу: необходимо отобрать корны, которые лежат на отрезке [0; π/3].

Для этого нам сначала потребуется начертить радар, а потом отметить на мне все три набора корней. На этом же отрезке отмечаем концы отрезка. Получим:

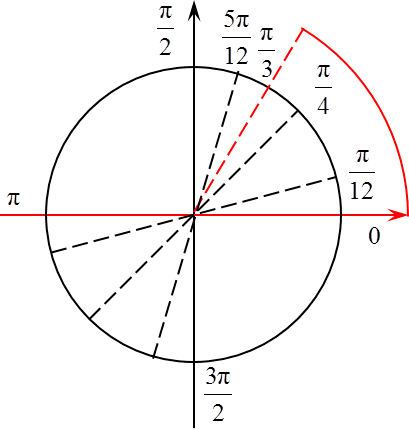
На самом деле из всего этого многообразия нас интересуют лишь две точки: π/4 и π/12. Все, третий шаг выполнен. Мы отобрали корни на отрезке.

Вычисление наибольшего значения функции

А теперь возвращаемся к условию задачи и вспоминаем, что нам нужно найти наибольшее значение функции на отрезке. Т. е. нужно взять функцию

И подставить в нее следующие числа:

1. Оба конца нашего отрезка — числа 0 и π/3
2. А также два корня производной, которую мы нашли: π/4 и π/12

Затем из полученных четырех значений функции надо выбрать наибольшее.

Давайте решать. В первую очередь предлагаю подставить корни нашей производной, т. е. числа π/4 и π/12. Получим:

Итак, (π/4) = 1

Подставляем второе число — = π/12:

Все, с корнями из производной мы разобрались, теперь считаем значение функции на концах отрезка:

Вычисление сложных значений тригонометрической функции

Теперь подставляем правый конец отрезка:

Оба аргумента и в синусе, и в косинусе являются нестандартными значениями (их нет в классической таблице значений тригонометрических функций), поэтому давайте отметим их на тригонометрическом круге:

С помощью полученных данных вычисляем значение функции:

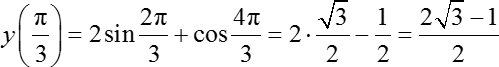
Это иррациональное число, которое нельзя записать в ответ. Следовательно, оно не является ответом к задаче.

Итого нам на выбор осталось три числа: = 1; = 1,5; = 1. Требуется найти наибольшее значение. Следовательно, ответом будет являться = 1,5. Все, задача решена.

Производная обратной функции.

Чтобы
при изложении не было путаницы, давайте
обозначать в нижнем индексе аргумент
функции, по которому выполняется
дифференцирование, то есть, —
это производная функции f(x)
по x
.

Теперь
сформулируем правило
нахождения производной обратной функции.

Пусть
функции y
= f(x)
и x
= g(y)
взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x)
,
то в точке существует
конечная производная обратной
функции g(y)
,
причем .
В другой записи .

Можно
это правило переформулировать для
любого x
из
промежутка ,
тогда получим .

Давайте
проверим справедливость этих формул.

Найдем
обратную функцию для натурального
логарифма (здесь y
–
функция, а x
—
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть, и взаимно
обратные функции.

Из таблицы
производных видим,
что и .

Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:

Как
видите, получили такие же результаты
как и в таблице производных.

Теперь
мы обладаем знаниями для доказательства
формул производных обратных
тригонометрических функций.

Начнем
с производной арксинуса.

.
Тогда по формуле производной обратной
функции получаем

Осталось
провести преобразования.

Так
как областью значений арксинуса является
интервал ,
то (смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.

Следовательно, .
Областью определения производной
арксинуса является промежуток (-1;
1)
.

Для
арккосинуса все делается абсолютно
аналогично:

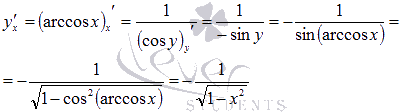
Найдем
производную арктангенса.

Для обратной
функцией является .

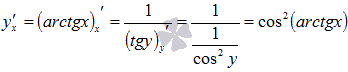
Выразим
арктангенс через арккосинус, чтобы
упростить полученное выражение.

Пусть arctgx
= z
,
тогда

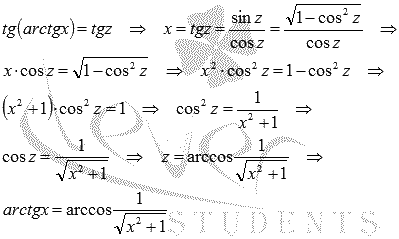
Следовательно,

Схожим
образом находится производная
арккотангенса:

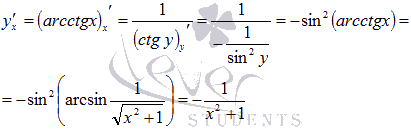
Производная

Вычисление производной от математической функции (дифференцирование) является очень частой задачей при решении высшей математики. Для простых (элементарных) математических функций это является довольно простым делом, поскольку уже давно составлены и легко доступны таблицы производных для элементарных функций. Однако, нахождение производной сложной математической функции не является тривиальной задачей и часто требует значительных усилий и временных затрат.

Найти производную онлайн

Использование нашего сервера позволит вам 1) вычислить производную онлайн за вас, избавив от длительных и утомительных вычислений, в ходе которых вы могли бы допустить ошибку или опечатку; 2) если вы вычисляете производную математической функции самостоятельно, то мы предоставляем вам возможность сравнить полученный результат с вычислениями нашего сервиса и убедиться в верности решения либо отыскать закравшуюся ошибку; 3)пользоваться нашим сервисом вместо использования таблиц производных простых функций, где зачастую необходимо время для нахождения нужной функции.

Всё что от вас требуется, чтобы найти производную онлайн
— это воспользоваться нашим сервисом на

Приведем сводную таблицу для удобства и наглядности при изучении темы.

Константа y = C Степенная функция y = x p (x p) » = p · x p — 1	Показательная функция y = a x (a x) » = a x · ln a В частности, при a = e имеем y = e x (e x) » = e x
Логарифмическая функция (log a x) » = 1 x · ln a В частности, при a = e имеем y = ln x (ln x) » = 1 x	Тригонометрические функции (sin x) » = cos x (cos x) » = — sin x (t g x) » = 1 cos 2 x (c t g x) » = — 1 sin 2 x
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (a r c t g x) » = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2	Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x) » = 1 c h 2 x (c t h x) » = — 1 s h 2 x

Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный. 

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция. 

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin2α + cos2α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая. 

sin2α + cos2α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности. 

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

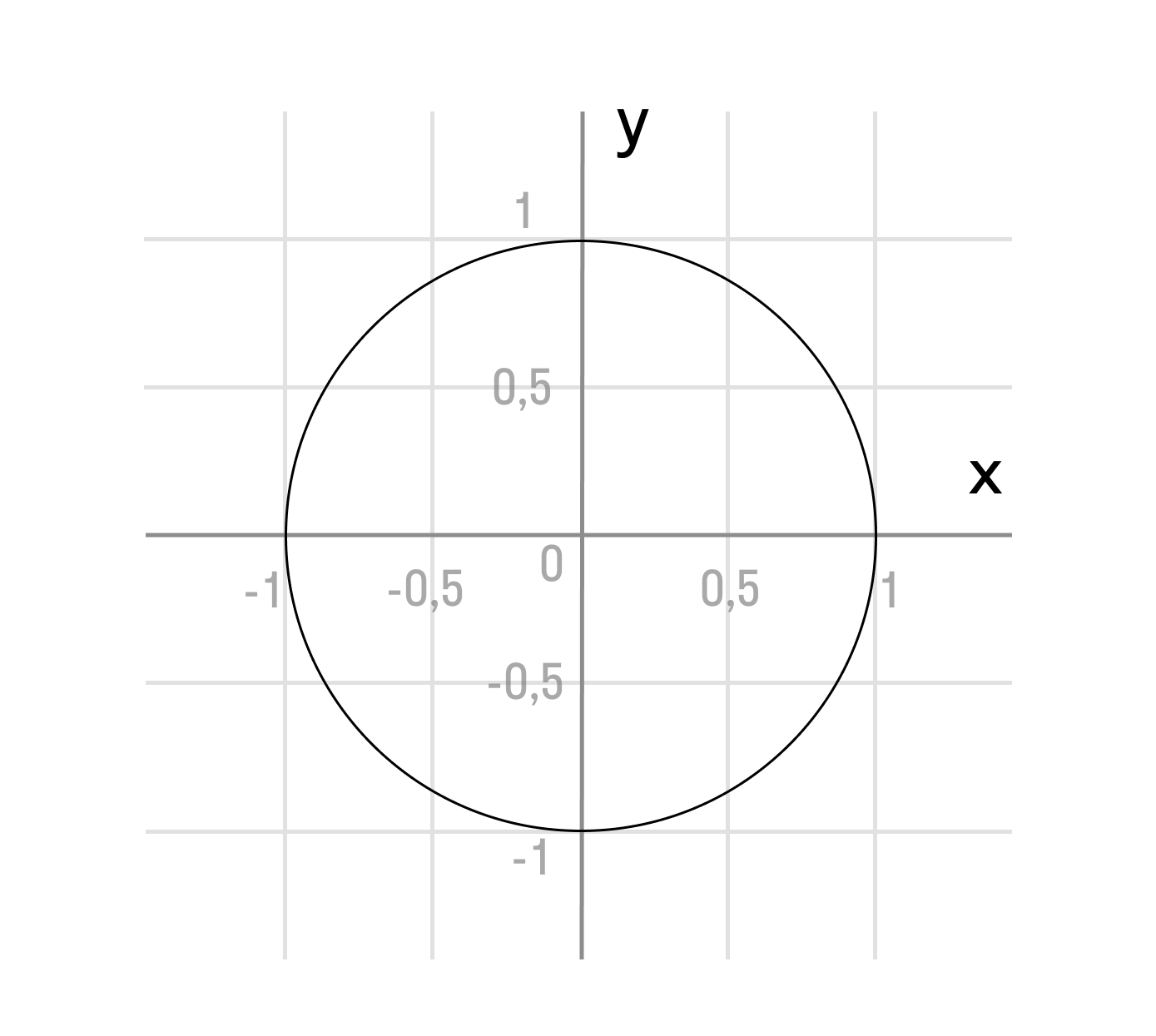
Докажем тождество sin2α + cos2α = 1

1. Итак, нам известны координаты точки A (1; 0). Произвольный угол α, тогда cos α = x0 = ОB.
2. Если развернуть точку A на угол α, то точка A становится на место точки A₁.
3. По определениям:
   • Синус угла (sin α) — это отношение противолежащего катета к гипотенузе. 
   • Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

   Это значит, что точка A₁ получает координаты cos α, sin α.

4. Опускаем перпендикулярную прямую A₁B на x0 из точки A₁. Образовался прямоугольный треугольник OA₁B. |A₁B| = |у| |OB| = |x|.
5. Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности. |OA₁| = 1.
6. Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой: |A₁B|2 + |OB|2 = |OA₁|2.
7. Записываем в виде: |y|2 + |x|2 = 12. Это значит, что y2 + x2 = 1. sin угла α = y cos угла α = x
8. Вставляем данные угла вместо координат точек: OB = cos α A₁B = sin α A₁O = 1
9. Получаем основное тригонометрическое тождество: sin2α + cos2α = 1. Что и требовалось доказать. 

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

• sin α = ±
• cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Производная от синуса

Производная от синуса x получается путём стандартной процедуры для вывода производных, а именно, функция $y$, равная $\sin x$ рассматривается как функция $f$ от икс: $f(x)= \sin x$. Рассмотрим функцию $y$ в точке $x$, придав ей приращение, равное $Δx$:

$f(x+ Δx)=\sin(x + Δx)$;

Напишем, чему равно приращение $Δy$ в этом случае:

$Δy=f(x + Δx) — f(x)=\sin(x + Δx)-\sin x\left(1\right)$

Вспомним формулу разности синусов, она выглядит следующим образом:

$\sin α — \sin β = 2 \sin \frac{α-β}{2} \cdot \cos{α + β}$

Применим её для преобразования полученного нами ранее равенства $(1)$:

$\sin(x + Δx)-\sin x=2\sin x \frac{ (x + Δx)-x}{2} \cdot \cos \frac{ (x + Δx)-x}{2} = 2 \sin \frac{Δx}{2} \cdot \cos \frac{2x+Δx}{2}=2 \sin \frac{ Δx}{2} \cos(x+\frac{Δx}{2})$.

Теперь рассмотрим, чему равно отношение приращения $y$ к приращению $x$:

$\frac{Δy}{Δx}=\frac{2 \sin \frac{Δx}{2} \cos(x+\frac{Δx}{2})}{Δx}\left(2\right)$.

Обозначим дробь $\frac{Δx}{2}$ за новую переменную, назовём её $a$ и перепишем выражение $(2)$ с её использованием:

$\frac{Δy}{Δx}=\frac{\sin a \cos (x+a)}{a}\left(2\right)$.

Определим, чему равен предел выражения $(3)$ при $Δx \to 0$:

$\lim_{Δx \to 0} \frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{\sin a \cos (x+a)}{a}\left(3\right)$.

Так как $Δx \to 0$, а $a$ есть не что иное, как $\frac{Δx}{2}$, то $a$ также стремится к нулю. Перепишем выражение $(3)$ в соответствии с этим:

$\lim_{a \to 0} \frac{Δy}{Δx}=\lim_{a \to 0} \frac{\sin a}{a} \cdot \lim_{a \to 0} \cos(x+a)$.

Первый предел в получившемся выражении равен единице, а второй, так как функция косинуса непрерывна, равен $\cos x$.

Таким образом, мы с вами вывели доказательство того, что производная от $\sin x$ равна косинусу

$(\sin x)’= \cos x$.

Пример 1

Найти, чему равны производные функций:

1. y=sin x+ 3

2. y=4sin x+ cos x.

Решение:

1. $ (\sin x+ 3)’=\cos x$

2. $(4sin x+ cosx)’=4\cos x — \sin x$

Производные тригонометрических функций.

Для
вывода формул производных тригонометрических
функций нам придется вспомнить некоторые
формулы тригонометрии, а также первый
замечательный предел.

По
определению производной для функции
синуса имеем .

Воспользуемся
формулой разности синусов:

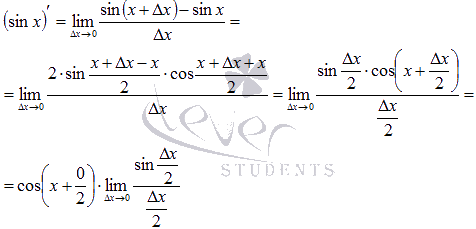
Осталось
обратиться к первому замечательному
пределу:

Таким
образом, производная функции sin
x
есть cos
x
.

Абсолютно
аналогично доказывается формула
производной косинуса.

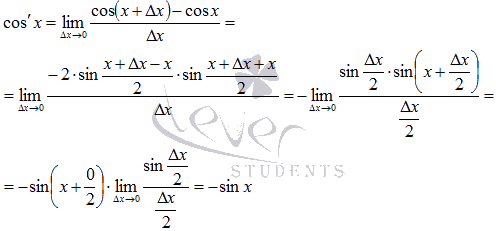
Следовательно,
производная функции cos
x
есть –sin
x
.

Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).

Производная степенной функции

Переходим к степенной функции и формуле ее производной, имеющей вид: (x p) » = p · x p — 1 , где показатель степени p
является любым действительным числом.

Доказательство 2

Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …

Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:

(x p) » = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x

Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:

(x + ∆ x) p — x p = C p 0 + x p + C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p — x p = = C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p

Таким образом:

(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 + C p 2 · x p — 2 · ∆ x + . . . + C p p — 1 · x · (∆ x) p — 2 + C p p · (∆ x) p — 1) = = C p 1 · x p — 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p — 1) ! · x p — 1 = p · x p — 1

Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.

Доказательство 3

Чтобы привести доказательство для случая, когда p —
любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.

Рассмотрим два случая: когда x
положительны и когда x
отрицательны.

Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:

y = x p ln y = ln x p ln y = p · ln x

На данном этапе получили неявно заданную функцию. Определим ее производную:

(ln y) » = (p · ln x) 1 y · y » = p · 1 x ⇒ y » = p · y x = p · x p x = p · x p — 1

Теперь рассматриваем случай, когда x –
отрицательное число.

Если показатель p
есть четное число, то степенная функция определяется и при x

Тогда x p

Если p
есть нечетное число, тогда степенная функция определена и при x

y » (x) = (- (- x) p) » = — ((- x) p) » = — p · (- x) p — 1 · (- x) » = = p · (- x) p — 1 = p · x p — 1

Последний переход возможен в силу того, что если p
— нечетное число, то p — 1
либо четное число, либо нуль (при p = 1), поэтому, при отрицательных x
верно равенство (- x) p — 1 = x p — 1 .

Итак, мы доказали формулу производной степенной функции при любом действительном p .

Пример 2

Даны функции:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12

Определите их производные.

Решение

Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:

f 1 (x) = 1 x 2 3 = x — 2 3 ⇒ f 1 » (x) = — 2 3 · x — 2 3 — 1 = — 2 3 · x — 5 3 f 2 » (x) = x 2 — 1 4 = 2 — 1 4 · x 2 — 1 4 — 1 = 2 — 1 4 · x 2 — 5 4 f 3 (x) = 1 x log 7 12 = x — log 7 12 ⇒ f 3 » (x) = — log 7 12 · x — log 7 12 — 1 = — log 7 12 · x — log 7 12 — log 7 7 = — log 7 12 · x — log 7 84

Производные высших порядков

Заметим, что производную от cos x
первого порядка можно выразить через косинус следующим образом:.

Найдем производную второго порядка, используя формулу производной сложной функции :.
Здесь .

Заметим, что дифференцирование cos x
приводит к увеличению его аргумента на .
Тогда производная n-го порядка имеет вид:(5)
.

Более строго эту формулу можно доказать с помощью метода математической индукции. Доказательство для n-й производной синуса изложено на странице “Производная синуса ”. Для n-й производной косинуса доказательство точно такое. Нужно только во всех формулах заменить sin на cos.

Тема:
«Производная
тригонометрических функций».Тип урока
– урок закрепления знаний.Форма урока
– интегрированный урок.Место урока в системе уроков по данному
разделу
– обобщающий урок.Цели поставлены комплексно:

• обучающие:
  знать правила
  дифференцирования, уметь применять правила
  вычисления производных при решении уравнений и
  неравенств; совершенствовать предметные, в том
  числе вычислительные, умения и навыки; навыки
  работы с компьютером;
• развивающие:
  развитие
  интеллектуально-логических умений и
  познавательных интересов;
• воспитательные:
  воспитывать адаптивность
  к современным условиям обучения.

Методы:

• репродуктивные и продуктивные;
• практические и словесные;
• самостоятельные работы;
• программированное обучение, Т.С.О.;
• сочетание фронтальной, групповой и
  индивидуальной работы;
• дифференцированного обучения;
• индуктивно-дедуктивный.

Формы контроля:

• устный опрос,
• программированный контроль,
• самостоятельная работа,
• индивидуальные задания на компьютере,
• взаимопроверка с применением диагностической
  карты учащегося.

ХОД УРОКА

I. Организационный момент

II. Актуализация опорных знаний

а) Сообщение целей и задач:

• знать правила дифференцирования, уметь
  применять правила вычисления производных при
  решении задач, уравнений и неравенств;
• совершенствовать предметные, в том числе
  вычислительные, умения и навыки; навыки работы с
  компьютером;
• развивать интеллектуально-логические умения и
  познавательные интересы;
• воспитывать адаптивность к современным
  условиям обучения.

б) Повторение учебного материала

Правила вычисления производных
(повторение формул по компьютеру со звуковым
сопровождением). док.7.

1. Чему равна производная синуса?
2. Чему равна производная косинуса?
3. Чему равна производная тангенса?
4. Чему равна производная котангенса?

III. Устная работа

Найти производную.
Вариант 1.	Вариант 2.
у = 2х + 5.	у = 2х – 5.
у = 4cos х .	у = 3sin х .
у = tg х + ctg х .	у = tg х – ctg х .
у = sin 3х .	у = cos 4х .
Варианты ответов.
	– 4sin х		– 3cos х
1/cos 2 х + 1/sin 2 х	1/cos 2 х –1/sin 2 х	1/sin 2 х –1/cos 2 х
	– 4sin4х		– 3cos3х

Обменяйтесь тетрадями. Отметьте в
диагностических картах верно выполненные
задания знаком +, а неверно выполненные задания
знаком –.

IV. Решение уравнений с помощью
производной

– Как найти точки, в которых производная
равна нулю?

Чтобы найти точки, в которых производная
данной функции равна нулю, нужно:

– определить характер функции,
– найти область определения функции,
– найти производную данной функции,
– решить уравнение f
«(x
) = 0,
– выбрать верный ответ.

Задача 1.

Дано:
у

= х
– sin x
.Найти:
точки, в которых
производная равна нулю.Решение.
Функция определена и
дифференцируема на множестве всех
действительных чисел, так как на множестве всех
действительных чисел определены и
дифференцируемы функции g
(x
) = x

и t
(x
) = – sin x
.
Используя правила дифференцирования, получим f

«(x
) = (x
– sin x
)» = (x
)» – ( sin x
)» = 1 – cos x
.
Если f
«(x
) = 0, то 1 – cos x
= 0.
cos x
= 1/; избавимся
от иррациональности в знаменателе, получим cos x

= /2.
По формуле t
= ± arccos a
+ 2n, n Z, получим: х
=
± arccos /2 + 2n, n Z.Ответ:
х = ± /4 + 2n,
n Z.

V. Решение уравнений по алгоритму

Найти, в каких точках обращается в нуль
производная.

f (x ) = sin x + cos x

f (x ) = sin 2x – x

f (x ) = 2x + cos(4x – )

Ученик может выбрать любой из трёх примеров.
Первый пример оценивается оценкой «3
»,
второй – «4
», третий – «5
».
Решение в тетрадях с последующей
взаимопроверкой. Один ученик решает у доски. Если
решение оказывается неверным, то нужно ученику
вернуться к алгоритму и попытаться решить снова.

Программированный контроль.