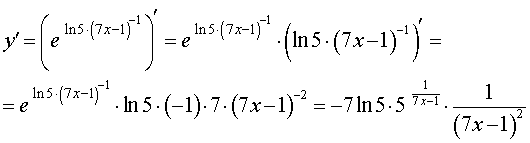Правила вычисления производных. таблица производных часто встречающихся функций. таблица производных сложных функций

Формулы дифференцирования в высшей математике

С помощью таблицы производных решают разнообразные прикладные задания в алгебре. Производная обозначает скорость изменения какой-либо величины. К примеру, если рассмотреть производную у(х) по х, можно определить, с какой скоростью изменяются координаты у по мере изменения координаты х. Если взять производную от скорости, с которой меняется координата у относительно координаты х, то достаточно просто рассчитать ускорение.

Применение производной в задачах по физике позволяет определить производную пути S по времени, то есть скорость. Это связано с тем, что скорость является величиной, характеризующей быстроту изменения расстояния относительно времени. Производная скорости представляет собой ускорение, которое характеризует быстроту изменения скорости.

Заметим, что наличие множества различных функций усложняет процесс дифференцирования. Гораздо проще функцию, записанную из разных элементарных функций, дифференцировать с помощью готовых выражений для производных данных элементарных функций.

При работе с производными удобно пользоваться специальной таблицей. В ней указаны производные простейших функций. В результате получится вычислить производную от любой функции. При этом полезно овладеть навыками дифференцирования. Задача упрощается, благодаря ряду правил дифференцирования.

Дифференцирование подразумевает определение производных и дифференциалов какого-либо порядка от функции одной переменной, частных производных, дифференциалов, полных дифференциалов от функций многих переменных.

Правила дифференцирования

Для выполнения операции нахождения производной существуют определенные правила, которые позволяют правильно произвести взятие дифференциала некоторой функции.

Правила — порядок действий, позволяющих исключить неверные решения задач. Они получены в результате доказательств теорем и следствий из них. Первые необходимы для доказательства некоторых утверждений, которые могут заметно облегчить вычисления.

Простым примером является нахождение гипотенузы прямоугольного треугольника (длины катетов известны). Следует воспользоваться теоремой Пифагора. Нет необходимости доказывать, что квадрат гипотенузы равен сумме квадратов катетов, поскольку это забирает время. Существуют такие свойства (правила) дифференциации:

1. Вынесение константы за знак дифференциала: (C * f(x))’ = C(f(x))’.
2. Если функция представлена в виде суммы (разности) двух функций, то при ее дифференцировании нужно найти производные каждого элемента: (y(x) + z(x))’ = y'(x) + z'(x) и (y(x) — z(x))’ = y'(x) — z'(x).
3. Дифференциал умножения функций f(x) и g(x) равен сумме произведений каждой функции на производную другой: (y(x) * z(x))’ = (y'(x) * z(x) + y(x) * z'(x).
4. Производная частного функций y(x) и z(x) равна числителю, который представляет собой разность произведений знаменателя на дифференциал числителя, и производной знаменателя, умноженного на числитель. Кроме того, знаменатель — квадрат знаменателя исходной дроби: (y(x) / z(x))’ = / (z(x))^2.

Основные правила нахождения производных

Дифференцирование строится на следующих правилах.

Правило №1: производная от произведения числа на функцию равна

(c * f (x))’ = c * f’ (x),

где с – любое число.

Правило №2: производная от суммы функций равна

(f (x) + g (x))’ = f ‘ (x) + g’ (x).

Правило №3: производная от разности функций равна

(f (x) – g (x))’ = f ‘ (x) – g’ (x).

Правило №4: производная от произведения двух функций равна

(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x).

Правило №5: производная от дроби равна

Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.

Правило дифференцирования сложной функции

Производная сложной функции вычисляется по формуле:

‘ = f ‘ (g (x)) g’ (x).

Пример нахождения

Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.

Решение: так как (x¹⁰)’=10x⁹,

то ((x+2) ¹⁰)’=(u¹⁰)’=10u⁹⋅u’=10(x+2) ⁹⋅1=10(x+2) ⁹.

Ответ: 10(x+2) ⁹.

Логарифмическая производная

Логарифмическая производная — это производная от натурального логарифма функции.

Вычисляется по формуле:

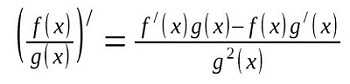
Часто применяется для упрощения дифференцирования некоторых функций.

Пример поиска производной

Пусть y = y(x).

Для удобства прологарифмируем данную функцию:

ln y = ln y(x).

Теперь вычислим производную по правилу дифференцирования сложной функции:

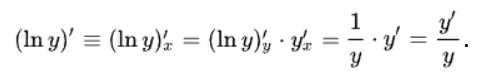
Из этого следует, что

Тогда ответ:

Производная обратной функции

Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.

Общая формула:

Формулы и пример решения

Производные обратных тригонометрических функций:

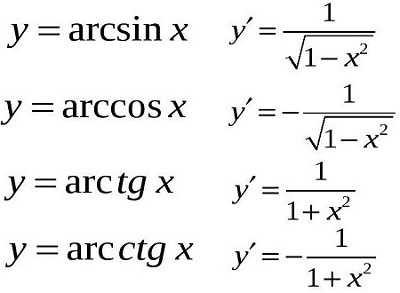
Задача: продифференцировать y=x²-7lnx.

Решение: находим по формуле

отсюда

Производная функции, заданной параметрически

Пусть функция задана параметрическим уравнением:

Тогда производная равна:

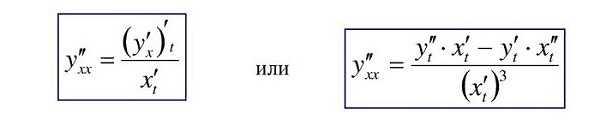
Формулировка, решение примеров

Задача: продифференцировать функцию.

Решение: (при записи производной всегда необходимо писать t в нижнем индексе)

Подставляем в формулу:

Ответ:

В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.

Производная неявной функции

Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.

Теоретическое обоснование

Для нахождения производной неявной функции нужно:

1. Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
2. Решить полученное уравнение относительно производной у’ (х).

Решение в примерах

Задача: решить функцию , заданную неявно:

Решение:

1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства

Получим

Считая, что у – это функция от х, находим производную как от сложной функции:

Тогда

Для заданной функции имеем:

2) Решаем полученное уравнение относительно у’:

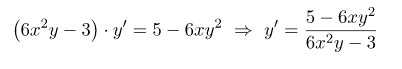
Ответ:

Производные гиперболических функций

Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:

s h » x = e x — e — x 2 » = 1 2 e x » — e — x » = = 1 2 e x — — e — x = e x + e — x 2 = c h x c h » x = e x + e — x 2 » = 1 2 e x » + e — x » = = 1 2 e x + — e — x = e x — e — x 2 = s h x t h » x = s h x c h x » = s h » x · c h x — s h x · c h » x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h » x = c h x s h x » = c h » x · s h x — c h x · s h » x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Производная

Вычисление производной от математической функции (дифференцирование) является очень частой задачей при решении высшей математики. Для простых (элементарных) математических функций это является довольно простым делом, поскольку уже давно составлены и легко доступны таблицы производных для элементарных функций. Однако, нахождение производной сложной математической функции не является тривиальной задачей и часто требует значительных усилий и временных затрат.

Найти производную онлайн

Использование нашего сервера позволит вам 1) вычислить производную онлайн за вас, избавив от длительных и утомительных вычислений, в ходе которых вы могли бы допустить ошибку или опечатку; 2) если вы вычисляете производную математической функции самостоятельно, то мы предоставляем вам возможность сравнить полученный результат с вычислениями нашего сервиса и убедиться в верности решения либо отыскать закравшуюся ошибку; 3)пользоваться нашим сервисом вместо использования таблиц производных простых функций, где зачастую необходимо время для нахождения нужной функции.

Всё что от вас требуется, чтобы найти производную онлайн
— это воспользоваться нашим сервисом на

Решение задачи B15 с тригонометрией

С теорией разобрались, давайте решать нашу задачу. Для начала нам нужно посчитать производную функции:

Производная тригонометрической функции

Итак, записываем:

И вот тут возникает проблема в данной задаче: дело в том, что внутри синуса и косинуса стоит не переменная х, а выражение 2х и даже 4х.

Как поступать с такими конструкциями? Конечно, можно воспользоваться производной сложной функции, посчитать и в итоге получить правильное значение, но давайте не будем лезть в дебри, а вспомним замечательную формулу, которая рассматривалась не нескольких уроках, посвященным подготовке к ЕГЭ по математике. Формула следующая:

Другими словами, замена переменной функции не проходит для всей функции бесследно. В случае, если вместо х мы подставляем линейную функцию, то перед новой производной появляется коэффициент.

Это частный случай производной сложной функции. Однако сложные функции в реальном ЕГЭ не встречаются. Поэтому вам достаточно будет знать упрощенную конструкцию, которую мы записали. Ее очень легко применять.

Производная функции при линейной замене

Давайте посчитаем производную sin 2. Для этого вспомним такое:

Тогда производная от sin 2 будет выглядеть так:

Все, производная 2sin 2 найдена. Аналогично давайте разберемся и с производной cos 4:

А теперь собираем это все в одну конструкцию и получаем:

Считаем нули производной — точки экстремума

Итак, первый шаг нашего алгоритма выполнен, мы нашли производную. Теперь приравниваем эту производную к нулю и решаем полученное уравнение:

Перед нами обычное тригонометрическое уравнение и все, что нам требуется сделать в нем — это свести все тригонометрические функции к одному и тому же аргументу. Как правило, в таких задачах следует стремиться к наименьшему аргументу. Поэтому вспомним формулу двойного угла:

В нашем случае это будет выглядеть так:

Обратите внимание! Мы пишем именно 2х, потому что в исходной формуле, которую мы разложили, вместо переменной λ стоит именно 2х. Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта

Получим:

Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта. Получим:

Итак, мы разложили наше уравнение на множители. Теперь вспоминаем: произведение равно нулю, когда хотя бы один из множителей равен нулю. Запишем:

Первое уравнение решается элементарно:

А со вторым уравнением будет немного посложнее:

Напомню, что решение простейших тригонометрических уравнений, которые содержат синус, лучше записывать как совокупность из двух наборов корней.

Однако на этом решение уравнения еще не закончилось. Взгляните, мы нашли только 2х, а нужно найти просто х. Находим:

Производная тригонометрической функции: отбор корней на отрезке

Уравнение решено. Переходим к третьему шагу: необходимо отобрать корны, которые лежат на отрезке [0; π/3].

Для этого нам сначала потребуется начертить радар, а потом отметить на мне все три набора корней. На этом же отрезке отмечаем концы отрезка. Получим:

На самом деле из всего этого многообразия нас интересуют лишь две точки: π/4 и π/12. Все, третий шаг выполнен. Мы отобрали корни на отрезке.

Вычисление наибольшего значения функции

А теперь возвращаемся к условию задачи и вспоминаем, что нам нужно найти наибольшее значение функции на отрезке. Т. е. нужно взять функцию

И подставить в нее следующие числа:

1. Оба конца нашего отрезка — числа 0 и π/3
2. А также два корня производной, которую мы нашли: π/4 и π/12

Затем из полученных четырех значений функции надо выбрать наибольшее.

Давайте решать. В первую очередь предлагаю подставить корни нашей производной, т. е. числа π/4 и π/12. Получим:

Итак, (π/4) = 1

Подставляем второе число — = π/12:

Все, с корнями из производной мы разобрались, теперь считаем значение функции на концах отрезка:

Вычисление сложных значений тригонометрической функции

Теперь подставляем правый конец отрезка:

Оба аргумента и в синусе, и в косинусе являются нестандартными значениями (их нет в классической таблице значений тригонометрических функций), поэтому давайте отметим их на тригонометрическом круге:

С помощью полученных данных вычисляем значение функции:

Это иррациональное число, которое нельзя записать в ответ. Следовательно, оно не является ответом к задаче.

Итого нам на выбор осталось три числа: = 1; = 1,5; = 1. Требуется найти наибольшее значение. Следовательно, ответом будет являться = 1,5. Все, задача решена.

Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	() = , ∈	0 (да-да, ноль!)
Степень с рациональным показателем	() =	· − 1
Синус	() = sin	cos
Косинус	() = cos	− sin (минус синус)
Тангенс	() = tg	1/cos2
Котангенс	() = ctg	− 1/sin2
Натуральный логарифм	() = ln	1/
Произвольный логарифм	() = log	1/( · ln )
Показательная функция	() =	(ничего не изменилось)

Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:

В общем, константы можно выносить за знак производной. Например:

Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.

«Распаковка» сложной функции

Посмотри на предыдущую функцию еще раз. Сможешь ли ты разобраться в последовательности «упаковки»? Во что икс запихнули сначала, во что потом и так далее до самого конца. То есть — какая функция вложена в какую? Возьми листок и запиши, как ты считаешь. Можно сделать это цепочкой со стрелками как мы писали выше или любым другим способом.

Сделал?

Теперь правильный ответ: сначала икс «упаковали» в \(4\)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию \(2\), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

Например, вот такая функция: \(y=tg⁡(\log_2⁡x )\). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:

\(x → \log_2⁡x → tg⁡(\log_2⁡x )\)

Еще пример: \(y=\cos⁡{(x^3 )}\). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: \(x → x^3 → \cos⁡{(x^3 )}\)

Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть \(\cos⁡{(x·x·x)})\), а там в кубе косинус \(x\) (то есть, \(\cos⁡x·\cos⁡x·\cos⁡x\))

Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): \(y=\sin⁡{(2x+5)}\). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: \(x → 2x+5 → \sin⁡{(2x+5)}\)

И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Как я уже говорил выше, в простых функциях икс «упаковывается» один раз, а в сложных — два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) — тоже простая функция. Например, \(x^7\) – простая функция и \(ctg x\) — тоже. Значит и все их комбинации являются простыми функциями:

\(x^7+ ctg x\) — простая, \(x^7· ctg x\) – простая, \(\frac{x^7}{ctg x}\) – простая и т.д.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:    \(y=cos{⁡(sin⁡x)}\)    \(y=5^{x^7}\)    \(y=arctg⁡{11^x}\)    \(y=log_2⁡(1+x)\) Ответы опять в конце статьи.

Таблица производных сложных функций

В следующей таблице приведены формулы для производных сложных функций.

В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, .

Функция	Формула для производной
y = (kx + b) c , где c – любое число.	y’ = kc (kx + b) c – 1 ,
y = ( f (x)) c , где c – любое число.
y = ekx + b	y = kekx + b
y = e f (x)
y = akx + b где a – любое положительное число, не равное 1
y = a f (x) где a – любое положительное число, не равное 1
y = ln (kx + b) , kx + b > 0	, kx + b > 0
y = ln ( f (x)) , f (x) > 0	, f (x) > 0
y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1	, kx + b > 0
y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1	, f (x) > 0
y = sin (kx + b)	y’ = k cos (kx + b)
y = sin ( f (x))
y = cos (kx + b)	y’ = – k sin (kx + b)
y = cos ( f (x))
y = tg (kx + b), где	, ,
y = tg ( f (x)), где	, ,
y = ctg (kx + b), где	, ,
y = ctg ( f (x)), где	, ,
y = arcsin (kx + b),
y = arcsin ( f (x)),
y = arccos (kx + b),
y = arccos ( f (x)),
y = arctg (kx + b)
y = arctg ( f (x))
y = arcctg (kx + b)
y = arcctg ( f (x))

Функция: y = (kx + b) c , где c – любое число. Формула для производной: y’ = kc (kx + b) c – 1 ,

Функция: y = ( f (x)) c , где c – любое число. Формула для производной:

Функция: y = ekx + b Формула для производной: y = kekx + b

Функция: y = e f (x) Формула для производной:

Функция: y = akx + b где a – любое положительное число, не равное 1 Формула для производной:

Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной:

Функция: y = ln (kx + b) , kx + b > 0 Формула для производной: , kx + b > 0

Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной: , f (x) > 0

Функция: y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 Формула для производной: , kx + b > 0

Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной: , f (x) > 0

Функция: y = sin (kx + b) Формула для производной: y’ = k cos (kx + b)

Функция: y = sin ( f (x)) Формула для производной:

Функция: y = cos (kx + b) Формула для производной: y’ = – k sin (kx + b)

Функция: y = cos ( f (x)) Формула для производной:

Функция: y = tg (kx + b), где Формула для производной: , ,

Функция: y = tg ( f (x)), где Формула для производной: , ,

Функция: y = ctg (kx + b), где Формула для производной: , ,

Функция: y = ctg ( f (x)), где Формула для производной: , ,

Функция: y = arcsin (kx + b), Формула для производной:

Функция: y = arcsin ( f (x)), Формула для производной:

Функция: y = arccos (kx + b), Формула для производной:

Функция: y = arccos ( f (x)), Формула для производной:

Функция: y = arctg (kx + b) Формула для производной:

Функция: y = arctg ( f (x)) Формула для производной:

Функция: y = arcctg (kx + b) Формула для производной:

Функция: y = arcctg ( f (x)) Формула для производной:

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

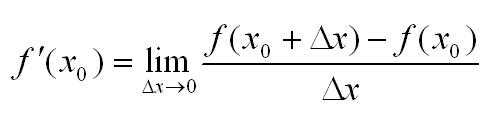
Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

 

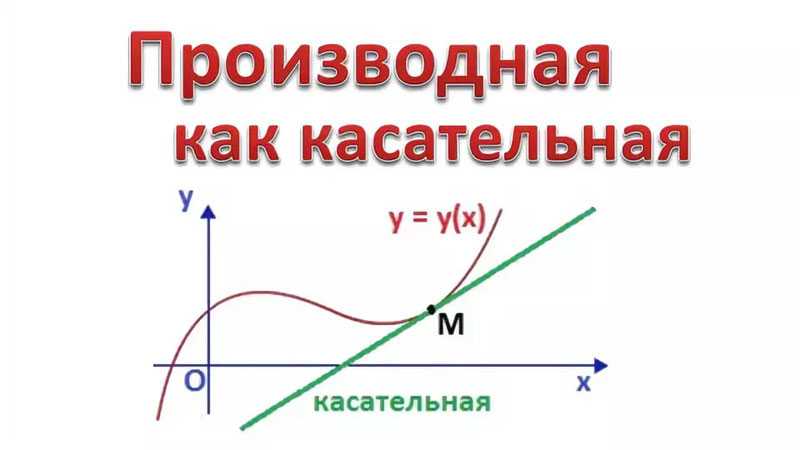
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

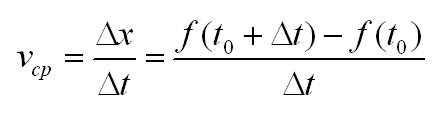
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

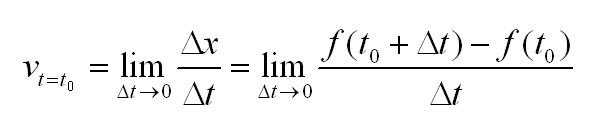
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

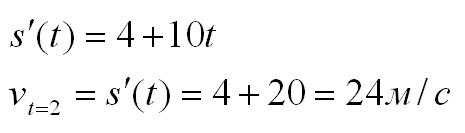
Основные определения

Сложной функцией считается такая функция, у которой аргумент также является функцией.

Обозначается это таким образом: f (g (x)) . Имеем, что функция g (x) считается аргументом f (g (x)) .

Определение 2

Если есть функция f и является функцией котангенса, тогда g (x) = ln x – это функция натурального логарифма. Получаем, что сложная функция f (g (x)) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .

Очевидно, что g (x) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f (f 1 (f 2 (x))) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 (x) = 2 x + 1 x 3 — 5 — дробная рациональная функция.

Определение 3

Степень вложенности определено любым натуральным числом и записывается как y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Определение 4

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

(f (g (x))) » = f » (g (x)) · g » (x)

Алгоритм для сложной функции

Нахождение производной существенно усложняется в том случае, когда функция является сложной. Она состоит из нескольких элементарных выражений. Необходимо находить дифференциал каждой отдельно. Для этой цели пригодятся свойства нахождения производной, каждое из которых следует применять в конкретной ситуации.

Специалисты рекомендуют новичкам воспользоваться некоторым алгоритмом. Он позволяет существенно сократить время и количество вычислений. Решать без алгоритма не рекомендуется, поскольку это можно сделать неверно. Кроме того, необходимо воспользоваться формулами дифференцирования — таблицей производных для их отыскания.

Для сложной функции вида y(g(f(x))) порядок ее дифференцирования следующий:

1. Разбить функцию на составные части.
2. Найти производную f(x) и записать ее вначале.
3. Выполнить дифференцирование g, а затем записать ее после f(x): f'(x) * g'(f(x)).
4. Взять производную y, после этого умножить ее на результат, полученный в пункте 2: f'(x) * g'(f(x)) * y'(g(f(x))).

Принцип очень прост — следует начинать вычислять производную справа налево по частям.

https://youtube.com/watch?v=oAEIPqj4dwc

Например, следует найти дифференциал функции y = (1/2) * sin (2x^2 — 6x).

Для наглядности нужно воспользоваться специальным алгоритмом:

1. Функция имеет вид y = f(g(x)), и состоит из двух частей: g(x) = 2x^2 — 6x и f(x) = sin(g(x)).
2. Производная первого элемента: g'(x) = (2x^2 — 6x)’ = 4x — 6.
3. Дифференциал 2 функции: f'(x) = ‘ = cos(g(x)).
4. Получение результата (можно также упростить выражение при необходимости): y’ = [(1/2) * sin (2x^2 — 6x)]’ = (1/2) * ‘ = (1/2) * (4x — 6) * cos(2x^2 — 6x) = (2x — 3) * cos(2x^2 — 6x).

При решении задачи было задействовано свойство выноса константы за знак дифференциала. Кроме того, функция g(x) — разность двух выражений, производная которых находится по второму свойству дифференцирования. Функция может содержать в своем составе много элементов, но принцип только один.

Следует обратить внимание на первый пункт алгоритма, поскольку нужно правильно разбивать функцию на элементы. На начальной стадии обучения математики рекомендуют воспользоваться онлайн-калькулятором

Он позволяет получить правильное решение. Его можно сравнить результатом, который получен при решении ручным методом.

Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это функция, у которой и степень и основание зависят от «икс»
. Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле .

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера №11.

В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.

Пример 13

Найти производную функции

Используем логарифмическую производную.

В правой части у нас константа и произведение двух множителей – «икса» и «логарифма логарифма икс» (под логарифм вложен еще один логарифм). При дифференцировании константу, как мы помним, лучше сразу вынести за знак производной, чтобы она не мешалась под ногами; и, конечно, применяем знакомое правило :

Как видите, алгоритм применения логарифмической производной не содержит в себе каких-то особых хитростей или уловок, и нахождение производной степенно-показательной функции обычно не связано с «мучениями».

Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — (2 — 3) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .

Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.

Yandex.RTB R-A-339285-1

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения «>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Функция () представляет собой произведение двух элементарных функций, поэтому все просто:

У функции () первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции () представляет собой многочлен, и его производная — это производная суммы. Имеем:

Ответ: ’() =
2 · (3cos − · sin ); ’() = ( + 9) ·
.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию

А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Логарифмическая производная

Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.

Пример 11

Найти производную функции

Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.

Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:

Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:

Собственно приступаем к дифференцированию. Заключаем под штрих обе части:

Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.

Как быть с левой частью?

В левой части у нас сложная функция
. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».

Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ
(если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :

В левой части как по мановению волшебной палочки у нас «нарисовалась» производная . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:

А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:

Окончательный ответ: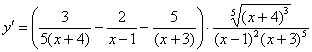

Пример 12

Найти производную функции

Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.

С помощью логарифмической производной можно было решить любой из примеров №№4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.

Алгоритм решения производных

Теорема

Производная функции есть предел отношения приращения этой функции к приращению её аргумента при стремлении последнего к нулю, при условии существования данного предела.

Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.

Процесс нахождения производный называется дифференцированием.

Таблица простых производных

Формулы сложных производных

– производная суммы (разницы).

– производная произведения.

– производная частного.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.