Гипотеза пуанкаре: история проблемы, доказательство, смысл

Доказательство гипотезы

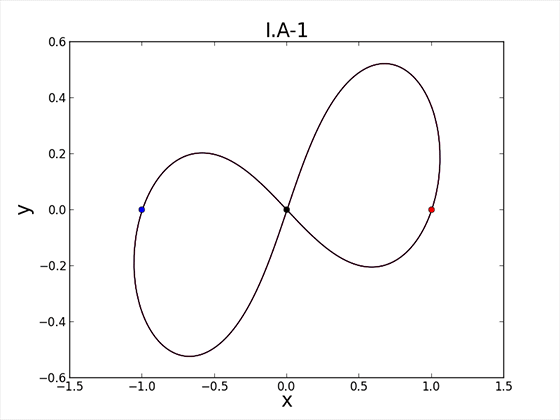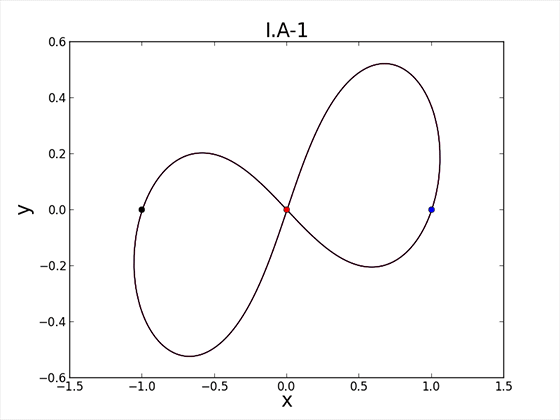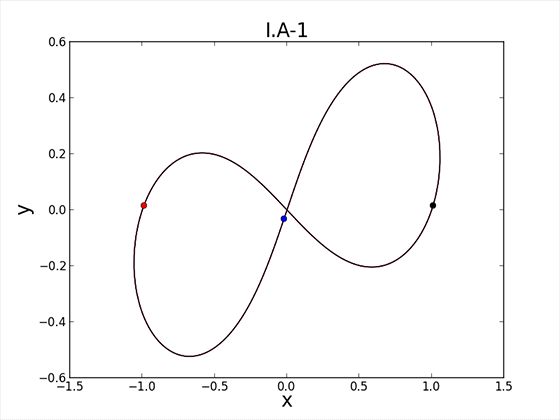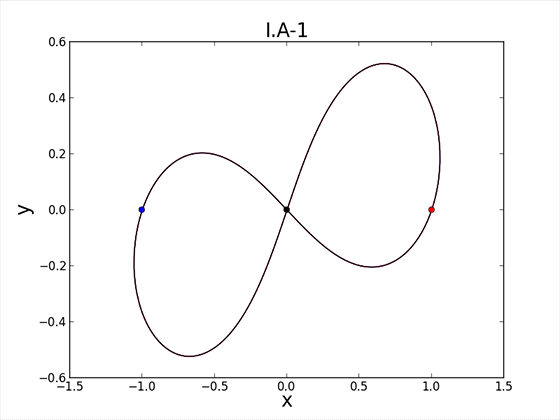
Односвязному трехмерному пространству присваиваются геометрические свойства, оно разделяется на метрические элементы, которые имеют расстояния между собой с образованием углов. Для упрощения берется в качестве образца одномерное многообразие, в котором на эвклидовой плоскости к гладкой замкнутой кривой проводятся в каждой точке касательные вектора, равные 1. При обходе кривой вектор поворачивается с определенной угловой скоростью, равной кривизне. Чем сильнее изгиб линии, тем больше кривизна. Кривизна имеет положительный наклон, если вектор скорости повернут в сторону внутренней части плоскости, которую делит линия, и отрицательный, если повернут вовне. В местах перегиба кривизна равна 0. Теперь каждой точке кривой назначается вектор, перпендикулярный вектору угловой скорости, а длиной равный величине кривизны. Он повернут внутрь, когда кривизна имеет положительный наклон, и вовне – когда отрицательный. Соответствующий вектор определяет направление и скорость, с которой движется каждая точка на плоскости. Если провести в любом месте замкнутую кривую, то при такой эволюции она превратится в окружность. Это справедливо для трехмерного пространства, что и требовалось доказать.

Пример: из воздушного шара при деформации без разрывов можно сделать разные фигуры. Но бублик сделать не получится, для этого его нужно только разрезать. И наоборот, имея бублик, никак не сделаешь цельный шар. Хотя из любой другой поверхности без разрывов при деформации можно получить сферу. Это свидетельствует о том, что эта поверхность гомеоморфна шару. Любой шар можно обвязать ниткой с одним узлом, с бубликом это сделать невозможно.

Шар – это самая простая трехмерная плоскость, которую можно деформировать и свернуть в точку и наоборот.

Важно! Гипотеза Пуанкаре утверждает эквивалентность замкнутого n-мерного многообразия n-мерной сфере в случае его гомеоморфности ей. Она стала отправной точкой в развитии теории о многомерных плоскостях.

2. Схема доказательства

Поток Риччи — это определённое уравнение в частных производных, похожее на уравнение теплопроводности. Он позволяет деформировать риманову метрику на многообразии, но в процессе деформации возможно образование «сингулярностей» — точек, в которых кривизна стремится к бесконечности, и деформацию невозможно продолжить. Основной шаг в доказательстве состоит в классификации таких сингулярностей в трёхмерном ориентированном случае. При подходе к сингулярности поток останавливают и производят «хирургию» — выбрасывают малую связную компоненту или вырезают «шею» (то есть, вложенное ), а полученные две дырки заклеивают двумя шарами так, что метрика полученного многообразия становится достаточно гладкой — после чего продолжают деформацию. Классификация сингулярностей позволяет заключить, что каждый «выброшенный кусок» диффеоморфен сферической пространственной форме. Процесс, описанный выше, называется «поток Риччи с хирургией».

При доказательстве гипотезы Пуанкаре начинают с произвольной римановой метрики на односвязном трёхмерном многообразии M и применяют к нему поток Риччи с хирургией. Важным шагом является доказательство того, что в результате такого процесса «выбрасывается» всё. Это означает, что исходное многообразие M можно представить как набор сферических пространственных форм S3 / Γ_i, соединённых друг с другом трубками . Подсчёт фундаментальной группы показывает, что M диффеоморфно связанной сумме набора пространственных форм S3 / Γ_i и более того все Γ_i тривиальны. Таким образом, M является связной суммой набора сфер, то есть, сферой.

Проблемы анализа пространства (геометрия, топология, теория графов — 4)

Геометрия многомерных пространств и гипотеза Пуанкаре

Над гипотезой о вероятных формах Вселенной бились лучшие умы 20 века.

Решение гипотеза Пуанкаре Григорием Перельманом

Российский математик Григорий Перельман решил гипотезу Пуанкаре.
В 2002-2003 годах он совершил прорыв, предложив ряд новых идей.
Он развил и довел до конца метод, предложенный в 1980-е годы Ричардом Гамильтоном.
В своих работах Перельман утверждает, что построенная им теория позволяет доказать не только гипотезу Пуанкаре,
но и гипотезу геометризации Тёрстона.

Суть метода состоит в том, что для геометрических объектов можно определить некоторое уравнение «плавной эволюции»,
похожее на уравнение ренормализационной группы в теорфизике.
Исходная поверхность в ходе этой эволюции будет деформироваться и, как показал Перельман,
в конце концов плавно перейдет именно в сферу.
Сила этого подхода состоит в том, что, минуя все промежуточные моменты, можно сразу заглянуть «в бесконечность»,
в самый конец эволюции, и обнаружить там сферу.

В  2002 году Г. Перельман опубликовал решение гипотезы Пуанкаре,
и до сих пор ни один пристрастный анализ не нашел в нем ошибки.

Топология и гипотеза Ходжа

Гипотеза Ходжа сформулирована в 1941 году и состоит в том, что для особенно хороших типов пространств,
называемых проективными алгебраическими многообразиями, так называемые циклы Ходжа являются комбинациями объектов,
имеющих геометрическую интерпретацию, — алгебраических циклов.

В XX веке математики изобрели мощные методы исследования формы сложных объектов.
Основная идея состоит в том, чтобы выяснить, до какой степени мы можем аппроксимировать форму данного объекта,
склеивая вместе простые тела возрастающей размерности.
Этот метод оказался эффективным при описании разнообразных объектов встречающихся в математике.
При этом были не ясны геометрические обоснования метода: в некоторых случаях было необходимо прибавлять части,
которые не имели никакого геометрического истолкования.

Доказать гипотезу Ходжа удалось для некоторых частных случаев. Более общее доказательство пока не найдено,
не найдено и доказательство обратного — что гипотеза неверна.

Проблемы 2000 года: гипотеза Ходжа.

Квантовая физика и геометрия (гипотеза Янга-Миллса)

Тео́рия Я́нга—Ми́ллса — калибровочная теория с неабелевой калибровочной группой.
Калибровочные поля в этой теории называются полями Янга — Миллса.
Такие теории были предложены в 1954 году Чж. Янгом (Yang) и Р. Миллсом (Mills),
однако долгое время рассматривались лишь как математические изыски, не имеющие отношения к реальности.

Несмотря на это, именно на основе теорий Янга — Миллса в 1970-х годах были созданы
две краеугольные теории Стандартной Модели в физике элементарных частиц:
квантовая хромодинамика (теория сильных взаимодействий) на основе группы SU(3)
и теория электрослабых взаимодействий на основе группы SU(2).

Теория Янга-Миллса.

Теория графов и теорема Шварца-Кристоффеля

Теорема Шварца — Кристоффеля относится к теории функций комплексного переменного
и носит название немецких математиков Карла Шварца и Элвина Кристоффеля.

Она касается проблемы о конформном отображении некой канонической области (единичного круга Δ или верхней полуплоскости H+)
на внутренность произвольного многоугольника

Теорема дает общий вид таких отображений, что важно с практической точки зрения.. Сформулированная 140 лет назад формула Шварца–Кристоффеля является незаменимой для проектирования различных объектов,
включая здания, мосты, а также самолеты

Она определяет уровень внешней и внутренней сопротивляемости структуры и степень запаса ее прочности. Однако классическая формула не могла быть применена для сложных объектов, имеющих отверстия и сложные формы

Сформулированная 140 лет назад формула Шварца–Кристоффеля является незаменимой для проектирования различных объектов,
включая здания, мосты, а также самолеты.
Она определяет уровень внешней и внутренней сопротивляемости структуры и степень запаса ее прочности.
Однако классическая формула не могла быть применена для сложных объектов, имеющих отверстия и сложные формы.

• Доказательства великих завихрений.

Верное направление

Григорий Яковлевич отмечает, что его всегда увлекали сложные проблемы, такие как теорема Пуанкаре. Доказательство Перельман стал искать в направлении, вынесенном из беседы с профессором Колумбийского университета Ричардом Гамильтоном (род. 1943). Во время пребывания в США он специально ездил из другого города на лекции этого неординарного ученого. Перельман отмечает прекрасное доброжелательное отношение профессора к молодому математику из России. В их разговоре Гамильтон упомянул о потоках Риччи – системе дифференциальных уравнений – как способе решения теорем геометризации.

Гамильтон пришел в тупик, когда увидел, что при преобразованиях кривых под действием потоков Риччи образуются сингулярные (обращающиеся в бесконечность) зоны, которые не предусматривала теорема Пуанкаре. Простыми словами, Перельману удалось нейтрализовать образование таких зон, и многообразие благополучно превратилось в сферу.

Институт Клэйя

Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.

В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.

Ошибка на ошибке: история вопроса

Все началось с исследований, которые Пуанкаре вел в области алгебраической геометрии. Он работал над одним из краеугольных камней этой науки — теорией гомологий, особого класса топологических инвариантов. В 1900 году он опубликовал статью, в которой доказывал, что если у трехмерной поверхности гомология совпадает с гомологией сферы, то и сама поверхность — сфера; на самом деле это утверждение даже более сильное, чем утверждение гипотезы Пуанкаре.

Однако в его рассуждения вкралась ошибка, которую он сам и нашел, к 1904 году разработав важнейшее понятие фундаментальной группы и построив на его базе контрпример к собственной теореме. Тогда же он наконец-то поставил вопрос правильно.

Достаточно долго на гипотезу не обращали внимания. Интерес к ней пробудил Генри Уайтхед, который в 1930-е годы объявил о том, что нашел доказательство. Как вы уже догадались, его доказательство также было неверным. Однако в процессе поиска и попыток исправить свои неточности он обнаружил интереснейшие классы трехмерных поверхностей и значительно продвинул теорию, которая позднее получила название топологии малых (или низших) размерностей. В пятидесятые и шестидесятые годы всплеск интереса к проблеме вновь породил несколько ошибочных заявлений о том, что теорему удалось доказать, и после этого математики наконец-то поняли, что гипотезу Пуанкаре так просто не возьмешь: с шестидесятых годов и до работ Григория Перельмана ложные доказательства предъявляли только любители (таких всегда достаточно; не присоединяйтесь к их числу).

Топология низших размерностей стала отдельной ветвью математики по удивительной причине — в многомерном случае все гораздо проще! Уже в 50-е и 60-е годы утверждения, аналогичные гипотезе Пуанкаре, были доказаны для более высоких размерностей. Трехмерный же случай продолжал оставаться камнем преткновения.

Доказательство Григория Перельмана (см. врезку) основано на идеях, которые развил в начале 1980-х годов Ричард Гамильтон (Richard Hamilton). Эти идеи неожиданным образом выводят топологические заключения из фактов о дифференциальных уравнениях — так называемых потоках Риччи (Ricci flows), обобщающих уравнения термодинамики. Впрочем, в доказательстве Перельмана долгое время не могли разобраться ведущие топологи мира, и вряд ли оно когда-нибудь станет темой популярной статьи.

Проблемы движения тел и среды (1-2)

Обьявленные здесь проблемы динамики дискретных тел и непрерывной среды — фактически,
физические, но сводимые к математическим формулам.

Уравнение Навье-Стокса

Среди 7 проблем тысячелетия 6-я проблема является чисто прикладной задачей.
От ее решения зависит качество проектирования самолетов, ракет, снарядов, гидротурбин, подводных лодок, газо- и нефтепроводов.
В биологии и медицине решение этого уравнения дает всю правду о течении крови в сосудах, жидкости в клетках сосудов и т.д.

Решить уравнения Навье-Стокса не могут с 1822 года. Более того, не могут доказать: правильно ли мы решаем это уравнение,
а их приходится решать на компьютерах в силу большой размерности, где 3 — уже много.

Поэтому, прежде, чем вычислять, надо доказать теорему существования и единственности решения (СЕР),
что составляет суть проблемы и важно потому, что аварии на газопроводах, гидростанциях, авиакатастрофы
могут оказаться следствием неправильных расчетов уравнения Навье-Стокса, а не слепой случайности. (Чоро Тукембаев)

(Чоро Тукембаев)

Исследователи, занимавшиеся или занимающиеся УНС, внёсшие свой вклад или взгляд в решение этого типа уравнений; их работы:

• Американка Пенелопа Смит (Penelope Smith) из Университета Лихай (Lehigh University, Вифлеем, штат Пенсильвания)
  опубликовала 26.09.2006 сатью «Immortal Smooth Solution of the Three Space Dimensional Navier-Stokes System«.
  Она выяснила, что уравнения Навье-Стокса могут быть перезаписаны в форме дифференциальных уравнений,
  которые она знала, как решать. В статье представлено это решение и она уверена в нём.
  Смит когда-то также посещала те же самые семинары, что и наш Григорий Перельман.
• Большой вклад в развитие теории уравнений Навье-Стокса внесла некогда
  и наша петербургская женщина-математик Ольга Ладыженская.
  Главным результатом Ладыженской в этой области стало полное решение проблемы в двумерном случае.

• Статьи Чоро Тукембаева:
• Работы Талайбека Омурова, Кыргызстан:
• Работы Намаза Алтаева (Казахстан, г.Шымкент):

  Намаз считает, что принятые подходы к решению уравнений Эйлера и Навье-Стокса методами математической физики ведут в тупик.
  Он полагает, что природу этих уравнений можно удовлетворительно интерпретировать,
  если за основу анализа брать основополагающие принципы теоретической и эмпирической физики.

Задача притяжения трех тел

Задача о движении трех материальных точек под действием ньютоновских сил взаимного притяжения — «задача трех тел» — получила в математике, механике и астрономии широкую известность. Достаточно просмотреть посвященные этой задаче главы в книгах Уиттекера, Биркгофа, Зигеля и статьи Арнольда и Смейла, чтобы убедиться в богатстве и плодотворности круга идей, так или иначе обязанных ей своим возникновением. Задача трех тел описывается системой дифференциальных уравнений; ей соответствует фазовый поток в 18-мерном фазовом пространстве.

Пояснения

Многообразие

Трехмерное многообразие — это то, что выглядит как трехмерное евклидово пространство в окрестности каждой точки на многообразии .

Закрыто

В этом контексте замкнутое означает, что многообразие компактно (то есть не расширяется в бесконечность) и что у него нет границы . Трехмерная сфера — это примерно трехмерное многообразие, но у нее есть край (поверхность). Поэтому он не закрыт. С другой стороны, его поверхность представляет собой замкнутое двумерное многообразие. Гипотеза Пуанкаре делает только одно утверждение для замкнутых многообразий.

Просто подключено

Односвязность означает, что любую замкнутую кривую можно свернуть в одну точку. Резинку на сферической поверхности всегда можно двигать по поверхности так, чтобы она превратилась в точку. На торе (например , велосипед трубки), например, сокращение не всегда работает: Если резиновая лента проходит вокруг боковой тоньше велосипедной трубки, он никогда не может быть стянуты в точку (вы должны сократить трубка, что недопустимо в топологии). Следовательно, тор не односвязен.

3 сфера

В общем случае n-сфера (обозначение — это край (n + 1) -мерной сферы . 1-сфера — это круговая линия круглой области . 2-сфера — это поверхность трехмерной сферы. Трехмерная сфера — это поверхность четырехмерной сферы. Этот объект, конечно, уже нельзя просто вообразить, потому что он на самом деле «живет» в четырехмерном пространстве. Математически 3-сферу можно легко описать формулой, а именно как набор всех точек в 4-мерном реальном пространстве, которые находятся на расстоянии 1 от нулевой точки:
С.п{\ Displaystyle S ^ {п}}

С.3знак равно{(Икс1,Икс2,Икс3,Икс4-й)|Икс12+Икс22+Икс32+Икс4-й2знак равно1}{\ Displaystyle S ^ {3} = \ {(x_ {1}, x_ {2}, x_ {3}, x_ {4}) | x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} + x_ {4} ^ {2} = 1 \}}

2-сфера состоит из двух (полых) полусфер, соединенных по краям. Топологически эти полые полусферы на самом деле являются круглыми поверхностями (если вы прижмете их сверху, образуются два диска). С его помощью вы можете получить 2 сферы, склеив две круглые области по краям. Таким же образом можно построить относительно четкую картину трехмерной сферы. Вы берете две сферы (соответствует круглым областям в 2-мерном пространстве) и «склеиваете» их вместе в соответствующих точках на поверхности. Таким образом, путь на 3-й сфере начинается в одной из двух сфер. Когда вы добираетесь до края, вы перепрыгиваете в соответствующую точку на втором шаре и наоборот. Таким образом можно описывать пути на трехмерной сфере в трехмерном пространстве. Вы также можете увидеть, что здесь нет края. Таким образом, 3-сфера замкнута.

Доказательство

Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.

В 1930-х годах интерес к гипотезе вернулся. Прежде всего, формулировка была расширена до «n-мерного пространства», а потом американец Уайтхед сообщил об успешном доказательстве, позднее отказавшись от него. В 60-70-х сразу два математика — Смейл и Столлингс — практически одновременно, но разными способами разработали решение для всех n больше 4.

В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.

Дальше работа несколько застопорилась — американец Ричард Гамильтон предложил использовать в решении поток Риччи, но столкнулся с трудностями и не завершил исследования.

На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили «до блеска» американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.

Исторический

Формулировка

Вопрос был впервые задан Анри Пуанкаре в 1904 году и гласил:

Каждые 3-многообразие компактного без краев и односвязный является его гомеоморфно к 3-сфере  ?

Пуанкаре с большой проницательностью добавил комментарий: «Но этот вопрос завел бы нас слишком далеко» .

Чаще всего , речь идет об определении того , в  данном « трехмерный одномерном объекте » , имеющая то же свойство , как 3D — сфере (в частности , все контуры могут быть «затянуты» на точке ) действительно только деформация из ‘ трехмерная сфера ( обычная сфера — поверхность в обычном пространстве — имеет только два измерения).

Никакое безграничное 3-многообразие, кроме ( обычного , неуплотненного пространства), не может быть чисто нарисовано как объект в обычном трехмерном пространстве. Это одна из причин, почему трудно мысленно представить себе содержание гипотезы.
р3{\ Displaystyle \ mathbb {R} ^ {3}}

Недавний прогресс

К концу 2002 года публикации по Arxiv по Перельман из Математического института в Санкт — Петербурге свидетельствуют о том , что он , возможно, нашли доказательство «  гипотезы геометризации  » (см ), осуществление программы было описано ранее на Ричарда С. Гамильтон . В 2003 году он опубликовал второй отчет и прочитал серию лекций в США . В 2006 году эксперты пришли к выводу, что недавняя работа Перельмана в 2003 году решила эту проблему, почти через столетие после его первого заявления. Это признание было официально объявлено на Международном математическом конгрессе 22 августа 2006 г. в Мадриде , во время которого он был награжден медалью Филдса совместно с тремя другими математиками. Однако Перельман отказался от медали и намекнул, что откажется и от премии Клея . Эта премия была вручена ему 18 марта 2010 года вместе с призом в миллион долларов, и он фактически отказался от нее. По словам Александра Забровского , который утверждает, что получил от него интервью, 29 апреля года он сказал газете « Комсомольская правда »  :

«Почему мне потребовалось столько лет, чтобы решить гипотезу Пуанкаре?» Я научился обнаруживать пустоты. Вместе с моими коллегами мы изучаем механизмы заполнения социальных и экономических пробелов. Везде пустоты. Мы можем их обнаружить, и это дает много возможностей … Я знаю, как управлять Вселенной. Тогда скажи мне, какой смысл гоняться за миллионом долларов? «

Но это утверждение Забровского является спорным, поскольку несколько журналистов отрицают подлинность этого интервью.

Появление топологии

В 19-20 столетии появилась еще одна наука, которая вышла из геометрии — топология. Именно она и определила дальнейшее развитие математики в 20 столетии. Топология включила в себя основные фундаментальные структуры геометрического типа, которые имеют прямое отношение к физике прошлого века. Больше всего труда в этот процесс вложил Анри Пуанкаре, французский математик, который мог не только выделить основные топологические структуры, но при этом еще и создал специальный язык, с помощью которого их описал.

Если рассматривать, какая именно разница присутствует между топологией и геометрией, то можно сказать, что во второй более важную роль играет расстояние. Есть две точки и между ними определенное расстояние, которое необходимо знать, чтобы получить правильный ответ. Когда речь идет о топологии, то сразу же возникает вопрос относительно того, есть ли вообще шансы на то, что получится преодолеть данное расстояние между двумя точками, где именно находятся эти точки. Топология предполагает использование более простых и понятных вопросов, чем геометрия. Они, как правило, находятся в основе всего, что люди обычно используют для подробного описания окружающей среды.

история

Первоначально Пуанкаре выдвинул несколько иную гипотезу: он считал, что каждое трехмерное замкнутое многообразие, имеющее те же гомологии, что и трехмерная сфера, уже должно быть топологически сферой. В то время как Пуанкаре первоначально полагал, что у него есть доказательство, основанное на этом более слабом предположении, требование односвязности многообразия оказалось необходимым. С гомологической сферой Пуанкаре сам Пуанкаре нашел контрпример к своей исходной гипотезе: она имеет те же гомологии, что и 3-сфера, но не односвязна и, следовательно, не может быть гомотопически эквивалентна 3-сфере. Поэтому он изменил свое предположение на известное сегодня заявление.

Интересно, что n-мерная гипотеза Пуанкаре имеет очень разные доказательства в разных измерениях, а формулировка является общей.

Ибо постановка считается классической; в этом случае известны и классифицированы даже все (замкнутые) двумерные многообразия .
пзнак равно2{\ displaystyle n = 2}

В этом случае гипотеза Стивена Смейла была доказана в 1960 году (для гладких и PL-многообразий) с использованием техники теории Морса . Это следует из его теоремы о H-кобордизме . За это доказательство, среди прочего, он получил медаль Филдса в 1966 году . Позже Макс Ньюман распространил свои аргументы на топологические многообразия.
п>4-й{\ displaystyle n> 4}

Майкл Фридман раскрыл дело в 1982 году. Он также получил за это медаль Филдса в 1986 году .
пзнак равно4-й{\ displaystyle n = 4}

Случай оказался (что неудивительно) самым сложным. Многие математики представили доказательства, но они оказались ложными. Тем не менее, некоторые из этих ошибочных свидетельств расширили наше понимание низкоразмерной топологии.
пзнак равно3{\ displaystyle n = 3}

Кто такой Анри Пуанкаре

Жюль Анри Пуанкаре (фр. Jules Henri Poincaré) родился 29 апреля 1854 в Нанси, Франция, а умер 17 июля 1912 в Париже, Франция. Он был французским ученым, в сферу интересов которого входили самые разные науки. Среди них были: математика, механика, физика, астрономия и философия.

Кроме того, что он занимался исследованиями, Анри Пуанкаре в разные годы также был главой Парижской академии наук, членом Французской академии и ещё более 30 академий мира, в том числе иностранным членом-корреспондентом Петербургской академии наук.

Чуть ли не единогласно историки называют Анри Пуанкаре одним из величайших математиков всех времён. Его ставили в один ряд с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени.

Анри Пуанкаре сделал для математики настолько много, что некотрые его труды до сих пор приносят нам пользу.

Перу Анри Пуанкаре принадлежат более 500 статей и книг. Все это говорит о нем, как о гении, который даже спустя более 100 лет после своей смерти может изменить мир будущего своими теориями, формулами, рассуждениями и прочими научными трудами.

3. История

Обложка журнала Science № 314(5807), 2006 год, провозглашающая доказательство гипотезы Пуанкаре «прорывом года».

В 1900 году Пуанкаре сделал предположение, что трёхмерное многообразие со всеми группами гомологий как у сферы гомеоморфно сфере. В 1904 году он же нашёл контр-пример, называемый теперь сферой Пуанкаре, и сформулировал окончательный вариант своей гипотезы. Попытки доказать гипотезу Пуанкаре привели к многочисленным продвижениям в топологии многообразий.

Доказательства обобщённой гипотезы Пуанкаре для n ⩾ 5 получены в начале 1960—1970-х почти одновременно Смейлом, независимо и другими методами Столлингсом (англ.) (для n ⩾ 7, его доказательство было распространено на случаи n = 5 и 6 Зееманом (англ.)). Доказательство значительно более трудного случая n = 4 было получено только в 1982 году Фридманом. Из теоремы Новикова о топологической инвариантности характеристических классов Понтрягина следует, что существуют гомотопически эквивалентные, но не гомеоморфные многообразия в высоких размерностях.

Доказательство исходной гипотезы Пуанкаре (и более общей гипотезы Тёрстона (англ.)) было найдено только в 2002 году Г. Я. Перельманом. Впоследствии доказательство Перельмана было проверено и представлено в развёрнутом виде как минимум тремя группами учёных. Доказательство использует поток Риччи с хирургией и во многом следует плану, намеченному Гамильтоном (англ.), который также первым применил поток Риччи.

3.1. Признание и оценки

• Фридман (в 1986 году) и Перельман (в 2006 году) стали Филдсовскими лауреатами.
• В 2006 году журнал Science назвал доказательство Перельманом гипотезы Пуанкаре научным «прорывом года» («Breakthrough of the Year»). Это первая работа по математике, заслужившая такое звание.
• В 2006 году Сильвия Назар опубликовала нашумевшую статью «Manifold Destiny», которая рассказывает об истории доказательства гипотезы Пуанкаре.
• 18 марта 2010 года математический институт Клэя присудил Премию тысячелетия за доказательство гипотезы Пуанкаре Г. Я. Перельману, который, однако, отказался её принять.

Алгоритмическая версия

К теме этой статьи примыкает интересная для компьютерщиков область математики — вычислительная топология. Вычислительные и распознавательные задачи есть, оказывается, и в этой абстрактной науке. С одной из таких задач связана и предпринятая в 1974 году очень интересная попытка решения проблемы Пуанкаре в ее алгоритмической версии.

Каждая трехмерная поверхность задается некоторым (не будем вдаваться в подробности) дискретным кодом — конечным набором символов. Одна и та же поверхность имеет бесконечное число различных кодировок. Естественный вопрос: существует ли алгоритм, определяющий по заданному кодовому слову, задает ли оно трехмерную сферу («алгоритмическая проблема Пуанкаре»). Именно эту задачу атаковали в 1974 году А. Фоменко (тот самый), И. Володин и В. Кузнецов . Они предположили, что определенное свойство кода (оно было названо «волной») дает критерий «сферичности». Однако строго доказать им удалось только, что наличие «волны» гарантирует — перед нами сфера. Доказать же, что в любом коде, задающем сферу, имеется «волна» никак не получалось. Тогда авторы сделали весьма стильный по тем временам ход — провели масштабный компьютерный эксперимент. Была написана программа для машины БЭСМ-6, которая случайным образом генерировала коды, задающие трехмерную сферу, и проверяла наличие в них «волны». В эксперименте, потребовавшем весьма длительного счета, был проверен миллион таких случайных представлений сферы — и во всех обнаружилась волна! С точки зрения здравого смысла — веский аргумент в пользу корректности предложенного алгоритма. Но авторы, будучи серьезными математиками, разумеется, воздерживались от поспешных заявлений. И не напрасно — спустя пару лет один из бывших учеников Фоменко обнаружил контрпример…

Спустя двадцать лет алгоритм распознавания 3-сферы (за экспоненциальное время) был построен. Общая же проблема алгоритмического распознавания поверхностей размерности 3 открыта, она активно изучается и сегодня. Для более высоких размерностей давно известна ее неразрешимость, для размерности 2 она была решена еще раньше, а вот в нашем родном трехмерье все почему-то невероятно сложно устроено.Леонид Левкович-Маслюк