Формулы прямоугольника, формулы для расчета площади и периметра прямоугольника

Периметр прямоугольника

Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.

Периметр прямоугольника — это сумма длин всех его ребер.

Основные свойства прямоугольника:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

противоположные стороны фигуры равны и параллельны друг другу;
сумма всех углов равна 360 градусов;
диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
диагонали делят фигуру на два одинаковых прямоугольных треугольника;
по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
стороны рассматриваемого четырехугольника также являются его высотами;
точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
диагональ этого четырехугольника — это диаметр описанной окружности;
вокруг него всегда можно описать окружность.

Примеры решения задач

Задача 1

Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.

Решение:

Применяем самую первую формулу для расчета:

$P=2(a+b)$

Получается:

$P=2(5+7)=24$ см

Ответ: 24 см.

Задача 2

Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 $см^2$, одна из его сторон равна 6 см. Вычислить Р фигуры.

Решение:

Берем формулу $P=2(\frac Sa+a)$ и подставляем известные значения:

$P=2(\frac{24}6+6)=2\times10=20$ см

Ответ: 20 см.

Задача 3

Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.

Решение:

Вспоминаем формулу для расчета $P=2(a+\sqrt{d^2-a^2})$ и вставляем известные величины:

$P=2\;(3+\sqrt{5^2-3^2})=2(3+\sqrt{25-9})=2\times7=14$ см

Ответ: 14 см.

Задача 4

Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.

Решение:

В этом случае для расчета суммы длин всех сторон применяем формулу $P=2(a+\sqrt{4R^2-a^2})$. Используем известные значения и получаем:

$P=2\;(3+\sqrt{4\times5^2-3^2})=2(3+\sqrt{100-9})=2(3+\sqrt{91})=6+2\sqrt{91}$ см.

Прямоугольник и тригонометрические функции

Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.

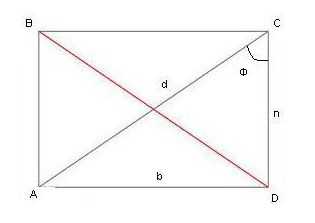
Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.

Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.

Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.

√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.

Периметр равен 2(17,3+10)=2*27,3=54,6 см.

Что такое периметр квадрата

Слово периметр пришло из древности и например древние-греческом обозначала окружность(περίμετρον).

Или если совсем по простому — периметр квадрата это — сумма всех границ.

Периметр квадрата это сумма всех сторон квадрата, поскольку их 4 одинаковых, то одну сторону, надо умножить на 4.

Формула периметра квадрата — периметр квадрата равен стороне умноженной на 4 -> P=4a

Где P — периметр квадрата,

a — длина одной из сторон.

Как мы уже говорили выше у нас есть формула нахождения периметра :

найдите периметр квадрата, если сторона квадрата равна 12 см.

Сторона квадрата это а, она равна 12см.

Подставляем 12 в формулу вместо буквы «а».

P = 4a -> P = 4 * 12-> P = 48см.

Если сторона квадрата равна 12 см, то периметр квадрата равен 48см.

найдите периметр квадрата, если площадь квадрата равна 25см².

Опять вспоминаем формулу площади квадрата :

Из этой формулы нам требуется вывести сторону :

Далее берем формулу периметра квадрата и заменяем сторону на корень квадратный.

Извлекаем корень из 25 на калькуляторе

После этого умножаем на 4 :

Если площадь квадрата 25см², то периметр будет равен 20см.

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

Первый способ вычисления периметра квадрата

Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

где: P — периметр квадрата a — длина стороны квадрата

Второй способ вычисления периметра квадрата

Периметр квадрата равен произведению длины его диагонали на два корня из двух.

где: P — периметр квадрата a — длина стороны квадрата d — длина диагонали квадрата

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Математика
Информатика
Финансы
Жизнь
Здоровье

Работа с текстом
Работа с цветом
Конвертеры
Графики

Алгебра
Геометрия
Тригонометрия
Физика
Химия
Литература
Информатика
Астрономия
Законы
Единицы измерений
Таблицы
Инструкции

Знаменитые химики
Знаменитые физики
Знаменитые математики
Знаменитые биологи
Знаменитые психологи
Знаменитые философы

ЕГЭ
Гаджеты
Разное

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX. Поэтому для корректного отображения формул и выражений пожалуйста дождитесь полной загрузки страницы.

Пользовательское соглашение
Cookie
О сайте

2021 Все калькуляторы online

Копирование материалов запрещено

Используя этот онлайн калькулятор, вы сможете найти периметр квадрата.

Воспользовавшись онлайн калькулятором для вычисления периметра квадрата, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

квадрата:

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = aba = 6, b = 2S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = abS = 12, a = 6, b = x12 = 6 × xx = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2a = 8S = 82 = 64 см2Ответ: площадь квадрата со стороной 8 см равна 64 см2

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abca = 6, b = 4, c = 3V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abcV = 200, a = 10, b = 5, c = x200 = 10 × 5 × x200 = 50xx = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.

Решение

a — длинаb — ширинаc — высота

a = 42 мb = мc = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525a = 5.8b = 3.5c = x

35,525 = 5,8 × 3,5 × x35,525 = 20,3 × xx = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.

Рассмотрим пример:по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Рис. 1. Земельный участок формой прямоугольника.

Земельный участок имеет стороны длиной 2 м, 4 м, 2 м, 4 м. Поэтому чтобы узнать общую длину забора необходимо сложить длины всех его сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют латинскую букву P.

Для вычисления периметра произвольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в различных единицах длины: мм, см, м, км и так далее. При необходимости, данные в задании, переводят в одинаковые единицы измерения.

Основные понятия

Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:

Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
Квадрат. Является четырехугольником, все стороны которого равны.

При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

: a 2 + b 2 = c 2
, где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник
  — это четырехугольник со всеми прямыми углами.
- Квадрат
  — прямоугольник, у которого все стороны равны.
Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Не многие формулы из курса школьной математики мы применяем в повседневной жизни. Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Что такое прямоугольник и квадрат

Прямоугольник
– это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат
– это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

A, B, C, D

Пример.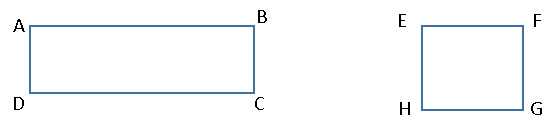
Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника

Периметр обозначается латинской буквой P
. Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P
ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.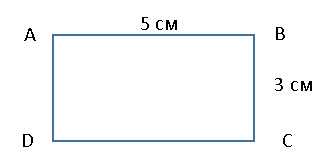
2. Напишем формулу для расчета периметра данного прямоугольника:

P
ABCD = 2 * (AB + BС)

P
ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Формула расчета периметра квадрата

P
ABCD = 2 * (AB + BC)

P
ABCD = 4 * AB

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P
ABCD = 4 * AB

P
ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев. Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь
S

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S
AKMO = AK * KM

S
AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S
AВСО = AB * BC = AB * AB

S
AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр
— это сумма длин всех сторон многоугольника.

Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

Прямоугольник – это четырехугольник.
Все параллельные стороны равны
Все углы = 90º.
Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Формула периметра фигуры

Если принять во внимание тот факт, что противоположные стороны прямоугольника равны, то можно вывести формулу периметра прямоугольника:

$P = (a+b) * 2$, где а, b – стороны фигуры.

Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.

Существует и другой способ найти периметр. Если в задании даны лишь одна сторона прямоугольника и площадь фигуры, можно выразить другую сторону через его площадь. Тогда формула будет выглядеть следующим образом:

$P = {{2S + 2a^2}\over{a}}$, где S – площадь прямоугольника.

Рис. 3. Прямоугольник со сторонами a, b .

Задание: Вычислить периметр прямоугольника, если его стороны равны 4 см и 6 см.

Решение:

Используем формулу $P = (a+b)*2$

$P = (4+6)*2=20 см$

Таким образом, периметр фигуры $P = 20 см$.

Так как периметр – это сумма всех сторон четырёхугольника, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.

Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.

Что мы узнали?

Мы узнали, как найти периметр прямоугольника. А также ознакомились с формулой его вычисления. С этой темой можно столкнуться не только при решении математических задач, но и в реальной жизни.

/5

Вопрос 1 из 5

Варианты нахождения периметра прямоугольника

По сторонам

Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:

$P=2(a+b)$

где $a$ и $b$ — это две соседние стороны фигуры.

По любой стороне и площади

Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.

Так как площадь прямоугольника — это произведение двух его смежных сторон $(S=a\times b)$, чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: $b=\frac Sa$.

Получается, что формула для расчета $P$ рассматриваемой фигуры будет выглядеть следующим образом:

$P=2(\frac Sa+a)$

По любой стороне и диагонали

В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.

$b=\sqrt{d^2-a^2}$

где $d$ — диагональ прямоугольника, а $b$ — неизвестная сторона.

Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:

$P=2(a+\sqrt{d^2-a^2})$

По любой стороне и радиусу описанной окружности

Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:

$b=\sqrt{4R^2-a^2}$

где $R$ — радиус описанной окружности.

Тогда формула для расчета P будет выглядеть так:

$P=2(a+\sqrt{4R^2-a^2})$

Примеры решения задач

Задача 1

Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.

Решение:

Применяем самую первую формулу для расчета:

Задача 2

Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 $см^2$ , одна из его сторон равна 6 см. Вычислить Р фигуры.

Решение:

Берем формулу $P=2(\frac Sa+a)$ и подставляем известные значения:

Задача 3

Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.

Решение:

Вспоминаем формулу для расчета $P=2(a+\sqrt)$ и вставляем известные величины:

Задача 4

Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.

Решение:

В этом случае для расчета суммы длин всех сторон применяем формулу $P=2(a+\sqrt)$ . Используем известные значения и получаем:

Источник

Примеры задач

Условие первой.
Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.Решение.
Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см. Ответ.
Периметр треугольника равен 12 см.

Условие второй.
Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.Решение
. Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.Ответ.
Периметр равняется 37 см.

Условие третьей.
Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.Решение.
Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см. Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.Ответ.
Сторона квадрата 4 см.

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами . Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:

3 а = 100 м2 × 3 = 300 м2

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:

1 сотка = 100 м2

2 сотки = 200 м2

10 соток = 1000 м2

Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:

20 га = 10 000 м2 × 20 = 200 000 м2

Свойства прямоугольника

Рассмотрим чем отличается прямоугольник от других фигур.

1. В прямоугольнике противоположные стороны равны.

2. Уровни между собой и имеют 90 градусов все углы прямоугольника.

3. Диагонали прямоугольника равны и в точке пересечения делятся пополам.

4. Диагонали треугольника делят его на два одинаковых треугольника.

Таким образом, если в параллелограмме все углы ровны или один прямой, или одинаковые диагонали то это прямоугольник. Что касается четырехугольников, то среди них прямоугольниками будут только те, у которых все углы равны или хотя бы три прямые. Биссектриса угла прямоугольника отсекает от него равнобедренный треугольник.

Основными геометрическими характеристиками прямоугольника является периметр и площадь.

Измерительные приборы на местности

Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант – это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.

Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.

Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L
– длина окружности

π
– это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» — лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π =
3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R
— это радиус окружности

D
– Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L
= 2*3,14*3

L
=6
π

L=6*3.14

L
= 18.84 см

P
к
= 18,84 см

Ответ: 18.84 см

Как найти периметр обычного прямоугольника

Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:

Складываем все стороны.

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.

Решение (последовательность действий и рассуждения):

Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Ответ: P = 18 см.

Второй способ заключается в следующем:

Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.

В рамках данной задачи получим такое решение:

2×(3 + 6) = 2×9 = 18.

Ответ: P = 18.

Как найти периметр прямоугольника, зная его площадь?

этого не достаточно. Надо еще знать одну из сторон

Ни по какой. Вариантов будет бесконечное множество

Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом.
Свойства прямоугольника
противолежащие стороны равны и параллельны друг другу;
диагонали равны и в точке пересечения делятся пополам;
сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон.
Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(a + b).
Длина диагонали d прямоугольника вычисляется по теореме Пифагора:
d = √(a2 + b2).
Углы между диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу:
S = a·b.
Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними:
S = d2·sin(α/2)·cos(α/2).
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
R = √(a2 + b2)/2.
В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.

решить систему уравнений
одно из которых — формула площади второе формула периметра

периметер p=2*a+(2*s)/a, где а от 0 до s

надо решить систему уравнений например если пл-дь равна 16, то ситема примет вид. при учете что х это периметр, а и в стороны прямоугольника, то
а*в=16
2а+2в=х
отсюда верхнее уравнее системы можно выразить одну сторну через другую и подставить в нижнее уравнение, например:
а=16/в
то
2(16/в) +2в=х
вот только надо знать сторону хоть одну чтобы определить вторую, а строна в как как писал выше Aqni имеет значения почти от нуля и почти до S внашем почти до 16….пиши мне на мыло если не понятно до сих пор )

Встречный вопрос — в доме 40 квартир — сколько это этажей?
— емкость в 1 литр — какой диаметр емкости?
Продолжить?…

S=a*b=к примеру 45см ^2
разложим на простые множители 45
45/3=15
15/3=5
5/5=1
НОД=1
Р=2(3^2+5^1)=2(9+5)=28
P.S. Как разложить число на простые множители см. <a rel=»nofollow» href=»https://otvet.mail.ru/question/14487466″ target=»_blank»>https://otvet.mail.ru/question/14487466</a>

Чтобы найти периметр прямоугольника надо сложить все его стороны.

плюс минус при подборе вручную по формуле будет иногда разницы втрое

Периметр треугольника

Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.

Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.

Читать еще: Тест нарисовать дом дерево человека расшифровка пример. Методика исследования личности «Дом-дерево-человек» Дж