Многоугольники

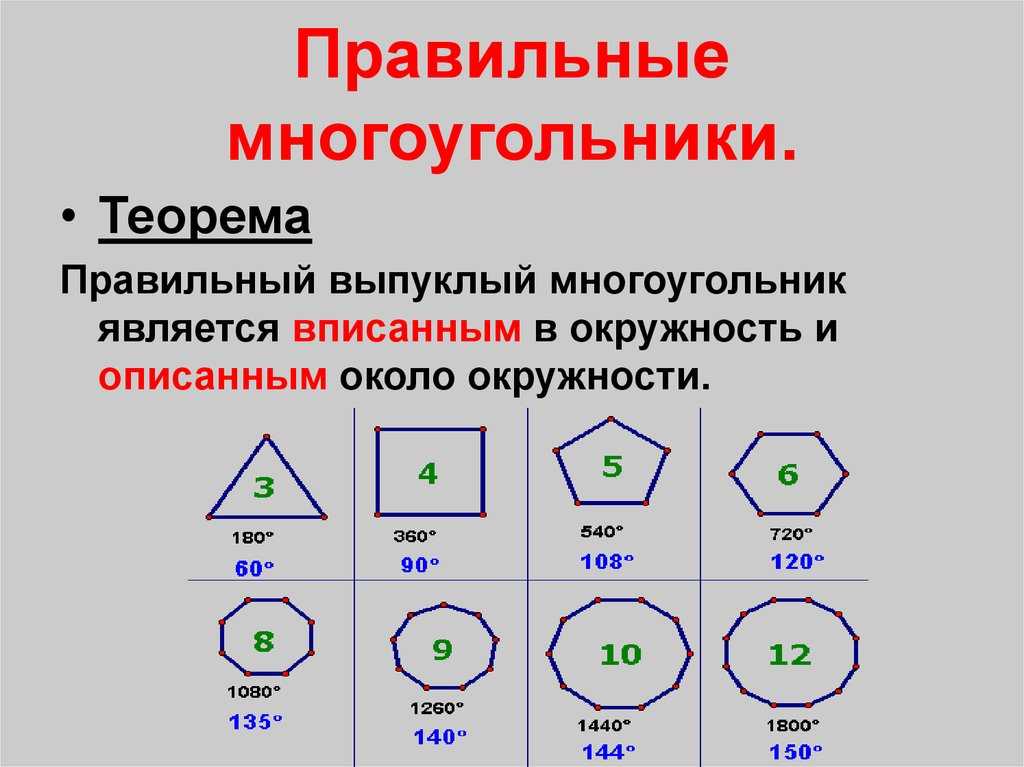
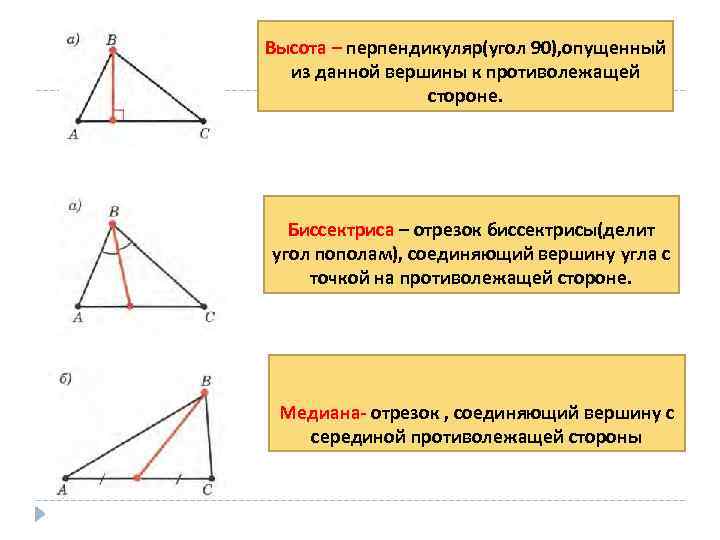
Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

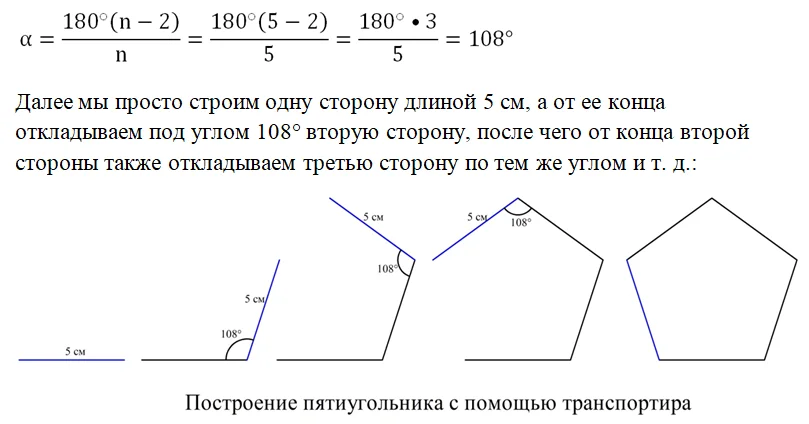
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

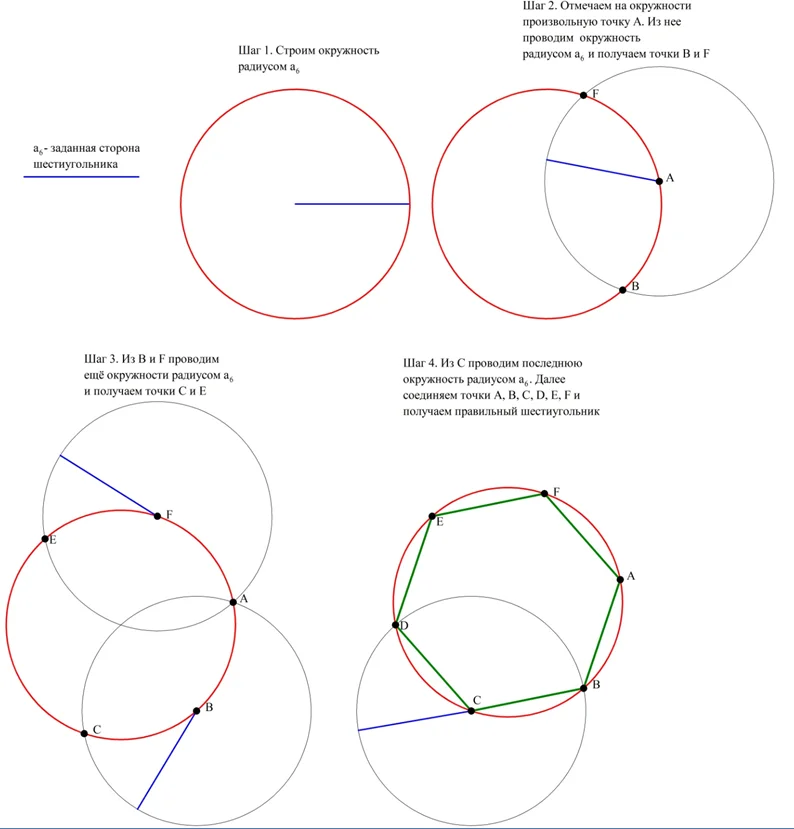
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах

Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности

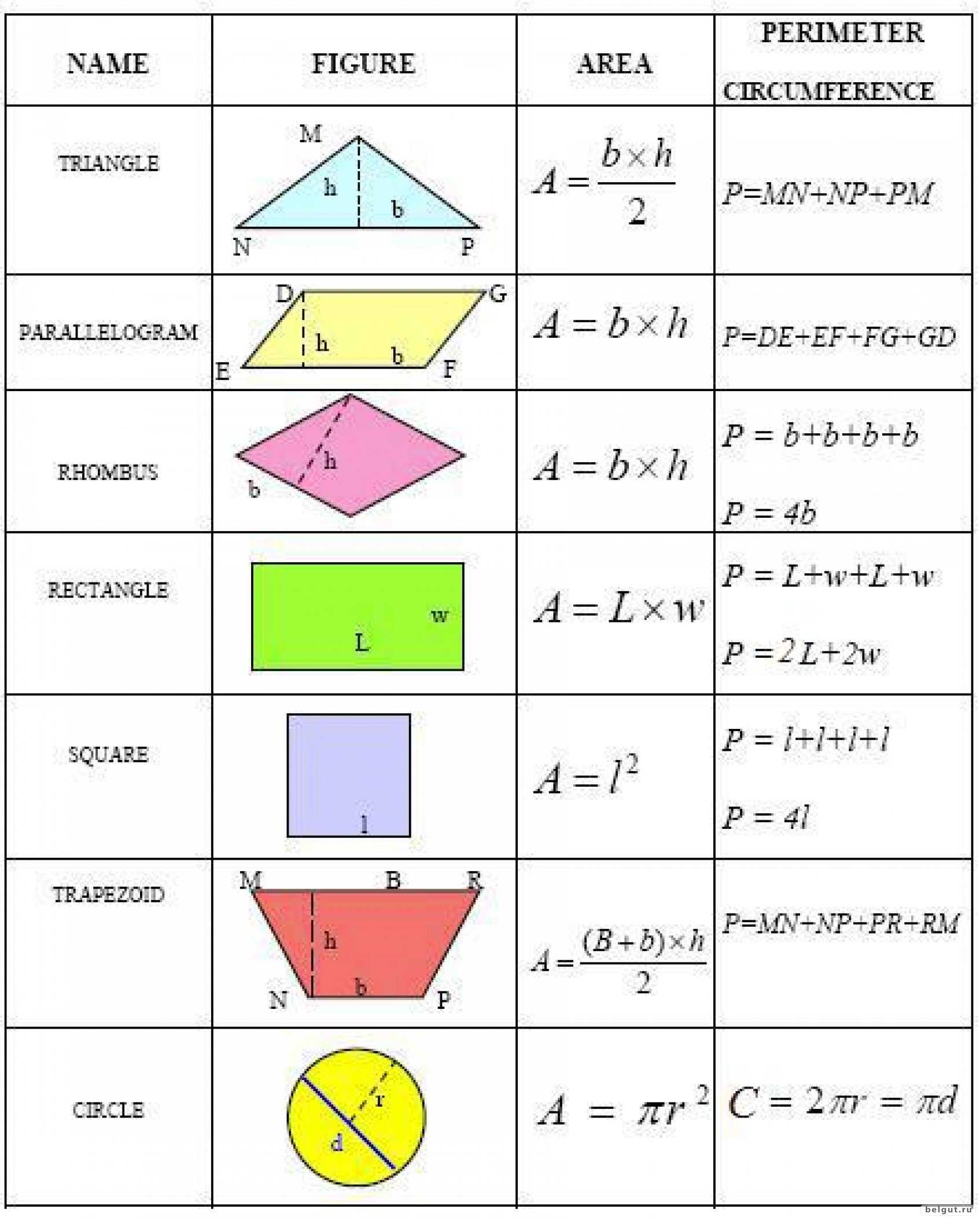
Виды фигур

Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

1. Равносторонние — у которых длина всех отрезков одинаковая.
2. Равнобедренные — треугольники, у которых равны два отрезка из трех.
3. Разносторонние — если длина всех отрезков разная.

Кроме того, принято различать следующие треугольники:

1. Остроугольные.
2. Прямоугольные.
3. Тупоугольные.

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

1. Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
2. Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
3. Четырехугольник, все стороны которого равны, называется ромбом.

На одной прямой не может находиться сразу три вершины четырехугольника.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

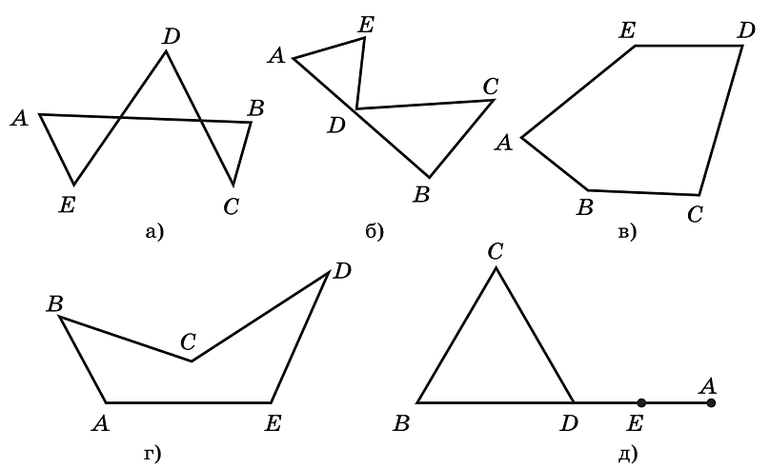
Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

• вершин;
• сторон;
• углов.

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

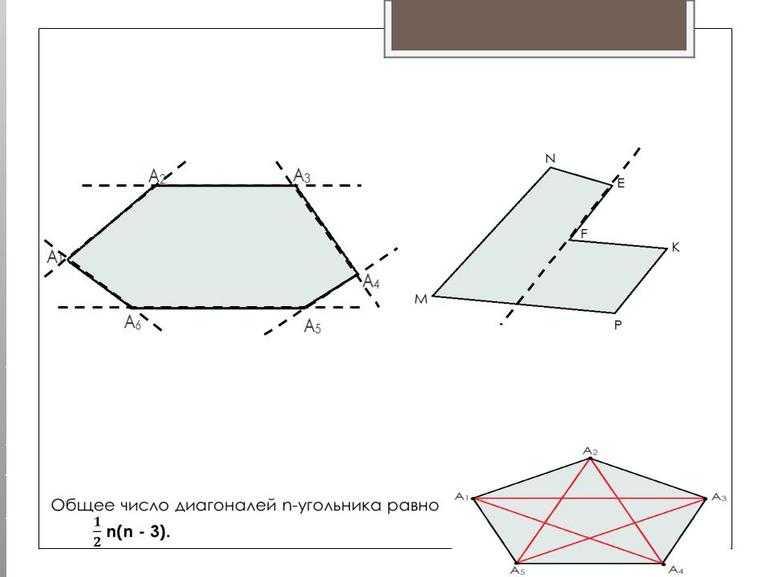
Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n-угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

В природе

Дорога гигантов в Северной Ирландии

Многоугольники появляются в горных породах, чаще всего в виде плоских граней кристаллов , где углы между сторонами зависят от типа минерала, из которого сделан кристалл.

Правильные шестиугольники могут возникать, когда при охлаждении лавы образуются области плотно упакованных столбов базальта , которые можно увидеть на Мосту гигантов в Северной Ирландии или на Дьявольской столбе в Калифорнии .

В биологии поверхность восковых сот, созданных пчелами, представляет собой массив шестиугольников , а стороны и основание каждой соты также представляют собой многоугольники.

Определение

Вершина угла

Вершина угла — это точка, окуда берут начало два луча.

Вершина угла — это точка, откуда берут начало два луча ; где сходятся два отрезка; где две прямые пересекаются; где любая комбинация лучей, отрезков и прямых, образующих две (прямолинейные) «стороны», которые сходятся в одной точке .

Вершина многоугольника многогранника

В многоугольнике вершина называется «выпуклой », если внутренний угол многоугольника меньше π радиан (180° — два прямых угла).
В противном случае вершина называется «вогнутой».

Более обще, вершина многогранника является выпуклой, если пересечение многогранника с достаточно малой сферой , имеющей вершину в качестве центра, представляет собой выпуклую фигуру; в противном же случае вершина является вогнутой.

Вершины многогранника связаны с вершинами графа , поскольку многогранника является графом, вершины которого соответствуют вершинам многогранника , а следовательно, граф многогранника можно рассматривать как одномерный симплициальный комплекс , вершинами которого служат вершины графа. Однако, в теории графов вершины могут иметь менее двух инцидентных рёбер , что обычно не разрешается для вершин геометрических. Также имеется связь между геометрическими вершинами и вершинами кривой , точками экстремумов её кривизны — вершины многоугольника в некотором смысле являются точками бесконечной кривизны, и, если многоугольник приблизить гладкой кривой, точки экстремальной кривизны будут лежать вблизи вершин многоугольника . Однако, приближение многоугольника с помощью гладкой кривой даёт дополнительные вершины в точках минимальной кривизны.

«Рты»

Основная вершина
x
i
{\displaystyle x_{i}}

простого многоугольника
P
{\displaystyle P}

называется «ртом», если диагональ

{\displaystyle }
лежит вне
P
{\displaystyle P}

.

Вершины в компьютерной графике

В компьютерной графике объекты часто представляются как триангулированные многогранники , в которых вершинам объекта сопоставляются не только три пространственные координаты , но и другая необходимая для правильного построения изображения объекта графическая информация, такая как цвет, отражательная способность , текстура , нормали вершин . Эти свойства используются при построении изображения с помощью

В Викисловаре есть статья «вершина» Вершина верхняя точка чего либо. Термин вершина может также означать: В топографии … Википедия

ВЕРШИНА
— (1) В. конуса точка пересечения образующих конуса; (2) В. многогранника точка, в кото рой сходятся соседние рёбра многогранника; (3) В. многоугольника точка, в которой сходятся две соседние стороны многоугольника; (4) В. параболы точка… … Большая политехническая энциклопедия

ВЕРШИНА, в математике точка, в которой сходятся две стороны треугольника или другого многоугольника, либо пересекаются три и более сторон пирамиды или другого многогранника. Вершиной называют также верхнюю точку конуса … Научно-технический энциклопедический словарь

Построение выпуклой оболочки методом «разделяй и властвуй» алгоритм построения выпуклой оболочки. Содержание 1 Описание 2 Определения 3 Реализация … Википедия

Построение выпуклой оболочки методом «разделяй и властвуй» алгоритм построения выпуклой оболочки. Содержание 1 Описание 2 Определения 3 Реализация 4 Сложность алгоритма … Википедия

Проверка принадлежности данной точки данному многоугольнику На плоскости даны многоугольник и точка. Многоугольник может быть как выпуклым, так и невыпуклым. Требуется решить вопрос о принадлежности точки многоугольнику. Благодаря тому, что… … Википедия

Часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера

Дискретная группа голоморфных преобразований (открытого) круга Кна сфере Римана, т. е. круга или полуплоскости на комплексной плоскости. Чаще всего в качестве Кберут верхнюю полуплоскость или единичный круг В первом случае элементы Ф. г. являются … Математическая энциклопедия

Существуют разные точки зрения на то, что считать многоугольником. В школьном курсе геометрии используют одно из следующих определений.

Определение 1

Многоугольник

— это фигура, составленная из отрезков

так, что смежные отрезки
(то есть соседние отрезки с общей вершиной, например, A1A2 и A2A3) не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

Определение 2

Многоугольником называется простая замкнутая .

Точки

называются вершинами многоугольника
, отрезки

— сторонами многоугольника
.

Сумма длин всех сторон называется периметром многоугольника
.

Многоугольник, который имеет n вершин (а значит, и n сторон) называется n — угольником
.

Многоугольник, который лежит в одной плоскости, называется плоским
. Когда говорят о многоугольнике, если не сказано иначе, подразумевается, что речь идёт о плоском многоугольнике.

Две вершины, принадлежащие одной стороне многоугольника, называются соседними
. Например, A1 и A2, A5 и A6 — соседние вершины.

Отрезок, который соединяет две несоседние вершины, называется диагональю многоугольника
.

Выясним, сколько диагоналей имеет многоугольник.

Из каждой из n вершин многоугольника исходит n-3 диагонали

(всего вершин n. Не считаем саму вершину и две соседние, которые не образуют с данной вершиной диагонали. Для вершины A1, например, не учитываем саму A1 и соседние вершины A2 и A3).

Таким образом, каждой из n вершин соответствует n-3 диагонали. Поскольку одна диагональ относится сразу к двум вершинам, чтобы найти количество диагоналей многоугольника, надо произведение n(n-3) разделить пополам.

Следовательно, n — угольник имеет

диагонали.

Любой многоугольник делит плоскость на две части — внутреннюю и внешнюю области многоугольника. Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником.

Добавление многоугольника на карту

Пусть и — ближайшее левое и правое ребро относительно split вершины, которые пересекает в данный момент. Тип вершины, хранящийся в не имеет значения. Таким образом, чтобы построить диагональ для split вершины нужно обратиться к указателю её левого ребра, которое пересекает в данный момент.

В подходе, описанном выше, требуется находить пересечения заметающей прямой и левых ребёр многоугольника. Создадим приоритетную очередь из вершин, в которой приоритетом будет -координата вершины. Если две вершины имеют одинаковые -координаты, больший приоритет у левой. Вершины будут добавляться на «остановках» заметающей прямой.

Отсюда не пересекает ни одну из сторон в посторонних точках. Поскольку внутри никаких вершин вершин находиться не может, и оба конца любой добавленной ранее диагонали должны лежать выше, диагональ не может пересекать никакую из ранее добавленных диагоналей.

Будем проходить сверху вниз по вершинам многоугольника проводя диагонали где это возможно. Следовательно, наш многоугольник лежит в полосе с границами b и c, откуда получаем, что P – наиболее удаленная от прямой b, содержащей сторону a , вершина многоугольника.

1. Понятие «многоугольник»

В курсе гео­мет­рии мы изу­ча­ем свой­ства гео­мет­ри­че­ских фигур и уже рас­смот­ре­ли про­стей­шие из них: тре­уголь­ни­ки и окруж­но­сти. При этом мы об­суж­да­ли и кон­крет­ные част­ные слу­чаи этих фигур, такие как пря­мо­уголь­ные, рав­но­бед­рен­ные и пра­виль­ные тре­уголь­ни­ки. Те­перь при­шло время по­го­во­рить о более общих и слож­ных фи­гу­рах – мно­го­уголь­ни­ках.

С част­ным слу­ча­ем мно­го­уголь­ни­ков мы уже зна­ко­мы – это тре­уголь­ник (см. Рис. 1).

Рис. 1. Тре­уголь­ник

В самом на­зва­нии уже под­чер­ки­ва­ет­ся, что это фи­гу­ра, у ко­то­рой три угла. Сле­до­ва­тель­но, в мно­го­уголь­ни­ке их может быть много, т.е. боль­ше, чем три. На­при­мер, изоб­ра­зим пя­ти­уголь­ник (см. Рис. 2), т.е. фи­гу­ру с пятью уг­ла­ми.

Рис. 2. Пя­ти­уголь­ник. Вы­пук­лый мно­го­уголь­ник

Опре­де­ле­ние.Мно­го­уголь­ник – фи­гу­ра, со­сто­я­щая из несколь­ких точек (боль­ше двух) и со­от­вет­ству­ю­ще­го ко­ли­че­ства от­рез­ков, ко­то­рые их по­сле­до­ва­тель­но со­еди­ня­ют. Эти точки на­зы­ва­ют­ся вер­ши­на­ми мно­го­уголь­ни­ка, а от­рез­ки – сто­ро­на­ми. При этом ни­ка­кие две смеж­ные сто­ро­ны не лежат на одной пря­мой и ни­ка­кие две несмеж­ные сто­ро­ны не пе­ре­се­ка­ют­ся.

Опре­де­ле­ние.Пра­виль­ный мно­го­уголь­ник – это вы­пук­лый мно­го­уголь­ник, у ко­то­ро­го все сто­ро­ны и углы равны.

Любой мно­го­уголь­ник раз­де­ля­ет плос­кость на две об­ла­сти: внут­рен­нюю и внеш­нюю. Внут­рен­нюю об­ласть также от­но­сят кмно­го­уголь­ни­ку.

Иными сло­ва­ми, на­при­мер, когда го­во­рят о пя­ти­уголь­ни­ке , имеют в виду и всю его внут­рен­нюю об­ласть, и гра­ни­цу. А ко внут­рен­ней об­ла­сти от­но­сят­ся и все точки, ко­то­рые лежат внут­ри мно­го­уголь­ни­ка, т.е. точка  тоже от­но­сит­ся к пя­ти­уголь­ни­ку (см. Рис. 2).

Мно­го­уголь­ни­ки еще ино­гда на­зы­ва­ют n-уголь­ни­ка­ми, чтобы под­черк­нуть, что рас­смат­ри­ва­ет­ся общий слу­чай на­ли­чия ка­ко­го-то неиз­вест­но­го ко­ли­че­ства углов (n штук).

Опре­де­ле­ние. Пе­ри­метр мно­го­уголь­ни­ка – сумма длин сто­рон мно­го­уголь­ни­ка.

Те­перь надо по­зна­ко­мить­ся с ви­да­ми мно­го­уголь­ни­ков. Они де­лят­ся на вы­пук­лые и невы­пук­лые. На­при­мер, мно­го­уголь­ник, изоб­ра­жен­ный на Рис. 2, яв­ля­ет­ся вы­пук­лым, а на Рис. 3 невы­пук­лым.

Рис. 3. Невы­пук­лый мно­го­уголь­ник

Правильные многоугольники

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

И ответ: можно!

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

Сумма всех его углов равна \( \displaystyle 180{}^\circ \left( 8-2 \right)=1080{}^\circ \). 

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:

\( \displaystyle \angle A=\frac{1080{}^\circ }{8}=135{}^\circ \).

Что мы еще должны знать?

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

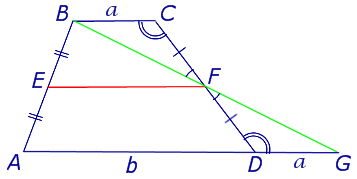
Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)

Значит, \( \displaystyle \frac{r}{R}=\sin \angle x\) – и это не только в восьмиугольнике!

Чему же равен в нашем случае \( \displaystyle \angle x\)?

Ровно половине \( \displaystyle \angle G\), представь себе!

Значит \( \displaystyle \angle x=\frac{135{}^\circ }{2}=67,5{}^\circ \).

Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac{r}{R}=\sin 67,5{}^\circ \).

Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?

И тот же ответ: конечно можно!

Презентация на тему: » Многоугольники Многоугольником называется … вершинами многоугольника.Вершины ломаной называются … сторонами многоугольника.Стороны ломаной называются …» — Транскрипт:

1

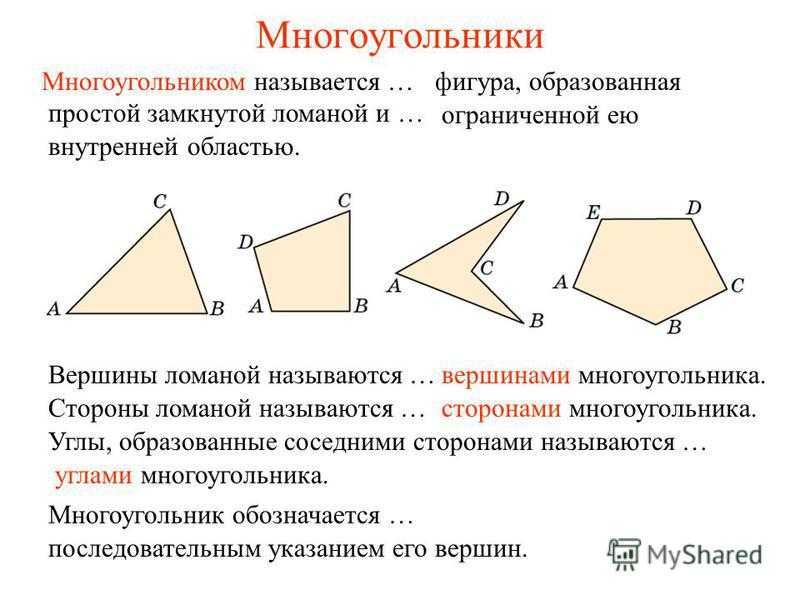
Многоугольники Многоугольником называется … вершинами многоугольника.Вершины ломаной называются … сторонами многоугольника.Стороны ломаной называются … углами многоугольника. Углы, образованные соседними сторонами называются … ограниченной ею внутренней областью. последовательным указанием его вершин. Многоугольник обозначается … фигура, образованная простой замкнутой ломаной и …

2

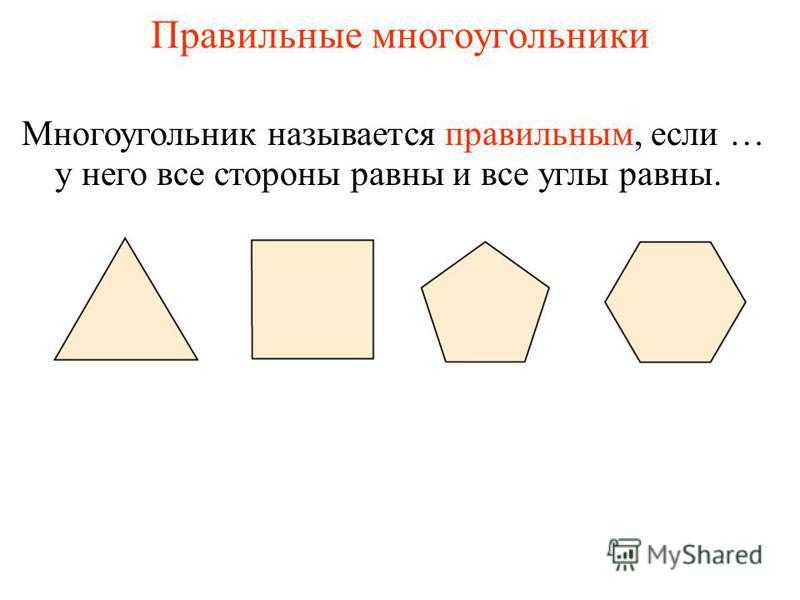
Правильные многоугольники у него все стороны равны и все углы равны. Многоугольник называется правильным, если …

3

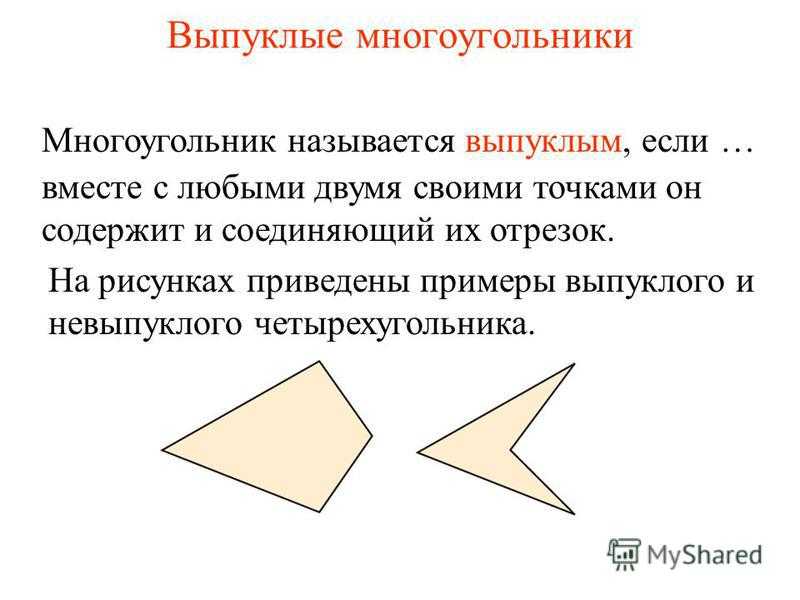
Выпуклые многоугольники вместе с любыми двумя своими точками он содержит и соединяющий их отрезок. Многоугольник называется выпуклым, если … На рисунках приведены примеры выпуклого и невыпуклого четырехугольника.

4

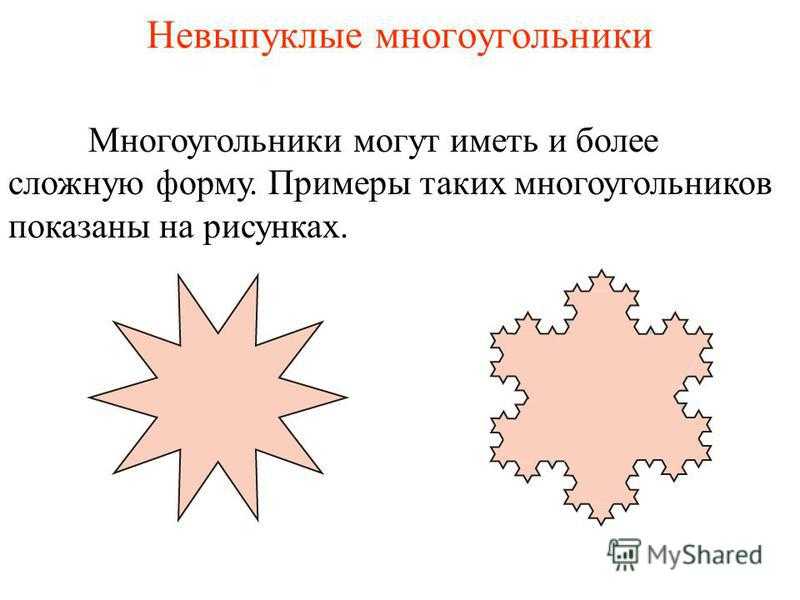
Невыпуклые многоугольники Многоугольники могут иметь и более сложную форму. Примеры таких многоугольников показаны на рисунках.

5

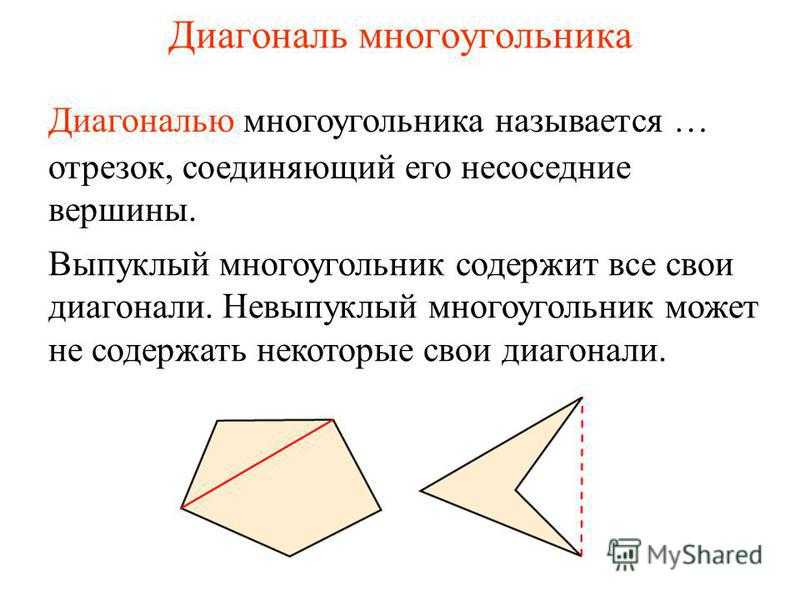
Диагональ многоугольника отрезок, соединяющий его не соседние вершины. Диагональю многоугольника называется … Выпуклый многоугольник содержит все свои диагонали. Невыпуклый многоугольник может не содержать некоторые свои диагонали.

6

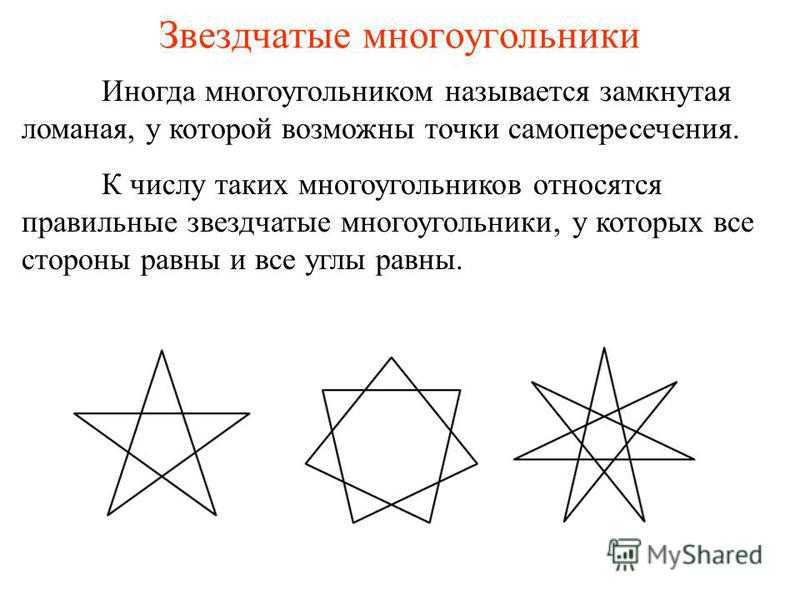
Звездчатые многоугольники Иногда многоугольником называется замкнутая ломаная, у которой возможны точки самопересечения. К числу таких многоугольников относятся правильные звездчатые многоугольники, у которых все стороны равны и все углы равны.

7

Вопрос 1 Какая фигура называется многоугольником? Что называется: вершинами; сторонами; углами многоугольника? Ответ: Фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью, называется многоугольником. Вершины ломаной называются вершинами многоугольника, стороны ломаной — сторонами многоугольника, а углы, образованные соседними сторонами, — углами многоугольника.

8

Вопрос 2 Какой многоугольник называется n- угольником? Ответ: n – угольником называется многоугольник, у которого n углов.

9

Вопрос 3 Какой многоугольник называется правильным? Ответ: Многоугольник называется правильным, если у него все стороны равны и все углы равны.

10

Вопрос 4 Какой многоугольник называется выпуклым? Ответ: Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок.

11

Вопрос 5 Что называется диагональю многоугольника? Ответ: Диагональю многоугольника называется отрезок, соединяющий его не соседние вершины.

12

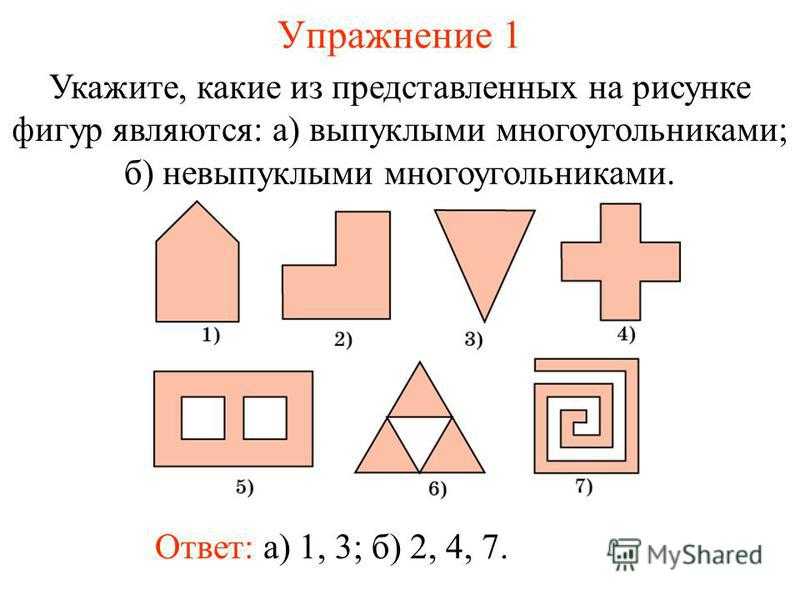
Упражнение 1 Укажите, какие из представленных на рисунке фигур являются: а) выпуклыми многоугольниками; б) невыпуклыми многоугольниками. Ответ: а) 1, 3; б) 2, 4, 7.

13

Упражнение 2 Какая имеется зависимость между числом вершин, числом углов и числом сторон многоугольника? Ответ: Число вершин равно числу углов и равно числу сторон.

14

Упражнение 3 Нарисуйте шестиугольник, изображенный на рисунке. Является ли он правильным? Ответ: Нет.

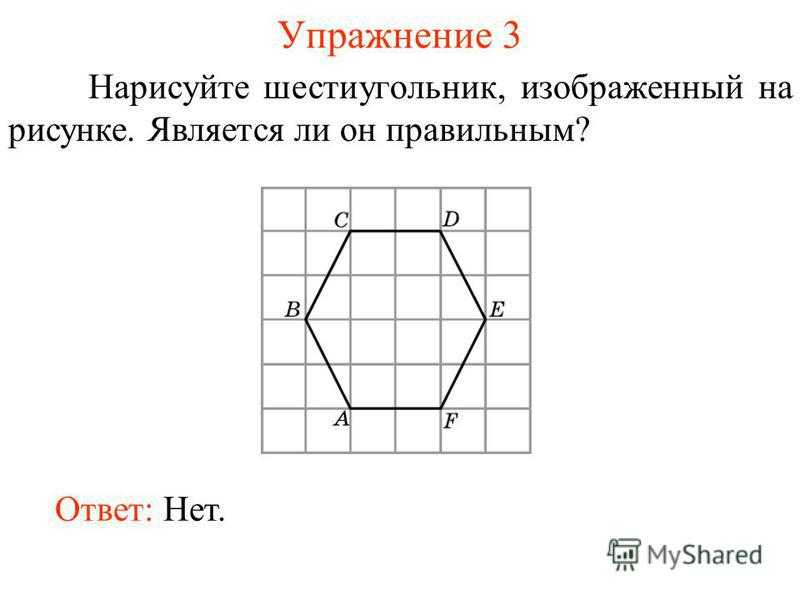
15

Упражнение 4 Нарисуйте восьмиугольник, изображенный на рисунке. Является ли он правильным? Ответ: Нет.

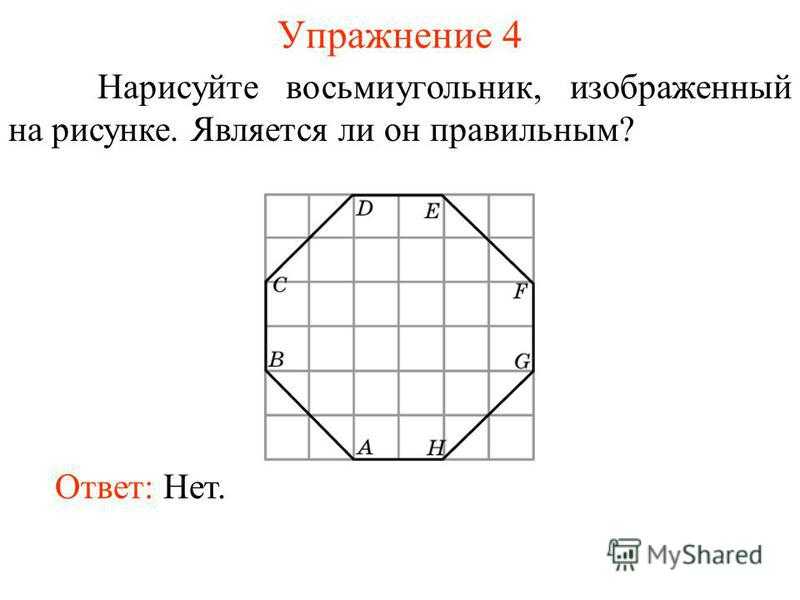
16

Упражнение 5 На клетчатой бумаге изобразите какой- нибудь четырёхугольник, вершинами которого являются точки A, B, C и D. Сколько таких четырехугольников? Ответ: 3.

17

Упражнение 6 Сколько диагоналей имеет: а) треугольник?0; б) четырехугольник? 2; в) пятиугольник? 5; г) шестиугольник? 9; д) n-угольник?

18

Упражнение 7 Может ли многоугольник иметь ровно: а) 10 диагоналей?нет; б) 20 диагоналей?да; в)* 30 диагоналей?нет.

19

Упражнение 8 Существует ли многоугольник, число диагоналей которого равно числу его сторон? Ответ: Да, пятиугольник.

20

Упражнение 9 Выпуклый многоугольник имеет 35 диагоналей. Сколько у него сторон? Ответ: 10.

21

Упражнение 10 На сколько треугольников делится выпуклый: а) 4-угольник; б) 5-угольник; в) 6-угольник; г)* n-угольник своими диагоналями, проведенными из одной вершины? Ответ: а) 2;б) 3;в) 4;г) n-2.

22

Упражнение 11 Приведите пример, когда общей частью (пересечением) двух треугольников является: а) треугольник; б) четырехугольник; в) пятиугольник; г) шестиугольник. Ответ:

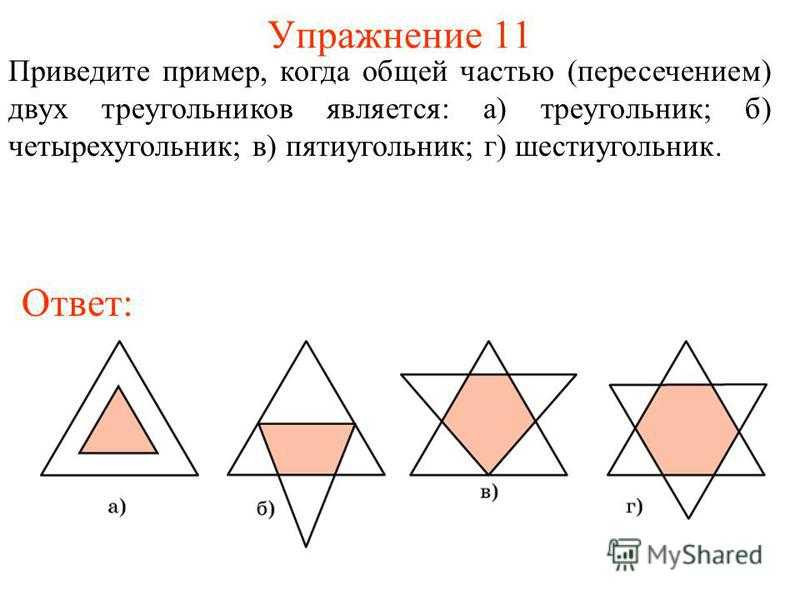
23

Упражнение 12 Может ли пересечением двух треугольников быть семиугольник? Ответ: Нет.

24

Упражнение 13* Приведите пример, когда общей частью (пересечением) треугольника и четырехугольника является восьмиугольник. Ответ:

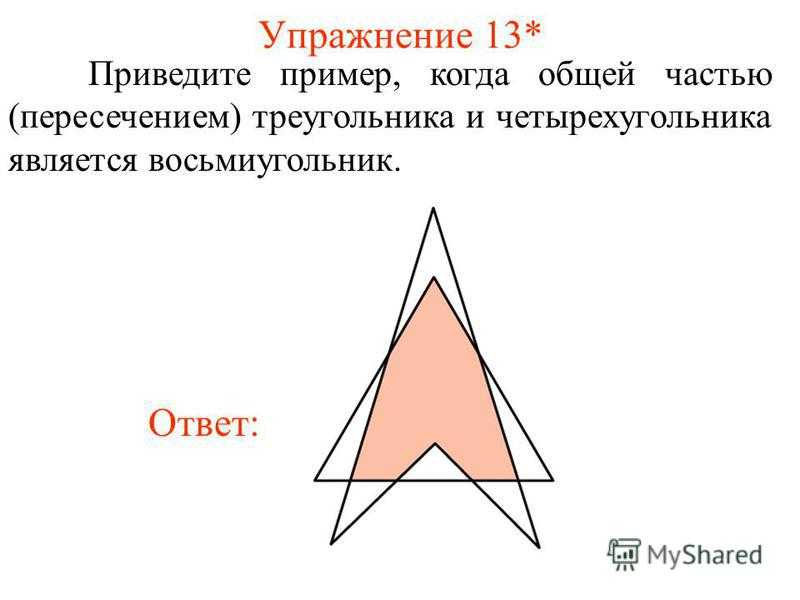
25

Упражнение 14* На рисунке изображен многоугольник ABCDE. Из точки O видны полностью стороны AB, DE и AE и лишь частично сторона CD. Нарисуйте какой-нибудь многоугольник и точку O внутри него так, чтобы ни одна из сторон не была видна из нее полностью. Ответ:

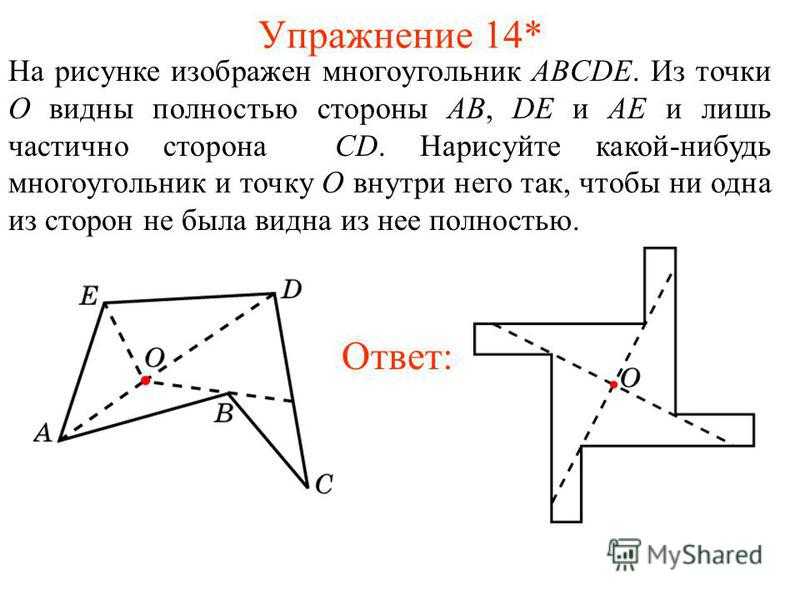
26

Упражнение 15 Сколько сторон имеют звездчатые многоугольники, изображенные на рисунке? Ответ: 5; 7; 7.

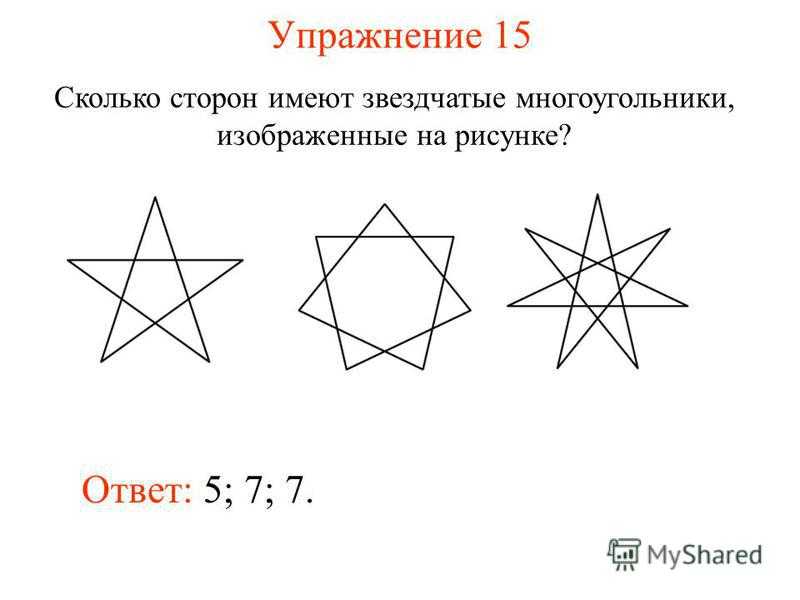
27

Упражнение 16 На сколько частей разбивают плоскость правильные звездчатые многоугольники, изображенные на рисунке? Ответ: 7; 9; 16.

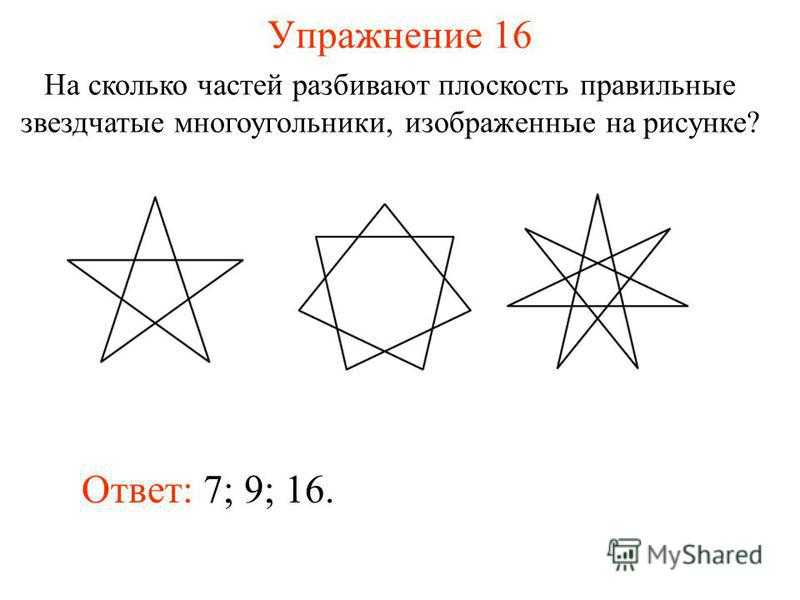
Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

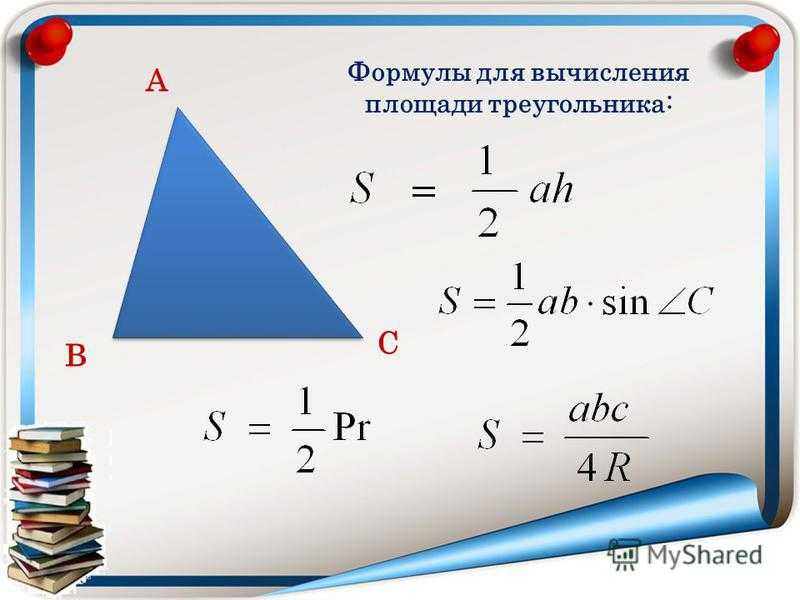
Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Диагонали n — угольника

Фигура	Рисунок	Описание
Диагональмногоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагоналиn – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершиныn – угольника, делят n – угольник наn – 2 треугольника
Все диагоналиn – угольника		Число диагоналей n – угольника равно

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Задание стиля многоугольника

У любого простого -вершинного многоугольника всегда существует триангуляция, причём количество треугольников в ней независимо от самой триангуляции. В общем случае в произвольном -угольнике всего возможных вариантов построения диагоналей. Для некоторых классов многоугольников предыдущую оценку можно улучшить. Например, если многоугольник выпуклый, то достаточно лишь выбирать одну его вершину и соединять со всеми остальными, кроме его соседей.

Тогда докажем, что содержит split и merge вершины. Чтобы сделать многоугольник монотонным, нужно избавиться от split и merge вершин путём проведения непересекающихся дигоналей из таких вершин. Рассмотрим горизонтальную заметающую прямую, будем перемещать её сверху вниз вдоль плоскости на которой лежит исходный многоугольник. Будем останавливать её в каждой вершине многоугольника.

Именование

Слово многоугольник происходит от позднего латинского polygōnum (существительное), от греческого πολύγωνον ( polygōnon / polugōnon ), существительного, использующего средний язык от πολύγωνος ( polygōnos / polugōnos , прилагательное мужского рода), что означает «многоугольный». Отдельные многоугольники называются (а иногда классифицируют) в соответствии с числом сторон, сочетая греческий -derived числового префикса с суффиксом -угольник , например , пятиугольник , двенадцатиугольником . Треугольник , четырехугольник и девятиугольник исключение.

Помимо десятиугольников (10-сторонних) и додекагонов (12-сторонних) математики обычно используют числовые обозначения, например 17-угольник и 257-угольник.

Исключения существуют для побочных подсчетов, которые легче выразить в устной форме (например, 20 и 30) или которые используются не математиками. Некоторые специальные многоугольники также имеют свои собственные имена; например, правильный пятиугольник звезды также известен как пентаграмма .

Имена многоугольников и прочие свойства

Имя	Стороны	Характеристики
моногон	1	Обычно не считается многоугольником, хотя в некоторых дисциплинах, таких как теория графов, иногда используется этот термин.
Digon	2	Обычно не считается многоугольником на евклидовой плоскости, хотя может существовать как сферический многоугольник .
треугольник (или тригон)	3	Простейший многоугольник, который может существовать в евклидовой плоскости. Можно выложить самолет плиткой .
четырехугольник (или четырехугольник)	4	Простейший многоугольник, который может пересекаться; простейший многоугольник, который может быть вогнутым; простейший многоугольник, который может быть нециклическим. Можно выложить самолет плиткой .
пятиугольник	5	Простейший многоугольник, который может существовать как правильная звезда. Звездный пятиугольник известен как пентаграмма или пентакль.
шестиугольник	6	Можно выложить самолет плиткой .
семиугольник (или септагон)	7	Простейший многоугольник такой, что правильную форму невозможно построить с помощью циркуля и линейки . Однако его можно построить, используя конструкцию Нойсиса .
восьмиугольник	8
нонагон (или эннеагон)	9	«Нонагон» смешивает латинский [ novem = 9] с греческим; «эннеагон» — чисто греческое.
десятиугольник	10
hendecagon (или undecagon)	11	Простейший многоугольник такой, что правильную форму нельзя построить с помощью циркуля, линейки и трисектора угла .
двенадцатиугольник (или двенадцатиугольник)	12
трехугольник (или трехугольник)	13
тетрадекагон (или тетракаидакагон)	14
пятиугольник (или пятиугольник)	15
hexadecagon (или hexakaidecagon)	16
гептадекагон (или гептадекагон)	17	Конструируемый многоугольник
octadecagon (или octakaidecagon)	18
enneadecagon (или enneakaidecagon)	19
икосагон	20
икоситетракон (или икосикаитетракон)	24
триаконтагон	30
тетраконтагон (или тессараконтагон)	40
пятиугольник (или пятиконтагон)	50
шестиугольник (или шестиугольник)	60
гептаконтагон (или hebdomecontagon)	70
восьмиугольник (или огдоэконтагон)	80
эннеконтагон (или эннеконтагон)	90
гектогон (или гекатонтагон)	100
257-угольник	257	Конструируемый многоугольник
чилигон	1000	Философы, включая Рене Декарта , Иммануила Канта , Дэвида Юма , использовали хилиагон в качестве примера в своих дискуссиях.
мириагон	10 000	Используется в качестве примера в некоторых философских дискуссиях, например, в « Размышлениях о первой философии» Декарта.
65537-угольник	65 537	Конструируемый многоугольник
мегагон	1 000 000	Как и в случае с примером хилиагона Рене Декарта, многоугольник с миллионами сторон использовался как иллюстрация четко определенной концепции, которую невозможно визуализировать. Мегагон также используется как иллюстрация схождения правильных многоугольников в круг.
апейрогон	∞	Вырожденный многоугольник с бесконечным числом сторон.

Создание высших имен

Чтобы создать имя многоугольника с более чем 20 и менее чем 100 ребрами, объедините префиксы следующим образом. Термин «кай» применяется к 13-угольникам и выше, использовался Кеплером и поддерживался Джоном Х. Конвеем для ясности конкатенированных префиксных чисел при именовании квазирегулярных многогранников .

Десятки	и	Единицы	последний суффикс
-kai-	1	-hena-	-угольник
20	icosi- (icosa- в одиночестве)	2	-ди-
30	триаконта- (или триконта-)	3	-три-
40	тетраконта- (или тессаракта-)	4	-тетра-
50	пентаконта- (или пентеконта-)	5	-penta-
60	гексаконта- (или гексеконта-)	6	-hexa-
70	гептаконта- (или гебдомеконта-)	7	-гепта-
80	октаконта- (или огдоэконта-)	8	-окта-
90	эннеаконта- (или эненеконта-)	9	-ennea-