Треугольник. медиана, биссектриса, высота, средняя линия

См. также

Шаблон:Викисловарь
Шаблон:Кол

• Барицентр
• Барицентрические координаты
• Высота треугольника
• Вписанная окружность
• Вписанная и вневписанные в треугольник окружности
• Замечательные точки треугольника
• Инцентр
• Окружность
• Окружность девяти точек
• Ортоцентр
• Правильный треугольник
• Признаки подобия треугольников
• Прямая Симсона
• Прямая Эйлера
• Прямоугольный треугольник
• Равносторонний треугольник
• Равнобедренный треугольник
• Средняя линия треугольника
• Сферический треугольник
• Теорема косинусов
• Теорема о сумме углов треугольника
• Теорема о трезубце
• Теорема синусов
• Теорема Харкорта
• Точки Аполлония
• Точка Жергона
• Точка Лемуана
• Точка Нагеля
• Точки Наполеона
• Точка Парри
• Точка Понселе
• Точки Торричелли
• Точка Ферма
• Треугольник Рёло
• Трилинейные координаты
• Формула Герона
• Центр девяти точек
• Центр тяжести
• Центр Шпикера
• Центроид
• Центроид треугольника

Эллипс Штейнера

Шаблон:Конец кол

Взаимное отношение углов и сторон в треугольнике

Теорема 25. В равнобедренном треугольнике против равных сторон лежат равные углы.

Дан равнобедренный треугольник ABC (черт. 49), т. е. треугольник, у которого AB = BC.

Требуется доказать, что ∠A = ∠C.

Доказательство. Соединим точку B с точкой D, которая является серединой стороны AC.

Два треугольника ABD и BDC равны, ибо имеют по три равных стороны. Действительно:

BD — общая сторона;
AD = DC по построению (D середина отрезка AC);
AB = BC по условию.

В равных треугольниках против равных сторон лежат равные углы, следовательно,

∠A = ∠C (ЧТД).

Теорема 26 (обратная 25). В треугольнике против равных углов лежат равные стороны.

Дано. В треугольнике ABC ∠A = ∠C (черт. 50).

Требуется доказать, что AB = BC.

Доказательство. Положим, сторона AB > BC. Тогда, отложив на стороне AB часть AD равную BC, имеем два треугольника ADC и ABC, у которых

AC — общая сторона,
AD = BC по построению, ∠A = ∠C по условию.

Таким образом, AC и AD, две стороны треугольника ADC и уголь между ними A соответственно равны AC и BC, двум сторонам треугольника ABC, и углу C между ними. При этих условиях треугольники ADС и ABC были бы равны, что очевидно несообразно, ибо ∆ADC < ∆ABC, как часть меньше целого, следовательно, AB не может быть больше BC. Точно также можно доказать, что сторона AB не может быть меньше стороны BC, следовательно, AB = BC (ЧТД).

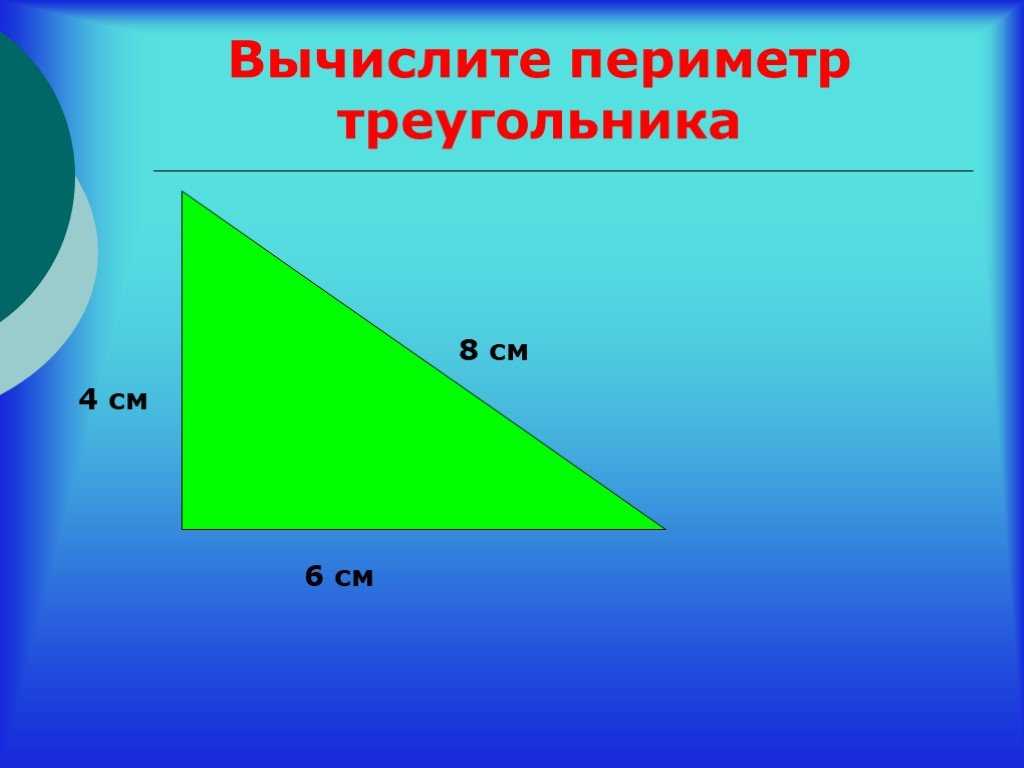
Теорема 27. В треугольнике против большего угла лежит большая сторона.

Дано. В треугольнике ABC (черт. 51) ∠A >∠C.

Требуется доказать, что BC > AB.

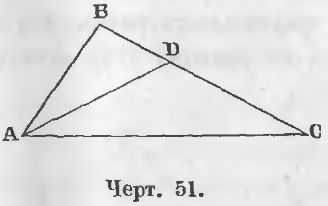
Доказательство. Построим при точке A угол DAC равный углу C, тогда в треугольнике BDA

AD + DB > AB.

В равнобедренном треугольнике ADC

AD = DC

следовательно, предыдущее неравенство примет вид

DC + DB > AB

откуда

BC > AB (ЧТД).

Теорема 28 (обратная 27). В треугольнике против большей стороны лежит больший угол.

Дано. В треугольнике ABC (черт. 51) BC > AB.

Требуется доказать, что ∠BAC = ∠BCA.

Доказательство. a) Угол A не может быть равен углу C, ибо тогда сторона AB равнялась бы стороне BC (теорема 26).

b) Угол A не может быть меньше C, ибо тогда сторона BC была бы меньше AB (теорема 27), следовательно, BC > AB (ЧТД).

Свойства прямой

1. Через любые две точки можно провести только одну прямую линию.

Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.

2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.

3. Через одну точку можно провести бесконечно много прямых.

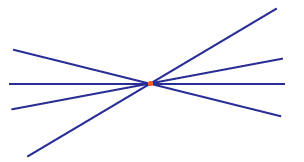
4. Есть точки лежащие на прямой и не лежащие на ней.

Точки N и M лежат на прямой a. Точка L не лежит на прямой a.

Для записи принадлежности точки к прямой используется символ принадлежности – ∈. Например, запись M ∈ a обозначает, что точка M принадлежит прямой a. Для того, чтобы указать что точка не принадлежит прямой можно использовать символ ∉. Например, запись L ∉ a обозначает, что точка L не принадлежит прямой a.

5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.

На рисунке изображена прямая с тремя точками A, B и C, лежащими на ней. Про эти точки можно сказать: Точка B лежит между точками A и C, точка B разделяет точки A и C, – или, – точки A и C лежат по разные стороны от точки B. Также можно сказать: Точки B и C лежат по одну сторону от точки A, они не разделяются точкой A, – или, – точки A и B лежат по одну сторону от точки C.

6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.

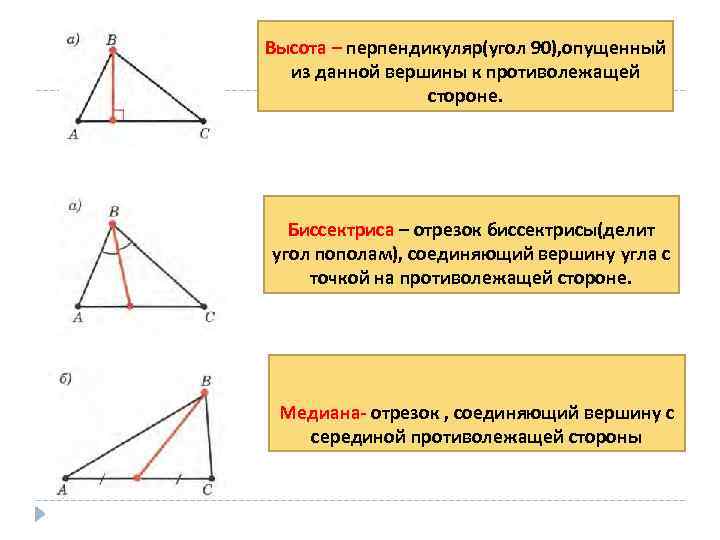
Высота треугольника

Высота треугольника — это отрезок, соединяющий вершину с основанием вершины и образующий прямой угол (перпендикуляр) с основанием или ее продолжением.

На рисунке мы нарисовали разные виды высоты в зависимости от типа треугольника

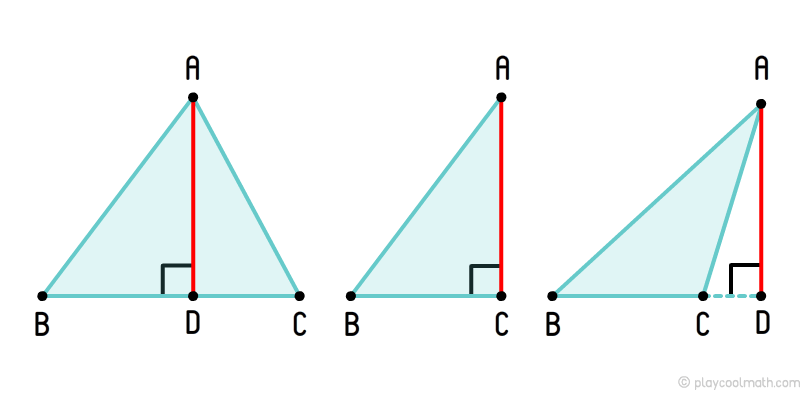
Точка пересечения всех высот называется ортоцентром. У тупоугольного треугольника ортоцентр лежит за пределами треугольника. У прямоугольного треугольника ортоцентр всегда совпадает с вершиной прямого угла. У равностороннего треугольника медианы и высоты совпадают, соответственно и ортоцентр с центроидом тоже совпадают.

Для того чтобы измерить прямой угол, тебе понадобиться линейка в виде треугольника. Обычно такие линейки имеют три угла 90°, 60°, 30°. Чтобы провести перпендикуляр и нарисовать высоту треугольника, сопоставь одну сторону линейки с любой стороной треугольника так, чтобы вторая сторона прямого угла линейки проходила через высоту этого основания. Посмотри на рисунок ниже, как мы ищем высоту с помощью треугольной линейки.

Тупоугольный треугольник

Следствие 2. В тупоугольном треугольнике один угол тупой, а два остальные угла острые.

Доказательство. В тупоугольном треугольнике NBC (черт. 47) угол NCB тупой. Продолжая сторону NC, мы находим внешний острый угол BCD. Так как BCD > N и BCD > B, то оба угла N и B тупоугольного треугольника острые. Отсюда делаем заключениев треугольнике не может быть более одного прямого и более одного тупого угла.

Теорема 23. Если две стороны одного треугольника равны двум сторонам другого, а углы, заключающиеся между этими сторонам не равны, то против большего угла лежит большая сторона.

Дано. В двух треугольниках ABC и DEF (черт. 48)

AC = DF, AB = DE, угол BAC > угла EDF.

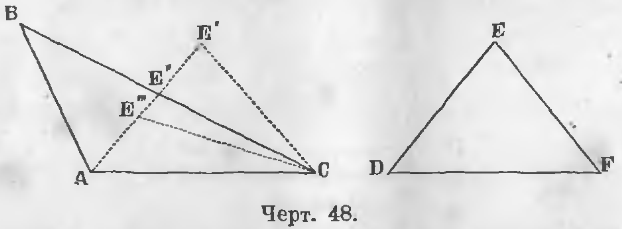
Требуется доказать, что BC > EF.

Доказательство. Наложим треугольник DEF на ABC, стороной DF на AC, точкой D на A. Точка F по равенству сторон DF и AC совпадет с C.

Так как D меньше угла A, то сторона DE пойдет по направлению AE’.

Здесь могут быть три случая: точка E может упасть вне, на сторону и внутри треугольника ABC, т. е. в точках E’, E» и E»’.

1) 1-й случай. Когда точка E упадет в E’, треугольник DEF займет положение треугольника AE’C, следовательно,

AE’ = DE = AB
E’C = EF

Не трудно заметить, что

AE» + E»B > AB
CE» + E»E’ > CE’

Сложив эти неравенства, получим:

AE» + E»B + CE» + E»E’ > AB + CE’

Так как

AE» + E»E = AE’
CE» + E»B = BC

то

AE’ + BC > AB + CE’

Здесь AE’ = AB, следовательно,

BC > CE’ или
BC > EF (ЧТД).

2) 2-й случай. Точка E упадет в E», тогда E»C = EF и

BC > E»C, а следовательно, BC > EF.

3) 3-й случай. Точка E упадет в E»’. В этом случае

AE»’ = DE, E»’C = EF.

По свойству ломаных (теорема 1)

AB + BC > AE»’ + E»’C или
AB + BC > DE + EF.

Так как AB = DE, то последнее неравенство дает

BC > EF

Итак во всех трех случаях BC > EF (ЧТД).

Теорема 24. (Обратная 23). Если две стороны одного треугольника равны двум сторонам другого, а третьи стороны не равны, то против большей стороны лежит больший угол.

Дано. В треугольниках ABC и DEF (черт. 48) AB = DE, AC = DF и BC > EF.

Требуется доказать, что угол BAC > угла EDF.

Доказательство. Здесь могут быть только три предположения: угол BAC может быть равен, меньше или больше угла EDF.

1) Если бы угол BAC равнялся углу EDF, то два треугольника ABC и EDF были бы равны (теорема 20). В этом случае сторона BC равнялась бы стороне EF, что противоречит условию.

2) Если бы угол BAC был меньше угла EDF, то по предыдущей теореме и сторона BC была бы меньше EF, что также противоречит условию; следовательно, угол BAC больше угла EDF (ЧТД).

Признаки равенства треугольников

Файл:Признак 1 равенства треугольников.png

Равенство по двум сторонам и углу между ними

Файл:Признак 2 равенства треугольников.png

Равенство по стороне и двум прилежащим углам

Файл:Признак 3 равенства треугольников.png

Равенство по трем сторонам

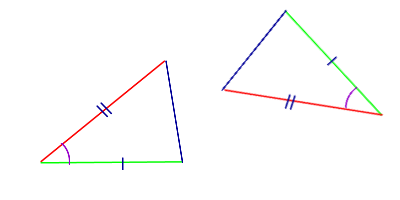
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:

1. a, b, γ (равенство по двум сторонам и углу между ними);
2. a, β, γ (равенство по стороне и двум прилежащим углам);
3. a, b, c (равенство по трём сторонам).

Признаки равенства прямоугольных треугольников:

1. по катету и гипотенузе;
2. по двум катетам;
3. по катету и острому углу;
4. по гипотенузе и острому углу.

В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.

Признаки равенства треугольников

      Треугольники называют равными, если их можно совместить наложением.

      В таблице 3 приведены признаки равенства треугольников.

Таблица 3 – Признаки равенства треугольников

Рисунок	Название признака	Формулировка признака
	Признак равенства треугольников подвум сторонам и углу между ними	Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны
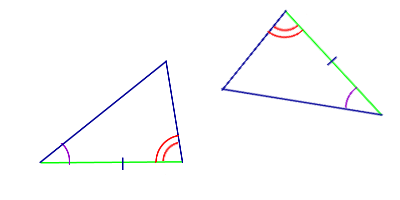	Признак равенства треугольников постороне и двум прилежащим к ней углам	Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
	Признак равенства треугольников потрём сторонам	Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

Признак равенства треугольников по двум сторонам и углу между ними

Формулировка признака.Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны

Признак равенства треугольников по стороне и двум прилежащим к ней углам

Формулировка признака.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

Признак равенства треугольников по трём сторонам

Формулировка признака.Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

Окружность, вписанная в треугольник

Окружность, касающаяся всех трех сторон треугольника, называется вписанной окружностью. Только одна окружность может быть вписана в любой треугольник.

Центром пересечения биссектрис, как мы знаем, является инцентром. Инцентром еще называют центром вписанной окружности. Если от инцентрома до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.

Для того, чтобы вписать окружность в треугольник тебе, понадобится циркуль. Выставь циркуль в инцентром и установи радиус равный расстоянию до любого основанию по перпендикуляру. Круговым движением нарисуй окружность.

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

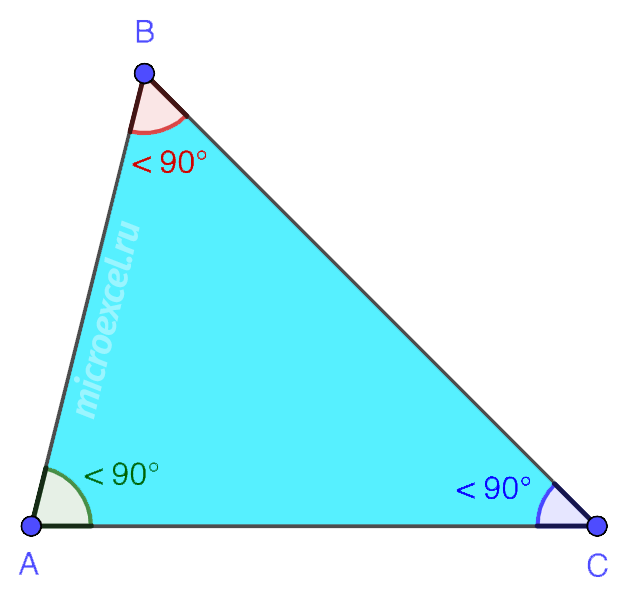
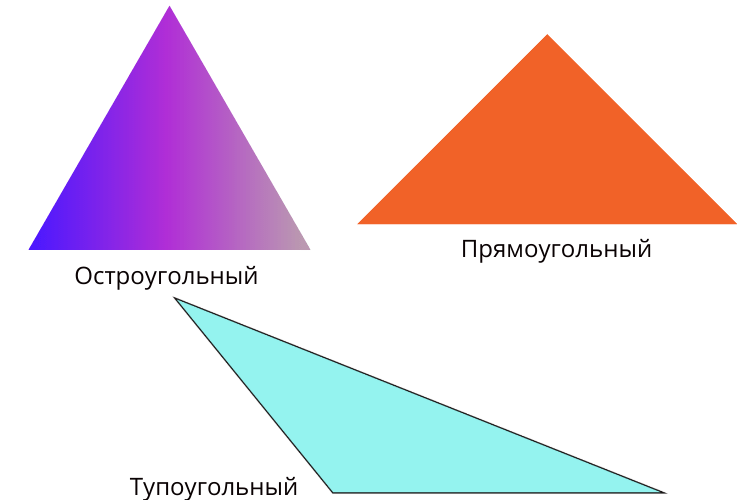
1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.

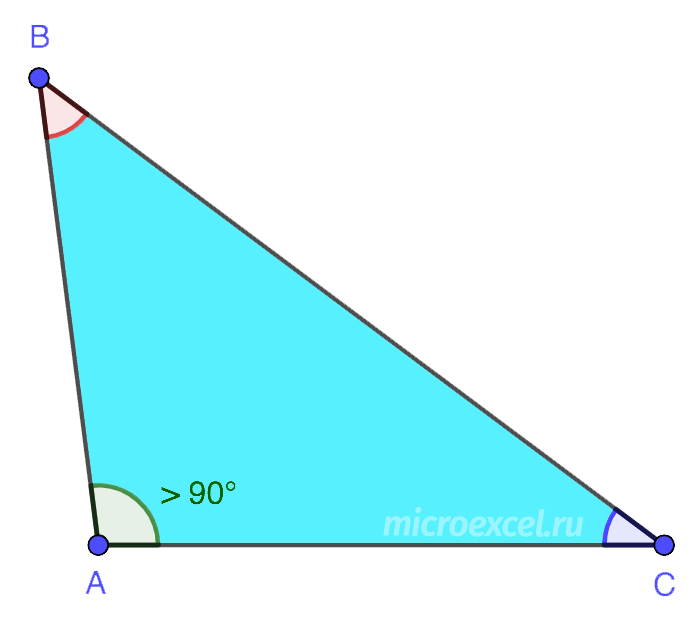
2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

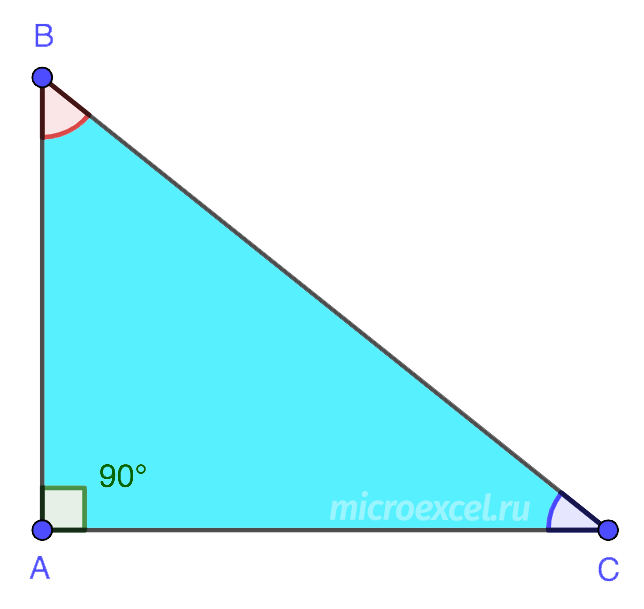
4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

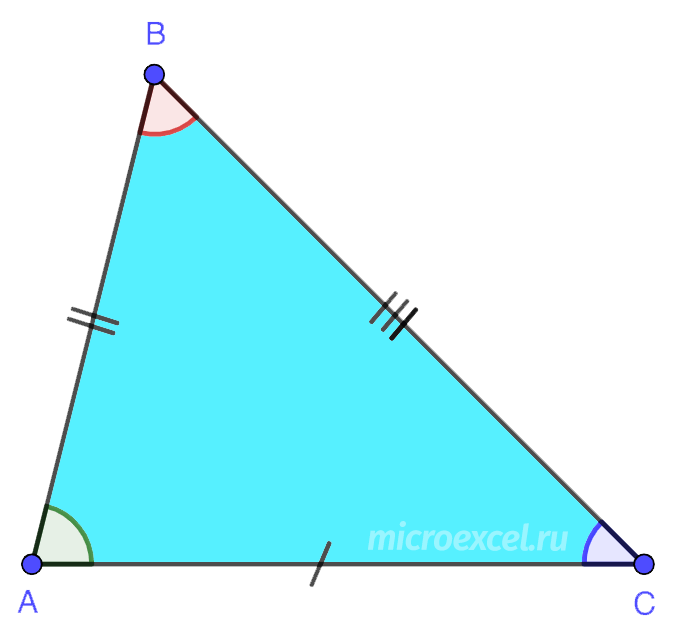
5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

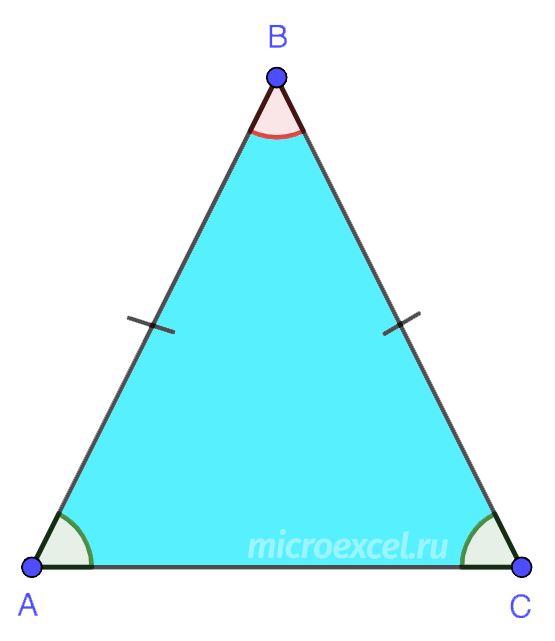
6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Виды треугольников по углам

Определение. Остроугольным треугольником называется треугольник, у которого все углы острые.

Определение. Прямоугольным треугольником называется треугольник с прямым углом.

Определение. Тупоугольным треугольником называется треугольник с тупым углом.

— Так, про треугольник понятно, — задумчиво сказал Бим. — Хотя — нет, не совсем понятно. Вот у этих конфет по 3 угла, но они разные.

— Конечно, — ответила Оля. — У всех этих конфет разные углы. Вот конфета, у которой все углы острые. Мы знаем, что острый угол меньше, чем прямой.

Оля достала листочек в клеточку и приложила к нему конфету.

 — Поглядите сюда. У клеточки одна сторона идет по горизонтали, а другая по вертикали. Если одну сторону конфеты приложить к горизонтали, то вторая сторона конфеты пойдет ниже вертикали клеточки, значит угол между сторонами треугольника острый. Проверим еще два угла, они оба острые. Все три угла — острые. Треугольник с тремя острыми углами называется остроугольным.

— Дай, пожалуйста, листочек в клеточку, — попросил Бим.

— С удовольствием, — ответила Оля.

Бим приложил другую конфету к листочку.

— Что-то у меня не получается. У конфеты два угла острых, а стороны третьего угла совпадают с вертикальной и горизонтальной сторонами клеточки…

— Так это уже другой вид треугольника — прямоугольный треугольник! — крикнул Коля. — Треугольник, у которого один угол прямой, называют прямоугольным.

Бом тоже попросил листочек в клеточку и приложил еще одну конфету.

— У меня совсем по-другому. В этой конфете сторона одного угла вообще в клеточку не попала, где-то вне клеточки. Что же это за угол такой?

— Такой угол называется тупым, он больше, чем прямой угол, — заметил Вася. — И треугольник, у которого есть тупой угол, называется тупоугольным треугольником.

Задача:

Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?

Решение:

Для решения данного задания нужно использовать неравенство a

Средняя оценка: 4.4 . Всего получено оценок: 160.

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

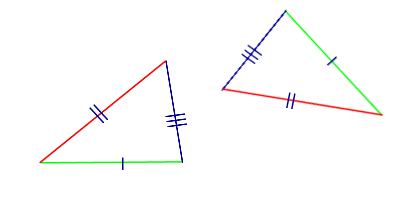
Отрезки равной длины на чертеже отмечают равным количеством черточек:

Свойства треугольников.

Меню

Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами.

Для инженера это еще и единственная «жесткая» плоская фигура на свете.

Раздел математики, посвященный изучению закономерностей треугольников — тригонометрия.

Сумма всех углов в треугольнике равна 180°.

[править] Точки и линии, связанные с треугольником

Есть сотни различных построений для определения особых точек внутри треугольника, которые удовлетворяют некоторым уникальным условиям. Часто необходимо построить три прямые, связанные аналогично с тремя сторонами (вершинами, углами) треугольника и тогда убедиться, что они пересекаются в одной точке. Важным инструментом для проверки этого является теорема Чевы, которая дает критерии для определения конкурентности прямых. Подобно этому, линии, связанные с треугольником часто строятся после проверки, три аналогичным образом полученные точки является коллинеарными — теорема Менелая дает для этого случая общий критерий. В этом разделе приведены только такие построения, которые наиболее часто встречаются.

Центр описанной окружности.

Срединный перпендикуляр треугольника — это перпендикуляр, который проходит посередине стороны треугольника. Три срединных перпендикуляра пересекаются в одной точке, которая является центром описанной окружности. Диаметр описанной окружности можно определить из теоремы синусов.

Исходя из теоремы Фалеса, можно утверждать, что если центр описанной окружности расположен на одной из сторон треугольника, тогда противоположный угол прямой. Более того, если центр описанной окружности находится внутри треугольника, то треугольник остроугольный, а если наружу, то треугольник тупоугольный.

Три высоты треугольника пересекаются в ортоцентре.

Высота треугольника — прямая, проведенная из вершины и перпендикулярная к противоположной стороне или к продолжению противоположной стороны. Эта сторона называется основанием треугольника. Точка пересечения стороны и перпендикуляра называется основой перпендикуляра. Длина высоты — это расстояние от вершины к основанию треугольника. Три высоты пересекаются в одной точке, которая называется ортоцентром треугольника. Ортоцентр лежит внутри треугольника (и соответственно все основания перпендикуляров лежат в треугольнике) тогда и только тогда, когда треугольник не тупоугольный.

На пересечении двух биссектрис треугольника находится центр вписанной окружности.

Биссектриса треугольника — это прямая, проведенная через вершину, которая делит соответствующий угол на две равные части. Три биссектрисы пересекаются в одной точке, инцентре, центре вписанной в треугольник окружности. Вписанная окружность — это круг, который лежит внутри треугольника и примыкает к трем его сторонам. Кроме того, есть еще три важных круга, внешние вписанные; они лежат за пределами треугольника и соприкасаются с одной его стороной, а также к продолжению других двух. Центры внутреннего и внешних вписанных кругов образуют ортоцентрическую систему.

Барицентр — центр масс треугольника.

Медиана треугольника — это прямая, проведенная через вершину и середину противоположной стороны и делящая треугольник на две одинаковых площади. Три медианы пересекаются в одной точке, которая называется центроидом треугольника. Эта точка также центр масс треугольника: если бы треугольник был сделан из дерева, то можно было бы держать равновесие держась за центроид. Центроид делит каждую медиану в соотношении 2:1, например расстояние между вершиной и центроидом вдвое больше, чем между центроидом и противоположной стороной.

Окружность девяти точек.

Средние точки трех сторон и основы трех высот лежат на одном круге, который называется кругом девяти точек треугольника. Остальные три точки, из-за которых круг получил свое название, это середины той части высоты, лежащей между ортоцентром и вершиной. Радиус окружности девяти точек равен половине описанной окружности. Она соприкасается со вписанной окружностью (в точке Фейербаха) и с тремя внешними вписанными кругами.

Равенство треугольников

Ну вот, а если не один, а два или больше треугольников. Как проверишь, равны ли они? Вообще-то по определению:

Но…это ужасно неудобное определение! Как, скажите на милость, накладывать два треугольника хотя бы даже в тетради?!

Но на наше счастье есть признаки равенства треугольников, которые позволяют действовать умом, не подвергая риску тетрадки.

Да и к тому же, отбросив легкомысленные шуточки, открою тебе секрет: для математика слово «наложить треугольники» означает вовсе не вырезать их и наложить, а сказать много-много-много слов, которые будeт доказывать, что два треугольника совпадут при наложении.

Так что ни в коем случае нельзя в работе писать «я проверил – треугольники совпадают при наложении» – тебе это не засчитают, и будут правы, потому что никто не гарантирует, что ты при наложении не ошибся, скажем, на четверть миллиметра.

Свойства и признаки равнобедренного треугольника

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Равнобедренный треугольник		Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Свойство	Углы при основании равнобедренного треугольника		Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Признак	Два равных угла треугольника	Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Свойство	Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника		В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.
Признак	Высота треугольника, совпадающая с медианой		Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Признак	Высота треугольника, совпадающая с биссектрисой		Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Признак	Биссектриса треугольника, совпадающая с медианой		Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

Определение: равнобедренный треугольник
	Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Свойство: углы при основании равнобедренного треугольника
	Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Признак: два равных угла треугольника
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.
Признак: высота треугольника, совпадающая с медианой
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Признак: высота треугольника, совпадающая с биссектрисой
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Признак: биссектриса треугольника, совпадающая с медианой
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

Определение равнобедренного треугольника

Определение: Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.

Свойство углов при основании равнобедренного треугольника

Свойство:Если треугольник является равнобедренным треугольником, то углы при его основании равны.

Признак равнобедренного треуголька: два равных угла треугольника

Признак:Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.

Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника

Свойство:В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.

Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой

Признак:Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным

Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой

Признак:Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным

Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой

Признак:Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

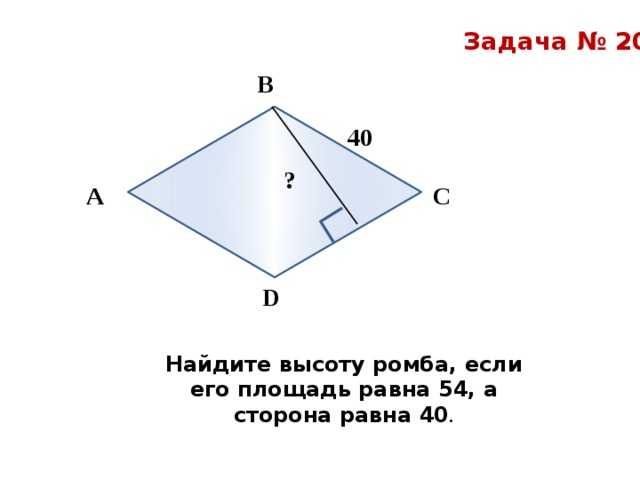
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Заключение

Вот какие вопросы написал Бим:

1. Треугольник — это …? Определение треугольника.
2. Какие бывают виды треугольников по углам?
3. Какие бывают виды треугольников по сторонам?

Ребята написали такие ответы:

1. Треугольник — это фигура из трех отрезков и трех углов.
2. Виды треугольников по углам: остроугольный, прямоугольный, тупоугольный.
3. Виды треугольников по сторонам: разносторонний треугольник, равнобедренный треугольник, равносторонний треугольник.

Теперь мы тоже будем знать, какие бывают виды треугольников по углам и сторонам.

Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).