Можно ли найти высоту ромба?

Что такое высота в географии?

Высота, как высота, это расстояние над уровнем моря. Области часто считаются «высотными», если они достигают не менее 2,400 метров (8,000 футов) в атмосферу. … С увеличением высоты атмосферное давление падает. Другими словами, если указанная высота велика, атмосферное давление низкое.

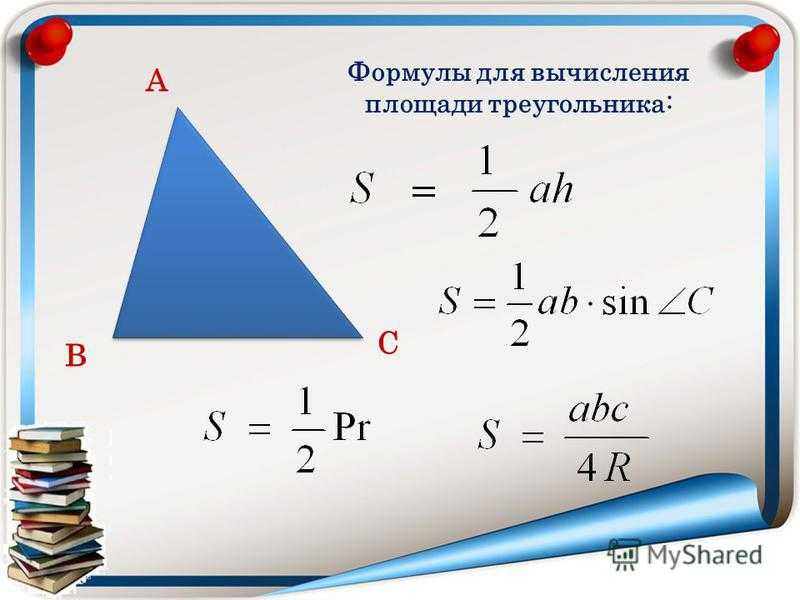
Какова высота треугольника класса 9? Высота кратчайшее расстояние от вершины до ее противоположной стороны. 3 высоты всегда встречаются в одной точке, независимо от формы треугольника. Точка, где встречаются 3 высоты, называется ортоцентром треугольника.

Длина и высота одинаковы?

Ответ проверен экспертом. Высота и высота одинакова для треугольника, В основном. Оба они относятся к длине перпендикуляра от вершины на противоположную сторону (основание). … Но высота всегда остается прежней.

В чем разница между высотой и длиной? Сравнение длины и высоты. Измерение объекта от одной точки до другой в той же плоскости называется длиной. Высота – это измерение объекта сверху вниз.

Какова высота треугольника класса 7?

Высота треугольника равна перпендикуляр, проведенный из вершины треугольника к противоположной стороне. Высота треугольника также известна как высота треугольника. В треугольнике ABC высота AD — это перпендикуляр, проведенный из вершины A в точку D на противоположной стороне BC.

Сколько высот может треугольник 1? Ответ: три

Треугольник имеет три высоты– один конец находится в вершине, а другой – на противоположной стороне.

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

r =	S
2 a

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

r =	√ S · sinα
2

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

r =	a · sinα
2

r =	a · sinβ
2

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

r =	d 1 · sin ( α /2)
2

r =	d 2 · sin ( β /2)
2

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

r =	d 1 · d 2
4 a

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Как вычислять площадь ромба, зная его сторону и радиус вписанной в него окружности?

Площадь ромба можно рассчитать, зная r – радиус и a – длину стороны фигуры. Уже известно, что S – площадь фигуры будет равна произведению b – стороны на h – высоту. Через центр окружности, он же будет являться и центром пересечения a, b – диагоналей ромба. Проведите высоту и одновременно диаметр ромба. На изображении видно, что высота фигуры – это два радиуса окружности. Теперь легко будет найти и площадь самого ромба:

S = a • h = a • 2r

Ниже смотрите пример задачи на данную тематику.

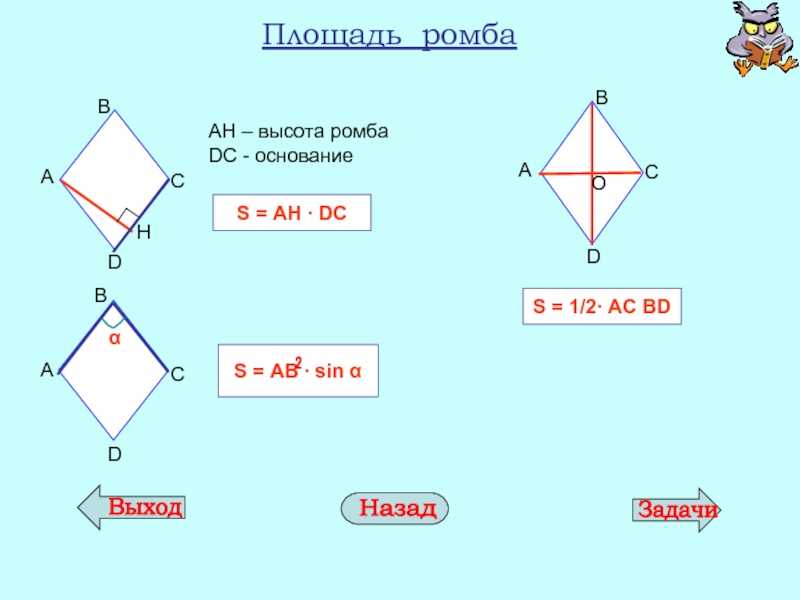
Площадь ромба

Еще смотрите подобные статьи на данную тематику здесь:

1. Площадь прямоугольника, как найти?
2. Как найти площадь круга?
3. Площадь квадрата – формулы.

Высота ромба через угол и противолежащую диагональ

Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.

Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:

С другой стороны (см. параграф 2):

Подставим (9) в (10):

Применяя формулу двойного угла для \(\small \sin \alpha, \) имеем: \(\small \sin \alpha=2 \cdot \sin \frac \cdot \cos \frac . \) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:

Варианты определения высоты

Если вам известно, чему равна сторона ромба (обозначается буквой а) и его площадь (S), вычислить высоту можно по простой формуле: h=S:a. Основная формула служит для определения площади: S=a*h.

Если для определения высоты по указанной выше формуле у вас не достает данных, вы можете воспользоваться некоторыми другими. Найдя с их помощью нужные значения, вы сможете подставить их в ту, по которой можно определить высоту.

Если вам известна длина диагоналей, вы легко найдете площадь. S=(d1*d2)/2.

Зная периметр ромба, можно найти длину его стороны: P=4a.

Еще одна формула для определения площади. S=a*a*sin (a).

Расшифровка:

• S — площадь ромба;
• a — длина стороны ромба;
• d1 — длина одной диагонали;
• d2 — длина второй диагонали;
• h — высота;
• Р — периметр;
• sin (a) — синус угла а.

Важно: существуют еще более сложные формулы, которые помогут определить дополнительные параметры. Как правило, в школьных задачах никто не предоставляет данные, по которым легко определить высоту ромба

Чтобы дать правильный ответ на поставленный вопрос, требуется применение нескольких формул. Совет: нарисуйте небольшую шпаргалку (ромб с обозначение сторон + формулы).

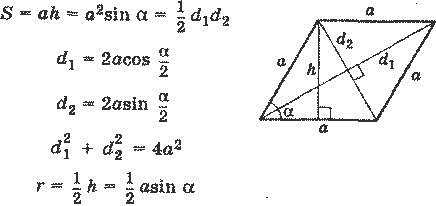
Можете также узнать косинус 210° градусов или sin(0°).

Формулы ромба

• Формулы площади ромба:
• Формула периметра ромба:

Ромб — это четырёхугольник, у которого все стороны равны. Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.

Формулы площади ромба:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади ромба выражается числом заключающихся в него квадратных единиц.

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d₁ — длина 1-ой диагонали

d₂ — длина 2-ой диагонали

Формула периметра ромба:

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).

P — периметр ромба

a — длина стороны ромба

Свойства ромба

Их пять и они перечислены ниже. Причем некоторые из них повторяют свойства параллелограмма, а какие-то присущи только рассматриваемой фигуре.

• Ромб — это параллелограмм, который принял особую форму. Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
• Диагонали этого четырехугольника пересекаются под углом, который равен 90º. Это удобно и во многом упрощает ход рассуждений при решении задач.
• Другое свойство диагоналей: каждая из них делится точкой пересечения на равные отрезки.
• Лежащие друг напротив друга углы у этой фигуры равны.
• И последнее свойство: диагонали ромба совпадают с биссектрисами углов.

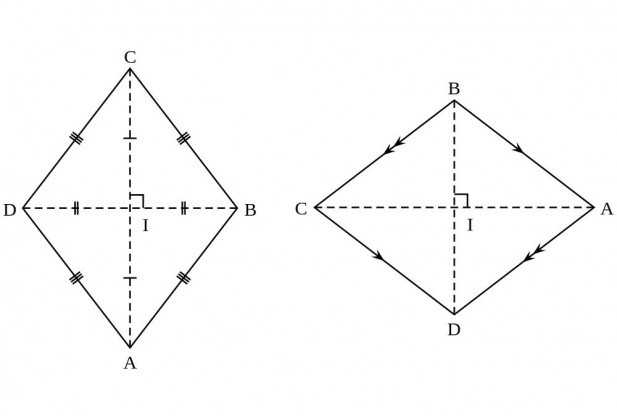
Как вычислить площадь ромба – свойства фигуры

Прежде, чем вычислить площадь ромба, лучше ознакомиться со свойствами данной фигуры. Ведь благодаря знанию этих характеристик дальше проще будет доказать вероятность той или иной формулы. Ранее упоминалось уже, что такое ромб. Он представляет собой фигуру с равными абсолютно всеми сторонами, равными противоположными острыми и тупыми углами, но не прямыми.

Ромб имеет следующие свойства:

• у него все стороны между собой равны
• углы, лежащие напротив друг друга, тоже равны
• диагонали данной фигуры являются биссектрисами, в точке пересечения делятся на равные отрезки
• также диагонали пересекаются в центре ромба и под прямыми углами
• противоположные стороны фигуры не могут пересекаться, даже если продлить лучи они же параллельны, как у параллелограмма.

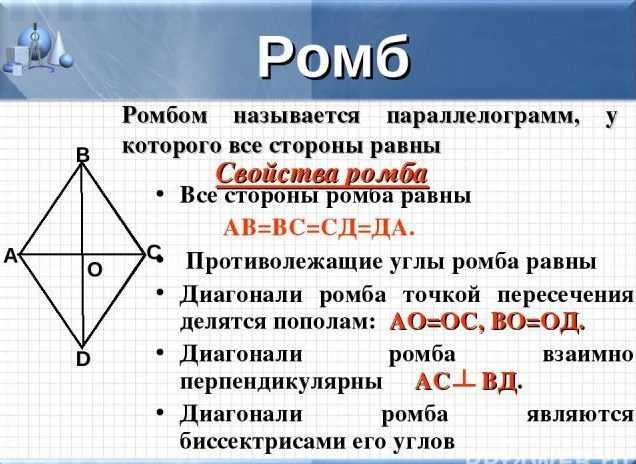
Свойства фигуры

Примеры возможных заданий

Задача 1

Одна из диагоналей ромба равна 8, а другая — 14 см. Требуется найти площадь фигуры и длину ее стороны.

Решение

Для нахождения первой величины потребуется формула 1, в которой Д₁ = 8, Д₂ = 14. Тогда площадь вычисляется так: (8 * 14) / 2 = 56 (см2).

Диагонали делят ромб на 4 треугольника. Каждый из них обязательно будет прямоугольным. Этим нужно воспользоваться, чтобы определить значение второй неизвестной. Сторона ромба станет гипотенузой треугольника, а катетами будут половины диагоналей.

Тогда а2 = (Д₁ /2)2 + (Д₂ /2)2. После подстановки всех значений получается: а2 = (8 / 2)2 + (14 / 2)2 = 16 + 49 = 65. Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.

Ответ: площадь 56 см2, а сторона 8,06 см.

Задача 2

Сторона ромба имеет значение, равное 5,5 дм, а его высота — 3,5 дм. Найти площадь фигуры.

Решение

Для того чтобы найти ответ нужна будет формула 2. В ней а = 5,5, Н = 3,5. Тогда, заменив в формуле буквы на числа, получим, что искомая величина равна 5,5 * 3,5 = 19,25 (дм2).

Ответ: площадь ромба равна 19,25 дм2.

Задача 3

Острый угол у некоторого ромба равен 60º, а его меньшая диагональ — 12 см. Требуется вычислить его площадь.

Решение

Чтобы получить результат, нужна будет формула под номером 3. В ней вместо А будет 60, а значение а неизвестно.

Для нахождения стороны ромба потребуется вспомнить теорему синусов. В прямоугольном треугольнике а будет гипотенузой, меньший катет равен половине диагонали, а угол делится пополам (известно из свойства, где упоминается биссектриса).

Тогда сторона а будет равна произведению катета на синус угла.

Катет нужно вычислить как Д/2 = 12/2 = 6 (см). Синус(А/2) будет равен его значению для угла 30º, то есть 1/2.

Выполнив несложные вычисления, получим такое значение стороны ромба: а = 3 (см).

Теперь площадь — это произведение 32 и синуса 60º, то есть 9 * (√3)/2 = (9√3)/2 (см2).

Ответ: искомая величина равна (9√3)/2 см2.

Примеры задач

Задание 1Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.

Решение:Используем первую формулу, рассмотренную выше: S = 10 см * 8 см = 80 см2.

Задание 2Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.

Решение:Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 * sin 30° = 36 см2 * 1/2 = 18 см2.

Задание 3Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.

Решение:Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 * 4 см * 8 см = 16 см2.

Как посчитать высоту ромба, если известна сторона и диагональ?

В этой задаче нужно использовать прямоугольный треугольник, который образован пересечением диагоналей.

Допустим, что сторона равна 10 см, а диагональ — 12 см.

Наши действия:

Находим размер половины второй диагонали при помощи теоремы Пифагора.
Гипотенуза в нашем случае — это сторона, потому величина половины диагонали будет равна разнице квадрата катета (10 в квадрате) и квадрата половины известной диагонали (6 в квадрате). Выходит, что нужно от 100 отнять 36 — имеем 64 сантиметра. Добываем корень из этого числа и получаем длину половины второй диагонали — 8 см. А полная длина равна 16 сантиметрам.

Подсчитываем площадь ромба при помощи двух диагоналей.
Умножаем длину первой диагонали (12 см) на длину второй (16 см) и делим это на 2 — получаем 96 см кв. (это площадь ромба).

Вычисляем высоту, зная размер стороны и площадь.
Для этого 96 поделите на 10 — выходит 9,6 сантиметров — это окончательный ответ.

Геометрическая фигура ромб представляет собой вариацию параллелограмма, имеющего равные стороны. Его высотой является часть прямой, проходящая через вершину фигуры и образующая при пересечении с противолежащей стороной угол 90°. Частным случаем ромба является квадрат. Знание свойств ромба, а также верная графическая интерпретация условия задачи позволяют правильно определить высоту фигуры, используя один из допустимых способов.

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами
. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.

Как находить высоту ромба

Четырёхугольники — это такие фигуры, у которых могут изменяться углы при неизменных длинах сторон. Поэтому, в отличие от треугольника, мало знать длины сторон четырёхугольника, необходимо указывать ещё и размеры углов или высоту. Например, если углы ромба равны 90°, то получится квадрат. В этом случае высота совпадает со стороной. Рассмотрим, как найти высоту ромба при углах, отличных от прямых.

Определяем величину двух высот ромба, опущенных из одного угла

Имеем ромб ABCD, у которого AB//CD, BC//AD, АВ = ВС = СD = DА = а. Высотой h называется перпендикуляр, опущенный из угла на противоположную сторону. Опустим высоту АН на сторону ВС, а другую высоту АН1 опустим из того же угла на сторону DС.

• Тогда высота АН = AB × sin∟B;
• Высота AH1 = AD × sin∟D.

Одно из свойств ромба — равенство противоположных углов, т.е. ∟B = ∟D. Поскольку АВ = AD (все стороны ромба все равны между собой), то высота АН = АН1. Аналогично можно доказать, что две высоты, опущенные из любого угла, равны между собой.

Как соотносятся остальные высоты ромба между собой

Поскольку противоположные стороны параллельны, то сумма углов, примыкающих к одной стороне, равна 180°. Следовательно, синусы всех четырёх углов равны между собой:

sin∟D = sin(180° — ∟D) = sin∟С = sin∟А = sin∟В.

Следовательно, все высоты, опущенные из любого угла ромба, равны между собой, а сторона, угол и высота связаны между собой жёстким соотношением: h = a × sin∟A, где а — длина любой стороны, ∟A — любой угол ромба.

Зная диагонали, найти высоту ромба легко. В этом нам поможет теорема Пифагора.
И хоть она касается прямоугольных треугольников, в ромбе они тоже есть — их образует пересечение двух диагоналей d1 и d2:

Вообразим, что диагональ 1 равна 30 сантиметрам, а диагональ 2 — 40 см.

Итак, наши действия:

Подсчитываем величину стороны по теореме Пифагора.
Сторона BC — это гипотенуза (потому что лежит напротив тупого угла) треугольника BXD (X — это пересечение диагоналей d1 и d2). А значит размер этой стороны в квадрате равен сумме квадратов сторон BX и XC. Их размер нам тоже известен (диагонали ромба пересечением делятся пополам) — это 20 и 15 сантиметров. Выходит, что длина стороны BC равняется корню от 20 в квадрате и 15 в квадрате. Сумма квадратов диагоналей равняется 625, а если извлечь это число из корня, получаем размер катета, равный 25 сантиметрам.

Вычисляем площадь ромба при помощи двух диагоналей.
Для этого умножаем d1 на d2 и делим результат на 2. Получается: 30 умножить на 40 (= 1200) и поделить на 2 — выходит 600 см кв. — это и есть площадь ромба.

Теперь вычисляем высоту, зная длину стороны и площадь ромба.
Для этого нужно площадь поделить на длину катета (это и есть формула вычисления высоты ромба): 1200 делим на 25 — выходит 48 сантиметров. Это окончательный ответ.