Как найти коэффициент жёсткости пружины, используя формулу для расчёта

Применение цилиндрических пружин

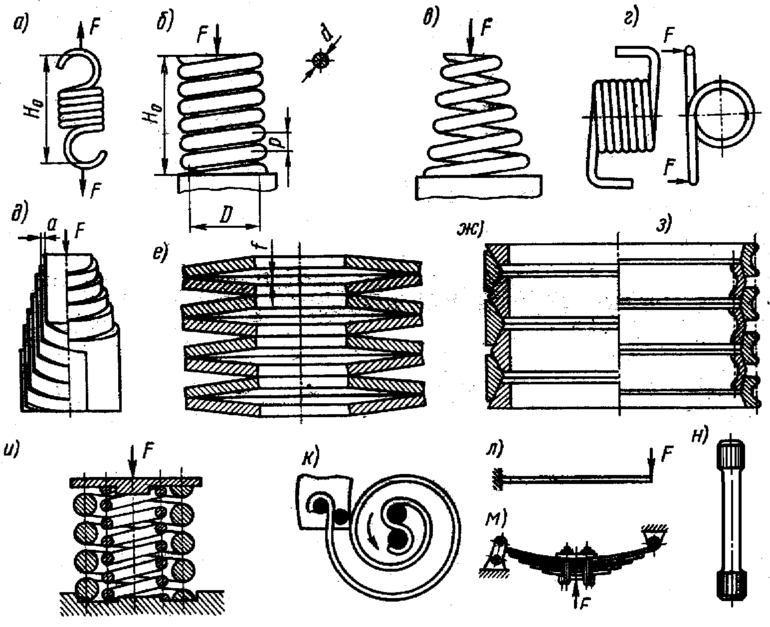
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.

Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.

Главными параметрами изделия считаются:

малый, средний и большой диаметр витков и самой проволоки;
шаг размещения отдельный колец.

В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:

Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.

Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.

Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.

Практические занятия

Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.

Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.

На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:

k — суммарная жёсткость соединений;
k1 …ki — жёсткость каждого элемента системы;
i — число пружин в цепи.

Основная методика для вычислений

На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:

Пружина фиксируется вертикально. Для этого используется любая удобная опора со свободной нижней частью.
Линейкой измеряется длина предмета. Результат записывается как х1.
На свободный конец подвешивается груз с известной массой m.
Измеряется длина изделия под воздействием амплитуды. Вывод записывается как х2.
Производит подсчёт абсолютного удлинения: x = x2-x1. Для определения энергии (силы) и k в международной системе СИ осуществляется перевод длины из разных единиц измерения в метры.
Сила, спровоцировавшая деформацию, считается силой тяжести тела. Она рассчитывается по формуле: F = mg, где м является массой используемого груза (вес переводится в килограммы), а g (равен 9,8) — постоянная величина, с помощью которой отмечается ускорение свободного падения.

Решение задач

Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.

Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.

Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.

Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.

Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.

Вычисление коэффициента жесткости опытным методом

С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:

линейка;
пружина;
груз с известной массой.

Последовательность действий для опыта такова:

Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
При помощи линейки измеряется ее длина и записывается как величина x1.
На свободный конец нужно подвесить груз с известной массой m.
Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.

Примеры задач на нахождение жесткости

Задача 1

На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.

Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.

Ответ: жесткость пружины составит 2500 Н/м.

Задача 2

Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.

Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.

Ответ: во втором случае пружина растянется на 10 см.

Новости сайта

Виртуальная лабораторная работа МЭШ по физике

Приложение моделирует эксперимент по превращению льда в пар. Целью работы является определение коэффициента полезного действия тепловой установки. Виртуальная лабораторная установка …

(115 words)

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике В приложении представлена интерактивная модель экспериментальной установки для нахождения массы воды в мокром снеге. Для нахождения искомой величины требуется поместить мокрый снег в …

(45 words)

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике В приложении представлена виртуальная лабораторная установка для определения длины световой волны с помощью дифракционной решетки. Приложение может быть использовано в качестве …

(51 words)

(0 replies so far)

Виртуальная лабораторная работа по физике В приложении представлена модель лабораторной работы по физике «Определение удельной теплоты плавления льда». Установка работает в режиме реального времени под управлением электронного блока. Порядок …

(129 words)

(0 replies so far)

Виртуальная лабораторная работа по физике Приложение моделирует эксперимент по определению удельной теплоемкости жидкостей методом электрокалориметра. Виртуальная лабораторная установка работает в режиме реального …

(32 words)

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике Представленное приложение моделирует одноименную лабораторную установку, описанную в учебнике физики за 7 класс под авторством Перышкина А.В.

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике Приложение моделирует эксперимент по определению удельной теплоемкости металлов. Виртуальная лабораторная установка работает в режиме реального времени и является интерактивной.

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике Приложение моделирует эксперимент по определению удельной теплоты парообразования воды. Виртуальная лабораторная установка работает в режиме реального времени и является интерактивной.

(0 replies so far)

Виртуальная лабораторная работа МЭШ по физике

Приложение моделирует реальный эксперимент по определению постоянной Больцмана. Виртуальная лабораторная установка работает в режиме реального времени и является многовариантной.

(0 replies so far)

Виртуальная лабораторная работа по физике

Приложение моделирует одноименную лабораторную работу по физике за 8 класс под авторством Перышкина А.В. Виртуальная лабораторная установка работает в режиме реального времени и …
(66 words)

(0 replies so far)

Коэффициент жесткости пружины

Определение

Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.

Применяется в механике твердого тела в разделе упругости.

Формула расчета через массу и длину

Используя закон Гука, коэффициент жесткости можно вычислить по формуле:

\(k\;=\;\frac Fx\)

Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:

\(F\;=\;m\;\times\;g\)

где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.

Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.

При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:

\(\frac1k\;=\;(\frac1{k_1}\;+\;\frac1{k_2}\;+\;…\;+\;\frac1{k_n})\)

От чего зависит жесткость

Жесткость пружины зависит от нескольких параметров:

геометрии пружины;
типа материала;
коэффициента;
срока эксплуатации.

Геометрия пружины

На жесткость витой пружины влияет:

количество витков;
их диаметр;
диаметр проволоки.

Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.

Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.

Их основные геометрические параметры:

количество витков;
количество волн на виток;
сечение ленты.

Тип материала

У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.

Определение

Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.

Предел упругости измеряют в паскалях и определяют по формуле:

\(\sigma_{у\;}=\;\frac FS\)

где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.

Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие. Все они взаимосвязаны, поэтому, выяснив значение одной из величин с помощью справочной таблицы, можно вычислить другие.

Коэффициент

Определение

Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.

Эта линейная зависимость описывается формулой:

\(F=\;k\;\times\;x\)

где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.

Примечание

Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.

Срок эксплуатации

Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.

Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство. В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.

Лабораторная работа № 2 «Измерение жесткости пружины»

Решебник по физике за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год), задача №2 к главе «ЛАБОРАТОРНЫЕ РАБОТЫ».

Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести

уравновешивающей силу упругости на основе закона Гука:

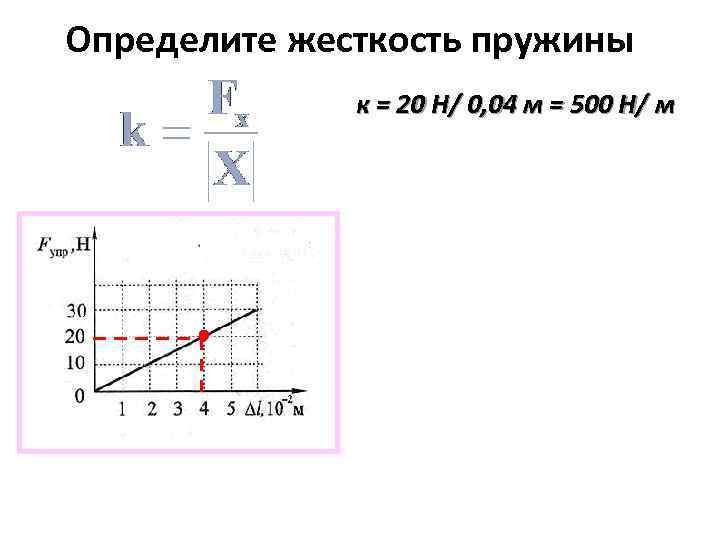
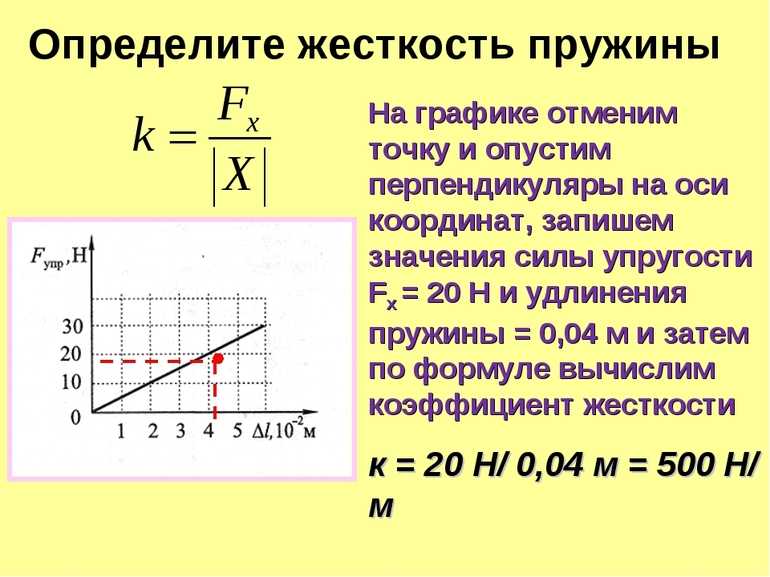
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F_упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

Результат измерения обычно записывается в виде выражения k = = k_cp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε_k) равна отношению абсолютной погрешности Δk к значению величины k:

откуда Δk — ε_kk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе

Средства измерения: 1) набор грузов, масса каждого равна m = 0,100 кг, а погрешность Δm = 0,002 кг; 2) линейка с миллиметровыми делениями.

Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.

Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:

6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k_cp.

7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k_ср (из опыта с одним грузом). В формуле (1)

так как погрешность при измерении удлинения Δx=1 мм, то

и запишите ответ в виде:

1 Принять g≈10 м/с 2 .

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:

где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m = (0,1±0,002) кг.

Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Суть метода заключается в том, что пружину нагружают силой определенной величины (в нашем случае, вес груза)

Дожидаются наступления статического равновесия пружины и замеряют ее деформацию под воздействием этой силы

Величина коэффициента жесткости

Далее определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости по следующим принципам

, (12)

, (13)

где , , , , , – максимальные и минимальные значения величин, задействованных в формулах.

Затем, поскольку коэффициент жесткости распределяется по симметричному «нормальному закону», по формулам, приведенным ниже для величин, определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата

(14)

(15)

. (16)

Определение коэффициента жесткости пружины методом строительной механики

Коэффициент жесткости определяется по зависимости

. (17)

С использованием формулы 17, а также зависимостей 12 и 13 определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости.

Затем, по формулам 14, 15 и 16 определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата.

ИТОГИ ЛАБОРАТОРНОЙ РАБОТЫ И ОФОРМЛЕНИЕ ОТЧЕТА

Итоги лабораторной работы

Анализируя полученные результаты необходимо сравнить методы определения коэффициента жесткости по критериям точности и сложности. Далее, дать оценку точности и достоверности полученных результатов, а также предложить меры по повышению точности результатов в случае неудовлетворительности последних.

Оформление отчета

Оформляется один отчет на бригаду на листах формата А4.

В отчете должны быть приведены все необходимые данные, расчеты и пояснения, результаты и выводы.

Отчет должен содержать следующие обязательные элементы: титульный лист с фамилиями выполнявших работу и проверяющего, оглавление с указанием номеров страниц начала разделов, нумерацию страниц, и разделы в следующем порядке:

1) исходные данные (см. п. 2.3),

2) определение статистических оценок измеренных величин,

3) определение коэффициента жесткости пружины статическим методом,

4) определение коэффициента жесткости пружины методом строительной механики,

Все появляющиеся первый раз переменные должны быть сопровождены пояснениями. Например,

деформация пружины – или

или

–модуль упругости стали при сдвиге.

У всех значений величин, имеющих размерность, должны стоять соответствующие единицы измерения. Все формулы должны быть раскрыты и сосчитаны. Например,

=176-138=38 мм.

Все рисунки и таблицы должны иметь названия и сквозную нумерацию.

СПИСОК ЛИТЕРАТУРЫ

1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1962. – 576 с.

2. ГОСТ 24026-80 Исследовательские испытания. Планирование эксперимента. Термины и определения.

3. Налимов В. В. Теория эксперимента – М.: Наука, 1971. – 207 с.

4. Румшиский Л.3. Математическая обработка результатов эксперимента – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1971. – 192 с.

Приложение

	0.9	0.95	0.98	0.99	0.999
2.132	2.776	3.747	4.604	8.610
2.015	2.571	3.365	4.032	6.859
1.943	2.447	3.143	3.707	5.959
1.895	2.365	2.998	3.499	5.405
1.860	2.306	2.896	3.355	5.041
1.833	2.262	2.821	3.250	4.781
1.812	2.228	2.764	3.169	4.587
1.796	2.201	2.718	3.106	4.487
1.782	2.179	2.681	3.055	4.318
1.771	2.160	2.650	3.012	4.221
1.761	2.145	2.624	2.977	4.140
1.753	2.131	2.602	2.947	4.073
1.746	2.120	2.583	2.921	4.015
1.734	2.103	2.552	2.878	3.922
1.725	2.086	2.528	2.845	3.850
1.708	2.060	2.485	2.787	3.725
1.697	2.042	2.457	2.750	3.646
1.689	2.030	2.437	2.724	3.591
1.684	2.021	2.423	2.704	3.551
1.679	2.014	2.412	2.689	3.522
1.676	2.008	2.403	2.677	3.497
1.671	2.000	2.390	2.660	3.460
1.667	1.995	2.381	2.648	3.436
1.664	1.990	2.374	3.639	3.416
1.662	1.987	2.368	2.632	3.401
1.660	1.984	2.364	2.626	3.391
	1.645	1.960	2.326	2.576	3.291