Площади фигур (плоских и объемных)

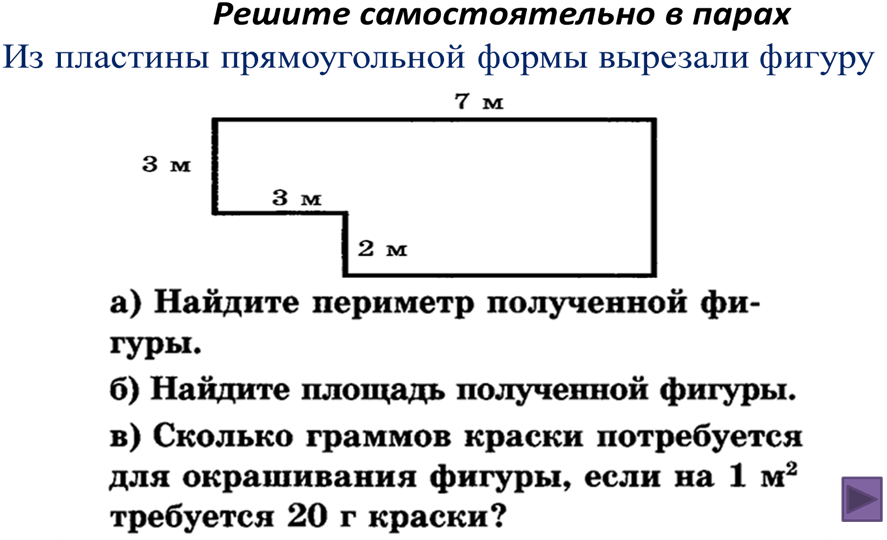
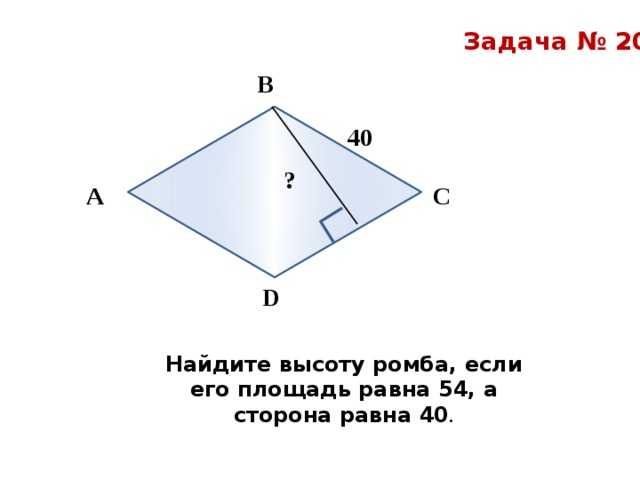
Вычисление площадей фигур, изображенных на клетчатой бумаге

При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?

Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.

Возможны следующие случаи.

1. Фигура представляет собой треугольник, параллелограмм, трапецию:

Какой способ лучше?

Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.

Вот смотри, нужно посчитать площадь такой фигуры:

Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.

А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).

\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле). \( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\)

\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).

\( \displaystyle S=66-12-10-5-5,5=33,5\)Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?

Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.

С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.

Теоретическая часть

Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Уже эта простая решетка послужила К. Гауссу отправной точкой для сравнения площади круга с числом точек с целыми координатами, находящихся внутри него. То, что некоторые простые геометрические утверждения о фигурах на плоскости имеют глубокие следствия в арифметических исследованиях, было в явном виде замечено Г. Минковским в 1896 г., когда он впервые для рассмотрения теоретико-числовых проблем привлек геометрические методы .

Нарисуем на клетчатой бумаге какой-нибудь многоугольник (Приложение 1, рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты.

Использованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (Приложение 2, рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.

Однако оказывается, что есть очень простая формула, позволяющая вычислить площади таких многоугольников с вершинами в узлах квадратной сетки.

Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика.

Эта формула оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.

Она является классическим результатом комбинаторной геометрии и геометрии чисел.

Доказательство формулы Пика

Пусть АВСD
– прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (Приложение 3, рисунок 3).

Обозначим через В — количество узлов, лежащих внутри прямоугольника, а через Г — количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки

вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S
равна

S

= В +
+ 4 ·
= В +
— 1 .

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S
= В + — 1 .
Это и есть формула Пика.

Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Теорема Пика

Формула

Пусть дан некоторый решётчатый многоугольник, с ненулевой площадью.

Обозначим его площадь через ; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через ; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через .

Тогда справедливо соотношение, называемое формулой Пика:

В частности, если известны значения I и B для некоторого многоугольника, то его площадь можно посчитать за , даже не зная координат его вершин.

Это соотношение открыл и доказал австрийский математик Георг Александр Пик (Georg Alexander Pick) в 1899 г.

Единичный квадрат. В самом деле, для него , , , и формула верна.

Произвольный невырожденный прямоугольник со сторонами, параллельными осям координат. Для доказательства формулы обозначим через и длины сторон прямоугольника. Тогда находим: , , . Непосредственной подстановкой убеждаемся, что формула Пика верна.

Прямоугольный треугольник с катетами, параллельными осям координат. Для доказательства заметим, что любой такой треугольник можно получить отсечением некоторого прямоугольника его диагональю. Обозначив через число целочисленных точек, лежащих на диагонали, можно показать, что формула Пика выполняется для такого треугольника, независимо от значения .

Произвольный треугольник. Заметим, что любой такой треугольник может быть превращён в прямоугольник приклеиванием к его сторонам прямоугольных треугольников с катетами, параллельными осям координат (при этом понадобится не более 3 таких треугольников). Отсюда можно получить корректность формулы Пика для любого треугольника.

Произвольный многоугольник. Для доказательства триангулируем его, т.е. разобьём на треугольники с вершинами в целочисленных точках. Для одного треугольника формулу Пика мы уже доказали. Дальше, можно доказать, что при добавлении к произвольному многоугольнику любого треугольника формула Пика сохраняет свою корректность. Отсюда по индукции следует, что она верна для любого многоугольника.

Обобщения

Возможны обобщения теоремы Пика на непростые многоугольники, но они более сложные и требуют больше информации, чем просто количество внутренних и граничных вершин. Например, многоугольник с отверстиями, ограниченными простыми целочисленными многоугольниками, не пересекающимися друг с другом и с границей, имеет площадь
час{\ displaystyle h}

Азнак равноя+б2+час-1.{\ displaystyle A = i + {\ frac {b} {2}} + h-1.}

плоскими прямолинейными графамиэйлеровой характеристикивитков

Тетраэдры Рив в трех измерениях имеют четыре целых точек как вершины и не содержат другие целые точек. Однако не все они имеют одинаковую громкость. Следовательно, не может быть аналога теоремы Пика в трех измерениях, который выражает объем многогранника как функцию только количества его внутренних и граничных точек. Однако вместо этого эти объемы можно выразить с помощью полиномов Эрхарта .

Как найти площадь геометрической фигуры по клеточкам?

Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.

Площадь фигуры по клеточкам

Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел — это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

N — количество узлов, которые находятся внутри фигуры.

M — количество узлов, которые находятся на границах (на вершинах и сторонах).

Примеры нахождения площади по клеточкам

1) Найдём площадь треугольника. Будем считать, что одна клетка — это 1 см.

Отметим внутренние узлы и узлы, которые находятся на границах.

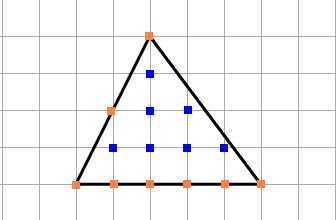
N = 7 (внутренние).

M = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 — 1 = 10 см².

2) Найдём площадь трапеции по клеточкам, одна клетка — это 1 см. Отметим все узлы и подсчитаем их количество.

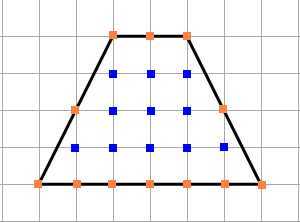
N = 11 (внутренние).

M = 12 (узлы на границах).

Площадь трапеции S = 11 + 12/2 — 1 = 16 см².

3) Найдём площадь произвольного многоугольника. Одна клетка — это 1 см.

Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.

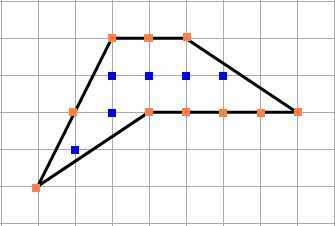
N = 6 (внутренние узлы).

M = 8 (узлы на границах).

Площадь многоугольника S = 6 + 10/2 — 1 = 10 см².

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle {{S}_{ASB}}\).

И тогда

\( \displaystyle {{S}_{полн. пов.\ \ }}=3{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)Вспомним теперь, что

\( \displaystyle {{S}_{осн}}\) — это площадь правильного треугольника \( \displaystyle ABC\).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \).

У нас «\( \displaystyle a\)» — это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60{}^\circ =\frac{\sqrt{3}}{2}\).

Значит, \( \displaystyle {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\frac{\sqrt{3}}{2}=\frac{{{a}^{2}}\sqrt{3}}{4}\).

Теперь найдем \( \displaystyle {{S}_{\Delta ASB}}\).

Пользуясь основной формулой площади и теоремой Пифагора, находим

\( \displaystyle {{S}_{\Delta ASB}} = \frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:. \( \displaystyle S={{a}^{2}}\sqrt{3}\)

\( \displaystyle S={{a}^{2}}\sqrt{3}\).

Важное замечание по площадям

Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю
. Получим:

Числа n
и k
— это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью вида ***,5. Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Формула

Предположим, что у многоугольника есть целые координаты всех его вершин. Позвольте быть количеством целочисленных точек, которые являются внутренними по отношению к многоугольнику, и позвольте быть количеством целочисленных точек на его границе (включая вершины, а также точки вдоль сторон многоугольника). Тогда площадь этого многоугольника равна:
я{\ displaystyle i}б{\ displaystyle b} А{\ displaystyle A}

Азнак равноя+б2-1.{\ displaystyle A = i + {\ frac {b} {2}} — 1.}

язнак равно7{\ displaystyle i = 7}бзнак равно8{\ displaystyle b = 8}Азнак равно7+82-1знак равно10{\ displaystyle A = 7 + {\ tfrac {8} {2}} — 1 = 10}

Нахождение площади фигур геометрическим методом и по формуле Пика

Я решила убедиться в том, что формула Пика верна для всех рассмотренных примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Я рассмотрела некоторые задачи на клетчатой бумаге с клетками размером 1 см1 см и провела сравнительный анализ по решению задач (Таблица№1).

Таблица№1 Решение задач различными способами.

Рисунок

По формуле геометрии

По формуле Пика

Задача №1

S=S

пр
-(2S

+2S

)

пр
=4*5=20

см
2

=(2*1)/2=1

см
2

=(2*4)/2=4

см
2

S=20-(2*1+2*4)=10

см
2

Ответ
:10

см
².

В = 8, Г = 6

= 8 + 6/2 – 1 = 10 (см²)

Ответ: 10 см².

Задача №2

a=2, h=4

S=a*h=2*4=8

см
2

Ответ
: 8

см
².

В = 6, Г = 6

= 6 + 6/2 – 1 = 8 (см²)

Ответ: 8 см².

Задача №3

S=S

кв
-(S

+2S

)

кв
=4

=16

см
2

1
=(3*3)/2=4,5см
2

2
=(1*4)/2=2см
2

=16-(4,5+2*2)=7.5 см
2

В = 6, Г = 5

= 6 + 5/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Задача №4

S=S

пр
-(S

)

пр
=4

3=12

см
2

=(3*1)/2=1,5

см
2

=(1*2)/2=1

см
2

=(1+3)*1/2=2

см
2

S=12-(1,5+1+2)=7.5

см
2

В = 5, Г = 7

= 5 + 7/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Задача №

5.

S=S

пр
-(S

)

пр
=6

5=30

см
2

=(2*5)/2=5

см
2

=(1*6)/2=3

см
2

=(4*4)/2=8

см
2

S=30-(5+3+8)=14

см
2

Ответ: 14 см²

В = 12, Г = 6

= 12 + 6/2 – 1 = 14 (см²)

Ответ: 14 см²

Задача

№6.

тр
=(4+9)/2*3=19,5 см
2

Ответ: 19,5 см
2

В = 12, Г = 17

= 12 + 17/2 – 1 = 19,5 (см²)

Ответ: 19,5 см
2

Задача

№7.

Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м

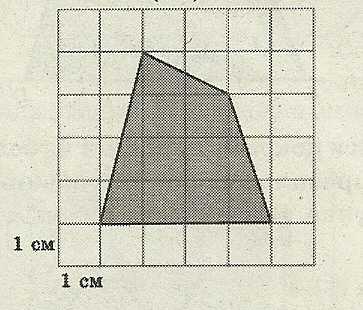
S= S

=(800*200)/2=80000

м
2

=(200*600)/2=60000

м
2

=(800+600)/2*400=

280000

м
2

80000+60000+240000=

420000м
2

Ответ: 420 000 м²

В = 8, Г = 7.
S

= 8 + 7/2 – 1 = 10,5 (см²)

1 см² — 200² м²;
S

= 40000 · 10,5 = 420 000 (м²)

Ответ: 420 000 м²

Задача №8

. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе

1 см – 200 м.

=
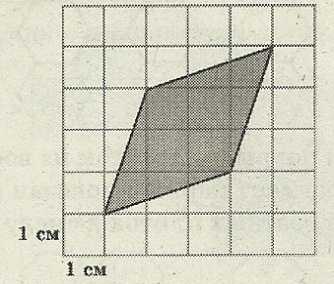
S

кв
-2(S

тр
+
S

трап
)

кв
=800
*
800=640000 м
2

тр
=(200*600)/2=60000м
2

трап
=(200+800)/2*200=

100000м
2

=640000-2(60000+10000)=

320000 м
2

Ответ: 320 000 м²

Решение.

Найдём
S

площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика:
S

= В +
— 1

В = 7, Г = 4.
S

= 7 + 4/2 – 1 = 8 (см²)

1 см² — 200² м²;
S

= 40000 · 8 = 320 000 (м²)

Ответ: 320 000 м²

Задача №9

. Найдите площадь
S

сектора, считая стороны квадратных клеток равными 1. В ответе укажите
.

Сектор является одной четвертой частью круга и, следовательно, его площадь равна одной четвертой площади круга. Площадь круга равна π
R

2

, где
R

– радиус круга. В нашем случае
R

=√5

и, следовательно, площадь
S

сектора равна 5π/4. Откуда
S

/π=1,25.

Ответ. 1,25.

Г= 5, В= 2,
S

= В + Г/2 – 1= 2 + 5/2 – 1= 3,5,
≈ 1,11

Ответ. 1,11.

Задача №10.

Найдите площадь
S

кольца, считая стороны квадратных клеток равными 1. В ответе укажите
.

Площадь кольца равна разности площадей внешнего и внутреннего кругов. Радиус
R

внешнего круга равен

2
, радиус
r

внутреннего круга равен 2. Следовательно, площадь кольца равна 4
и, следовательно,
. Ответ:4.

Г= 8, В= 8,
S

= В + Г/2 – 1= 8 + 8/2 – 1=11,
≈ 3,5

Ответ:3,5

Выводы: Рассмотренные задания аналогичны заданию из вариантов контрольно-измерительных материалов ЕГЭ по математике (задачи №5,6),.

Из рассмотренных решений задач я увидела, что некоторые из них, например задачи № 2,6, легче решить, применяя геометрические формулы, так как высоту и основание можно определить по рисунку. Но в большинстве задач требуется разбиение фигуры на более простые (задача №7) или достраивание до прямоугольника (задачи №1,4,5), квадрата (задачи №3,8).

Из решения задач №9 и №10 я увидела, что применение формулы Пика к фигурам, которые не являются многоугольниками, даёт приближённый результат.

Для того, чтобы проверить рациональность применения формулы Пика, я провела исследование на предмет затраченного времени (Приложение 4, таблица №2).

Вывод: из таблицы и диаграммы (Приложение 4, диаграмма 1) видно, что при решении задач с помощью формулы Пика, времени затрачивается гораздо меньше.

Площадь сложных фигур — Памятки по математике — Памятки ученикам

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

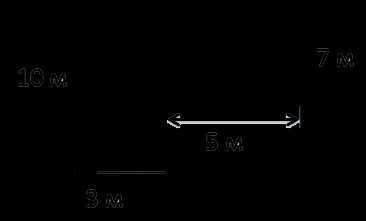
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

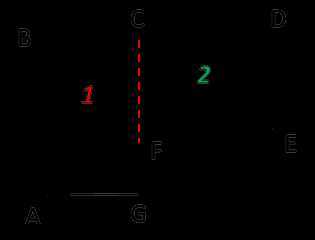_ABCE_EFKL2_CDEF_CDEF2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.

_ABCE_EFKL2

Ответ: S = 65 м2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD.

Вначале найдём площадь прямоугольника по формуле.

_ABCD_ABCD2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см2

S_ABC = S_ACD = 10 см2.

Способ 2. Дострой до прямоугольника и вычти лишнее

Очень удобен для сложных фигур, но и для простых неплох

Достроить искомую фигуру до прямоугольника;
Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
Из площади прямоугольника вычесть сумму площадей всех лишних фигур.

Давай посчитаем площадь того же треугольника вторым способом.

Нужно окружить нашу фигуру прямоугольником. Вот так:

Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!

Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:

ПЛОЩАДИ ПЛОСКИХ ФИГУР

Способы нахождения площади фигур на клетчатой бумаге:

Способ 1. Считай клетки и применяй формулы

Удобен для стандартных фигур: треугольника, трапеции и т.д.

Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
Подставить найденные значения в уравнение площади.

Способ 2. Дострой до прямоугольника и вычти лишнее

Очень удобен для сложных фигур, но и для простых неплох

Достроить искомую фигуру до прямоугольника;
Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
Из площади прямоугольника вычесть сумму площадей всех лишних фигур.

Способ 3. Формула Пика

Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.

Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.

В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.