Нахождение координат середины отрезка, примеры, решения

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Точки a и b введены! Решение:

Даны точки a =

и b =

Найдем расстояние между точками (s)

Отрезком
называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.

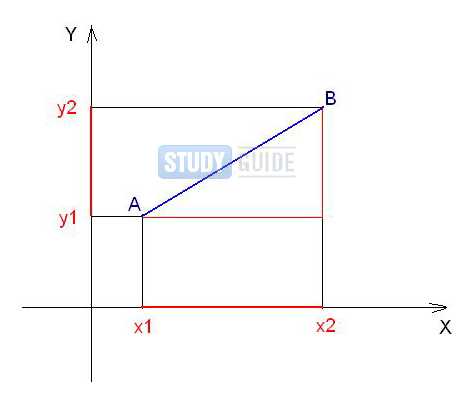
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов
(x1; y1)

и
(x2; y2)

. На оси
X

и
Y

из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y

длина проекции равна y2-y1

, а на ось Х

длина проекции равна x2-x1

. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)²

. В данном случае |AB|

является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3)

и (2;5)

. Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5

. А это значит, что длина нашего отрезка равна 5:1/2

.

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

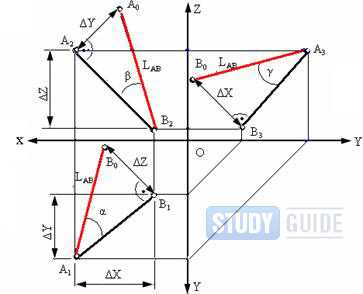
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y)

исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1

.

Рассчитаем длину отрезка А

, для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²)

.

Если наш отрезок расположен между точками, координаты которых 2;4

и 4;1

, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61

.

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.

Метод координат в пространстве

Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?

1. Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
2. После этого нужно возвести каждую координату вектора в квадрат.
3. Затем складываем квадраты координат.
4. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).

Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.

Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим. Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче

Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение:
по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём
– вынесение множителя из-под корня. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно)

Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате: Готово.

Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.

Векторное произведение векторов

И если скалярным произведением двух векторов и будет число, то векторным произведением двух векторов \( \vec{a}\) и \( \vec{b}\) будет вектор \( ~\vec{c}=\vec{a}\cdot \vec{b}\), причем данный вектор будет перпендикулярен к заданным:

Причем его модуль будет равен площади параллелограмма, построенного на векторах \( \vec{a}\) и \( \vec{b}\).

Данный вектор понадобится нам для вычисления расстояния от точки до прямой. Как же нам считать векторное произведение векторов \( \vec{a}\) и \( \vec{b}\), если их координаты заданы?

На помощь к нам опять приходит определитель третьего порядка.

Однако, прежде чем я перейду к алгоритму вычисления векторного произведения, я вынужден сделать небольшое лирическое отступление.

Данное отступление касается базисных векторов.

Базисными векторами в трехмерном пространстве называются три вектора:

\( \vec{i}\left( 1,0,0 \right),~\vec{j}\left( 0,1,0 \right),~\vec{k}\left( 0,0,1 \right)\)Схематично они изображены на рисунке:

Как ты думаешь, а почему они называется базисными? Дело в том, что любой вектор в трехмерном пространстве можно представить через сумму трех базисных векторов:

\( \vec a\left( {x,y,z} \right) = x \cdot \vec i + y \cdot \vec j + z \cdot \vec k.\)Или на картинке:

Справедливость этой формулы очевидна, ведь:

Скалярное произведение векторов

В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.

Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.

Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:

Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов аа; у_а> и bb; y_b> можно было рассчитать так:

Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.

Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).

Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:

Задание. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁ ребра имеют длину:

Рассчитайте угол между векторами DB₁ и BC₁.

Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB₁ и BC₁:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.

Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.

Система координат

С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.

Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции \( y=ax+b\), например, \( y=2{x}-3\).

Напомню, ты строил ее по точкам. Помнишь?

Ты выбирал произвольное число \( x\), подставлял ее в формулу \( y=2{x}-3\) и вычислял таким образом \( y\).

Например, если \( x=0\), то \( y=2\cdot 0-3=-3\), если же \( x=1\), то \( y=2\cdot 1-3=-1\)и т. д.

Что же ты получал в итоге?

А получал ты точки с координатами: \( A\left( 0,-3 \right)\) и \( B\left( 1,-1 \right)\).

Далее ты рисовал «крестик» (систему координат \( X0Y\)), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции \( y=2{x}-3\).

Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB2 = OA2 + OB2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a|2 + |b|2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a|2 + |b|2 — |a — b|2) /2. Подставив координаты в формулу, получим следующее: a*b = (x12 + y12 + x22 + y22 — (x1-x2)2 + (y1-y2)2) /2 = x1*x2 + y1*y2. Равенство доказано.

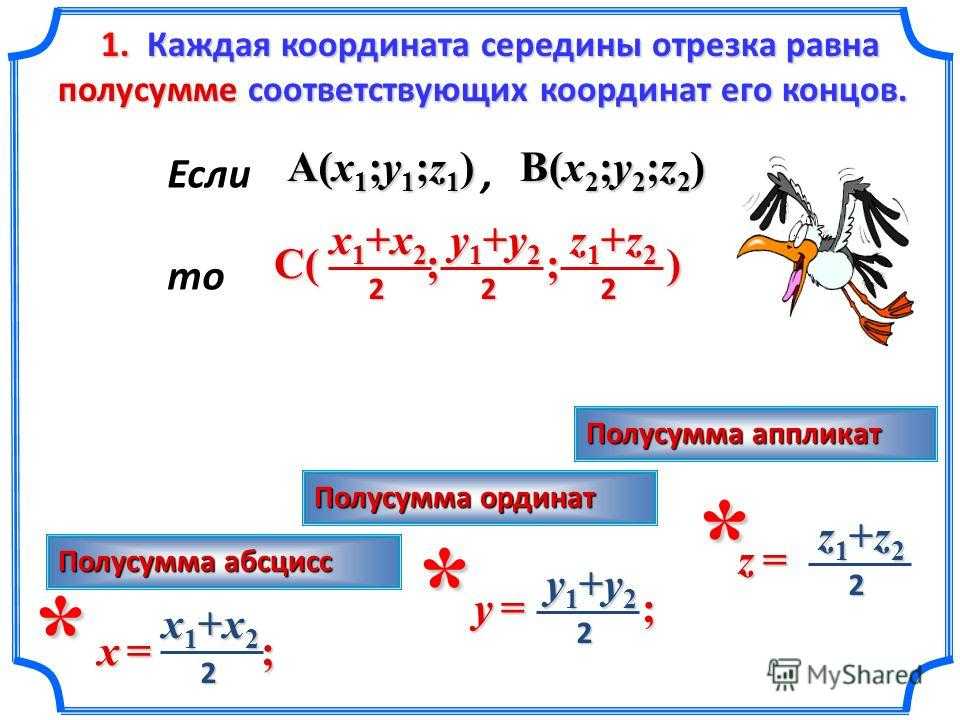
Формулы координат середины отрезка

Даже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы  чудесным образом преображаются в нечто знакомое  и простое:

Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:

В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.

Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины  выражаются формулами:

Пример 7

Параллелограмм  задан координатами своих вершин . Найти точку пересечения его диагоналей.

Решение: Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.

По известному свойству, диагонали параллелограмма своей точкой пересечения  делятся пополам, поэтому задачу можно решить двумя способами.

Способ первый: Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :

В результате:

Способ второй: Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :

Таким образом:

Ответ:

Пространственный отрезок для самостоятельного решения:

Пример 8

Даны точки . Найти середину  отрезка .

Вычисления не самые простые получились, числа с ходу придумал. Решение в конце урока.

Как видите, задача деления отрезка пополам настолько прозрачна, что доступна и пятикласснику. На практике середину отрезка чаще всего находят, чтобы составить уравнение медианы треугольника. Но это уже тема другой статьи

Не вижу смысла открывать трёхлитровую банку примеров, поэтому заключительный аккорд урока – случай, когда известна середина отрезка и один из его концов:

Пример 9

Точка  делит отрезок  пополам. Найти точку , если известны точки

Решение: Используем формулы координат середины отрезка:

Нам неизвестны координаты . И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:

Ответ:

Проверка выполняется даже устно: берём концы отрезка  и находим его середину.

Удачного распила!

Решения и ответы:

Пример 2: Решение: а) . Используем формулы деления отрезка в данном отношении: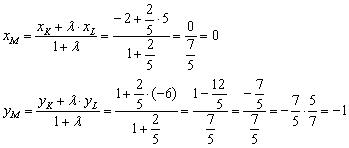Ответб) . Используем формулы деления отрезка в данном отношении: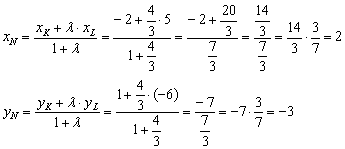Ответ

Пример 4: Решение: Используем формулы деления отрезка в данном отношении:Из условия следует, что .

Примечание: формулировка условия «отрезок  в полтора раза короче отрезка » эквивалентна формулировке «отрезок  в полтора раза длиннее отрезка », именно из этих соображений и составлена пропорция.

По условию , таким образом:Ответ

Пример 6: Решение: Используем формулы деления отрезка в данном отношении:В данной задаче .Таким образом:Ответ

Пример 8:  Решение: Используем формулы координат середины отрезка:Ответ

(Переход на главную страницу)

Расположение на плоскости

Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

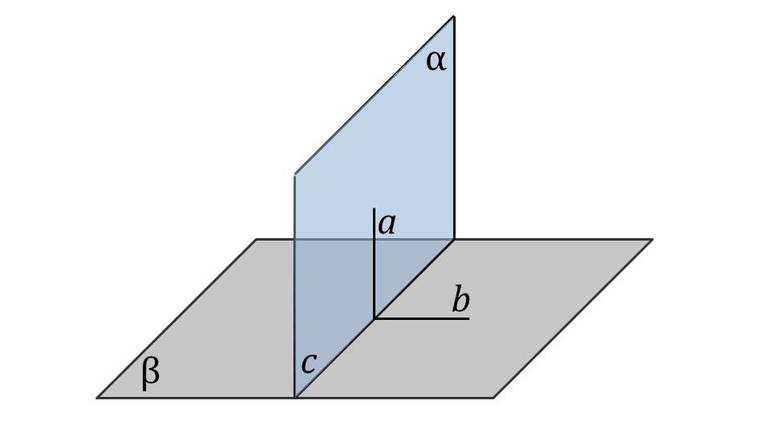
Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма \(ABCFDE\), ребра которой равны 2. Точка \(G\) — середина ребра \(CE\).

Докажите, что прямые \(AD\) и \(BG\) перпендикулярны.
Найдите расстояние между прямыми \(AD\) и \(BG\).

Решение:

Решим задачу полностью методом координат.

Глава 28. Расстояние между двумя точками. Деление отрезка в данном отношении

Расстояние d между двумя точками
(,
,
)
и
(,
,
)
в пространстве определяется формулой

.

Координаты x, y, z
точки М, которая делит отрезок , ограниченный
точками
(,
,
) и
(,
,
), в отношении ,
определяется по формулам

,
,
.

В частности, при имеет координаты
середины данного отрезка:

,
,
.

Даны точки A(1; -2; -3), B(2; -3; 0), C(3; 1;
-9), D(-1; 1; -12). Вычислить расстояние между 1). А и С, 2). B
и D, 3). C и D.

Вычислить
расстояния от начала координат О до точек A(4; -2; -4),
B(-4; 12; 6), C(12; -4; 3), D(12; 16; -15).

Доказать, что
треугольник с вершинами A(3; -1; 2), B(0; -2; 2), C(-3; 2; 1)
равнобедренный.

Доказать, что
треугольник с вершинами A₁(3; -1;
6), A₂(-1; 7; -2), A₃(1; -3; 2) прямоугольный.

Определить, есть ли
тупой угол среди внутренних углов треугольника с
вершинами M₁(4; -1; 4), M₂(0; 7; -4),
M₃(3; 1; -2).

Доказать, что
внутренние углы треугольника M(3; -2; 5), N(-2; 1; -3), P(5; 1;
-1) острые.

На ось абсцисс
найти точку, расстояние от которой до точки А(-3; 4;
равно 12.

На оси ординат
найти точку, равноудаленную отточек А(1; -3; 7) и В(5;
7; -5).

Найти центр C и
радиус R шаровой поверхности, которая проходит
через точку P(4; -1; -1) и касается всех трех
координатных плоскостей.

Даны вершины M₁(3; 2; -5), M₂(1; -4; 3), M₃(-3; 0; 1) треугольника. Найти середины его
сторон.

Даны вершины A(2; -1; 4).
B(3; 2; -6), C(-5; 0; 2) треугольника. Вычислить длину его
медианы, проведенной из вершины А.

Центр масс
однородного стержня находится в точке С(1; -1; 5),
один из его концов есть точка A(-2; -1; 7). Определить
координаты другого конца стержня.

Даны две вершины A(2;
-3; -5), B(-1; 3; 2) параллелограмма ABCD и точка
пересечения его диагоналей E(4; -1; 7). Определить
две другие вершины этого параллелограмма.

Даны три вершины A(3;
-4; 7), B(-5; 3; -2), C(1; 2; -3) параллелограмма ABCD. Найти его
четвертую вершину D, противоположную B.

Даны три вершины A(3;
-1; 2), B(1; 2; -4), C(-1; 1; 2) параллелограмма ABCD. Найти его
четвертую вершину D.

Отрезок прямой,
ограниченный точками A(-1; 8; 3), B(9; -7; -2), разделен
точками C, D, E. F на пять равных частей. Найти
координаты этих точек.

Определить
координаты концов отрезка, который точками C(2; 0;
2), D(5; -2; 0) разделен на три равные части

Даны вершины
треугольника A(1; 1; -1), B(2; -1; 3), C(-4; 7; 5). Вычислить
длину биссектрисы его внутреннего угла при
вершине B.

Даны вершины
треугольника A(1; -1; -3), B(2; 1; -2), C(-5; 2; -6). Вычислить
длину биссектрисы его внутреннего угла при
вершине А.

В вершинах
тетраэдра A(x₁, y₁, z₁),
B(x₂, y₂, z₂), C(x₃, y₃, z₃),
D(x₄, y₄, z₄) сосредоточены
равные массы. Найти координаты центра масс этой
системы.

В вершинах
тетраэдра A₁(x₁, y₁, z₁),
A₂(x_, y₂, z₂), A₃(x₃, y₃,
z₃), A₄(x₄, y₄, z₄) сосредоточены массы m₁, m₂,
m₃, m₄. Найти координаты
центра масс этой системы.

Прямая проходит
через две точки M₁(-1; 6; 6) и M₂(3; -6; -2). Найти
точки ее пересечения с координатными
плоскостями.

Текст издания: Д.В.Клетеник «Сборник задач по аналитической геометрии». М., Наука, Физматлит, 1998Решение задач: 2004-2013, Кирилл Кравченко, http://a-geometry.narod.ru/, http://kirill-kravchenko.narod.ru/

Определение компланарности векторов

Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.

Задание. Определите, компланарны ли вектора

Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.

Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.

Правила нахождения координат середины отрезка, формулы

Середина отрезка на координатной прямой

Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа x_A и x_B, а точка С делит AB пополам. Определите координату x_C, соответствующую С. 

Так как C — это середина AB, то справедливо следующее равенство:

\(\left|AC\right|=\left|CB\right|\)

Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:

\(\left|AC\right|=\left|CB\right|\Leftrightarrow\left|x_C-x_A\right|=\left|x_B-x_C\right|\)

Опустим знак модуля и получим справедливость двух выражений:

\(x_C-x_A=x_B-x_C\)

\(x_C-x_A=-\left(x_B-x_C\right)\)

Исходя из первого равенства, получим формулу нахождения x_C, согласно которой координата точки С равна половине суммы координат A и B:

\(x_C=\frac{x_A+x_B}2\)

Следствием второго равенства будет следующее утверждение: 

\(x_A=x_B\)

Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:

\(x_C=\frac{x_A+x_B}2\)

Середина отрезка на плоскости

В декартовой системе координат Oxy расположены две точки A(x_A,y_A) и B(x_B,y_B), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат x_C и y_C, соответствующих С.

Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат A_x, A_y; B_x, B_y; C_x, C_y — это проекции исходных точек.

По построению прямые AA_x, BB_x, CC_x относительно друг друга находятся параллельно. Прямые AA_y, BB_y, CC_y не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:

\(A_xC_x=C_xB_x\)

\(A_yC_y=C_yB_y\)

Это значит, что C_x и C_y являются серединами отрезков A_xB_x и A_yB_y соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:

\(x_C=\frac{x_A+x_B}2\)

\(y_C=\frac{y_A+y_B}2\)

Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(x_A,y_A) и B(x_B,y_B), вычисляются следующим образом:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2\right)\)

Середина отрезка в пространстве

Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(x_A, y_A, z_A) и B(x_B, y_B, z_B). C(x_C, y_C, z_C) — это центр АВ. Задание заключается в том, чтобы определить x_C, y_C, z_C.

Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — A_x, A_y, A_z; B_x, B_y, B_z;C_x, C_y, C_z — проекции точек A, B, C на них.

Воспользуемся теоремой Фалеса:

\(\left|A_xC_x\right|=\left|C_xB_x\right|\)

\(\left|A_yC_y\right|=\left|C_yB_y\right|\)

\(\left|A_zC_z\right|=\left|C_zB_z\right|\)

Исходя из полученных равенств следует, что C_x, C_y, C_z — делят A_xB_x, A_yB_y, A_zB_z пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(x_A,y_A,z_A) и B(x_B,y_B,z_B) используем формулу:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)