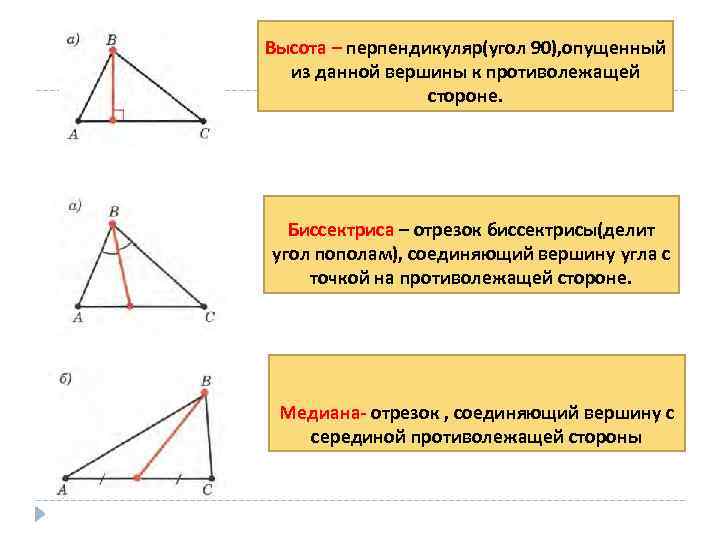
Задачи на пересечение двух фигур
Метод координат помогает находить точки, в которых пересекаются те или иные геометрические фигуры. В большинстве случаев надо просто составить систему из уравнений, задающих эти фигуры, и найти их общее решение. В курсе алгебры мы уже рассматривали как решение простых, в основном линейных систем, так и решение более сложных, нелинейных систем. Рассмотрим несколько задач на эту тему.
Задание. Две прямые заданы уравнениями:
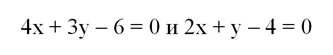
Определите, в какой точке они пересекаются.
Решение. Если точка пересечения прямых существует, то ее координаты являются решением каждого из двух уравнений. Таким, образом, нам надо просто решить систему:

Мы нашли единственное решение системы – это пара чисел (3; – 2). Эта же пара определяет координаты искомой нами точки.
Ответ: (3; – 2).
Задание. Найдите точки пересечения окруж-ти и прямой, если они задаются уравнениями

Решаем квадратное уравнение, используя дискриминант:
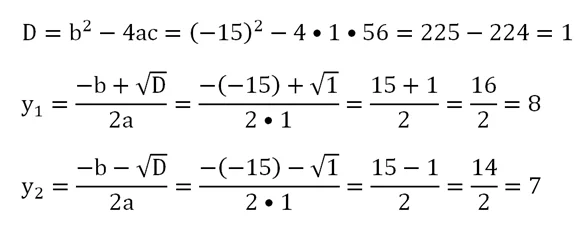
Мы нашли два различных значения у. Это значит, что прямая пересекается с окруж-тью в двух различных точках, а найденные нами числа – их ординаты. Отметим, что возможны случаи, когда корень только один (и тогда у окруж-ти с прямой одна общая точка, то есть они касаются), и когда корней вовсе нет (тогда окруж-ть и прямая не пересекаются). В нашем же примере осталось найти абсциссы точек. Для этого используем уравнение (3):
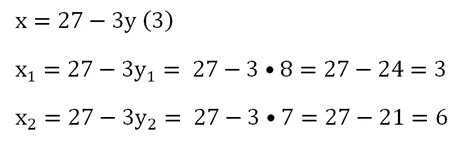
Получили в итоге пары точек (3; ![]() и (6; 7), в которых заданная окруж-ть и прямая пересекаются.
и (6; 7), в которых заданная окруж-ть и прямая пересекаются.
Ответ: (3; ![]() и (6; 7).
и (6; 7).
Задание. Две окруж-ти заданы уравнениями:

Для ее решения сначала раскроем скобки в обоих уравнениях и приведем подобные слагаемые:

Нам удалось выразить у через х. Теперь снова запишем одно из исходных уравнений окруж-ти, но заменим в нем у с помощью только что найденного выражения:

Мы нашли абсциссы точек пересечения окруж-тей, теперь можно вернуться к (1), чтобы найти и ординаты:
Получили точки (5; 2) и (4; 3).
Ответ:(5; 2) и (4; 3).
В конце решим одну задачу чуть более высокого уровня сложности.
Задание. К окруж-ти радиусом 5, чей центр совпадает с началом координат, построена касательная в точке (3; 4). Составьте уравнение этой касательной.
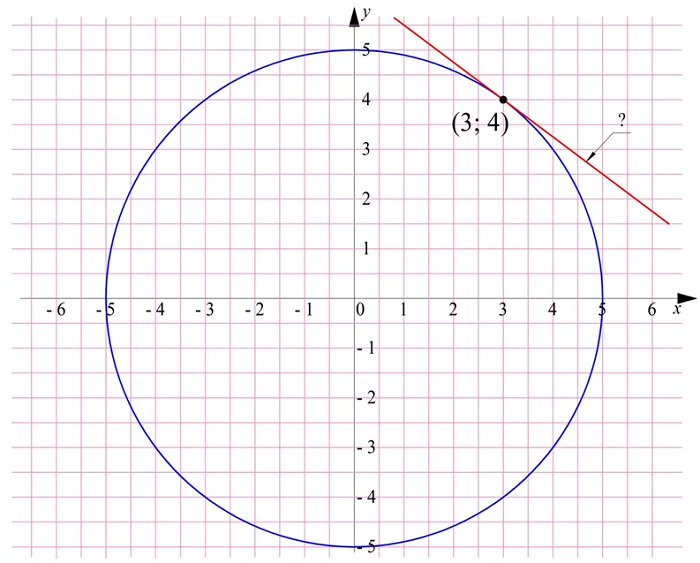
Решение. Сначала составим уравнение окруж-ти. Так как ее центр находится в начале координат, а радиус имеет длину 5, то оно примет вид:

Нам надо найти коэффициенты k и d, а для этого надо составить какие-нибудь уравнения с этими переменными. Нам известно, что касательная проходит через точку (3; 4), а потому эти координаты можно подставить в (2):

Обратите внимание, что мы получили квадратное уравнение относительно переменной х. Если бы нам были известны k и d, то мы смогли бы его решить, и тогда мы определили бы точки пересечения прямой и окруж-ти
В этой задаче k и d нам неизвестны, но мы знаем, что окруж-ть и прямая касаются, то есть имеют ровно одну общую точку. Но тогда и квадратное уравнение (4) должно иметь только одно решение! Это означает, что его дискриминант равен нулю. Сначала выпишем коэффициенты квадратного уравнения, используемые при вычислении дискриминанта:

Теперь у нас есть два уравнения, (3) и (5), которые содержат только переменные k и d. Осталось лишь совместно решить их. Для этого подставим (3) в (5):

В рамках урока мы выяснили, как выглядят уравнения окруж-ти и прямой, а также научились решать несколько типовых заданий, в которых эти уравнения необходимо использовать. Хотя формулы, используемые при этом, могут показаться слишком сложными, главное – просто набить руку в их применении, решая как можно больше задач.
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .
Решение
Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:
4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:
— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Пример 8
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ
Ответ: x = 1 2 + x · λ y = 2 3 — λ .
Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ
Ответ: x = 3 · λ y = — 7 — 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Пример 10
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .
Уравнение прямой с угловым коэффициентом
Всем известный «школьный» вид уравнения прямой называется уравнением прямой с угловым коэффициентом . Например, если прямая задана уравнением , то её угловой коэффициент: . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой: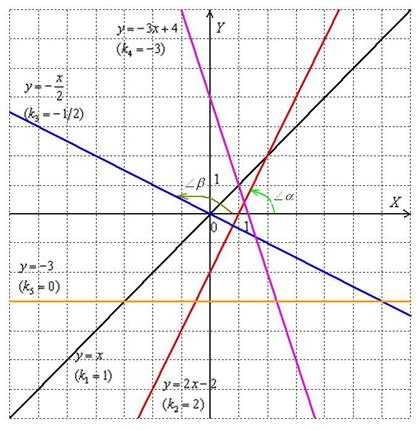
В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси и данной прямой: , причём угол «откручивается» против часовой стрелки.
Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую и её угловой коэффициент . Согласно вышесказанному: (угол «альфа» обозначен зелёной дугой). Для «синей» прямой с угловым коэффициентом справедливо равенство (угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Как говорится, тригонометрическая таблица или микрокалькулятор в руки. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.
При этом возможны следующие случаи:
1) Если угловой коэффициент отрицателен: , то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.
2) Если угловой коэффициент положителен: , то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.
3) Если угловой коэффициент равен нулю: , то уравнение принимает вид , и соответствующая прямая параллельна оси . Пример – «жёлтая» прямая.
4) Для семейства прямых , параллельных оси (на чертеже нет примера, кроме самой оси ), углового коэффициента не существует (тангенс 90 градусов не определён).
Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.
Например, рассмотрим две прямые . Здесь , поэтому прямая имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
В свою очередь, прямая более крутА, чем прямые .
Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой.
Для прямых справедливо неравенство , таким образом, прямая более полога. Детская горка, чтобы не насадить себе синяков и шишек.
Зачем это нужно?
Продлить ваши мучения Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – если на чертеже получилось «явно что-то не то». Желательно, чтобы вам сразу было понятно, что, например, прямая весьма крутА и идёт снизу вверх, а прямая – очень полога, близко прижата к оси и идёт сверху вниз.
В геометрических задачах часто фигурируют несколько прямых, поэтому их удобно как-нибудь обозначать.
Обозначения: прямые обозначаются маленькими латинскими буквами: . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через .
Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: и т.д. Обозначение совершенно очевидно подразумевает, что точки принадлежат прямой .
Пора немного размяться:
Как составить уравнение прямой с угловым коэффициентом?
Если известна точка , принадлежащая некоторой прямой, и угловой коэффициент этой прямой, то уравнение данной прямой выражается формулой:
Пример 1
Составить уравнение прямой с угловым коэффициентом , если известно, что точка принадлежит данной прямой.
Решение: Уравнение прямой составим по формуле . В данном случае:
Ответ:
Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение и убеждаемся, что наш угловой коэффициент на своём месте. Во-вторых, координаты точки должны удовлетворять данному уравнению. Подставим их в уравнение:
Получено верное равенство, значит, точка удовлетворяет полученному уравнению.
Вывод: уравнение найдено правильно.
Более хитрый пример для самостоятельного решения:
Пример 2
Составить уравнение прямой, если известно, что её угол наклона к положительному направлению оси составляет , и точка принадлежит данной прямой.
Если возникли затруднения, перечитайте теоретический материал. Точнее больше практический, многие доказательства я пропускаю.
Прозвенел последний звонок, отгремел выпускной бал, и за воротами родной школы нас поджидает, собственно, аналитическая геометрия. Шутки закончились…. А может быть только начинаются =)
Угол между двумя прямыми
Пусть две неперпендикулярные прямые представляются уравнениями
$$y= a_1 x+ b_1 \\
y= a_2 x+ b_2$$
Тогда угол между двумя прямыми найдется по формуле
$$tg(θ)=\frac{a_2-a_1}{1+ a_1 \cdot a_2}$$
Условие параллельности двух прямых
Две прямые параллельны (или совпадают), если равны их угловые коэффициенты.
Теорема. Прямые $y = k_1 x + b_1$ и $y = k_2 x + b_2$ параллельны тогда и только тогда, когда $k_1 = k_2$ и $b_1 \ne b_2$.
Задача
Проверить, выполняется ли условие параллельности прямых
$2x-3y+1=0$ и $4x-6y-5=0$.
Задача
Составить уравнение прямой линии, проходящей через точку $(1;2)$ параллельно прямой $2x-3y+1=0$.
Условие перпендикулярности двух прямых
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1:
$$k_1 \cdot k_2=-1$$
Задача
При каком значении $k$ уравнение $y=kx+1$ определяет прямую, перпендикулярную к прямой $y=2x-1$?
Задача
Составить уравнение прямой линии, проходящей через точку $(-1;1)$ перпендикулярно к прямой $3x-y+2=0$.
| угловые коэффициенты | прямые |
|---|---|
| Если угловые коэффициенты двух линейных функций равны, то прямые, являющиеся их графиками, параллельны | Параллельные прямые имеют одинаковый наклон. |
| Если угловые коэффициенты двух линейных функций не равны, то прямые, являющиеся их графиками, пересекаются | Если прямые пересекаются, то их наклоны не равны |
| Если произведение угловых коэффициентов равно (-1), то прямые, являющиеся их графиками, перпендикулярны. | Если прямые перпендикулярны, то произведение их наклонов всегда = -1. |
| — | Если прямая параллельна оси ординат, то формула не применима (возникает деление на 0), и для таких прямых угловой коэффициент не определён. |
Параметрические уравнения прямой и плоскости.
Прямая линия (на плоскости или в пространстве) полностью определена, если на ней задана точка \(M_{0}\) и задан ненулевой вектор \(\boldsymbol{a}\), параллельный этой прямой. Разумеется, и точку, и вектор можно выбрать по-разному, но мы будем считать, что они как-то выбраны, и называть их начальной точкой и направляющим вектором. Аналогично, плоскость задается точкой и двумя неколлинеарными векторами, ей параллельными, — начальной точкой и направляющими векторами плоскости.
Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.
Пусть дана прямая. Обозначим через \(\boldsymbol{r}_{0}\) и \(\boldsymbol{a}\) соответственно радиус-вектор ее начальной точки \(M_{0}\) и направляющий вектор. Рассмотрим некоторую точку \(M\) с радиус-вектором \(\boldsymbol{r}\) (рис. 6.1).
Рис. 6.1
Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t\boldsymbol{a}.\label{ref3}
$$
Наоборот, какое бы число мы ни подставили в формулу \eqref{ref3} в качестве \(t\), вектор \(\boldsymbol{r}\) в этой формуле определит некоторую точку на прямой.
Уравнение \eqref{ref3} называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.
Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.
Рассмотрим прямую в пространстве. Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\), соответственно, а вектор \(\boldsymbol{a}\) имеет компоненты \((a_{1}, a_{2}, a_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref3}, мы получим
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t,\ z-z_{0} = a_{3}t.\label{ref4}
$$
Для прямой на плоскости мы получаем, аналогично,
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t.\label{ref5}
$$
Уравнения \eqref{ref4} или \eqref{ref5} называются параметрическими уравнениями прямой.
Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol{p}\) и \(\boldsymbol{q}\) ее направляющие векторы, а через \(\boldsymbol{r}_{0}\) — радиус-вектор ее начальной точки \(M_{0}\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol{r}\) — произвольная точка пространства (рис. 6.2).
Рис. 6.2
Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol{p}\) и \(\boldsymbol{q}\) не коллинеарны, в этом и только этом случае \(\boldsymbol{r}-\boldsymbol{r}_{0}\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_{1}\) и \(t_{2}\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t_{1}\boldsymbol{p}+t_{2}\boldsymbol{q}.\label{ref6}
$$
Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_{1}\) и \(t_{2}\). Наоборот, какие бы числа мы ни подставили как значения \(t_{1}\) и \(t_{2}\), уравнение \eqref{ref6} определит некоторую точку плоскости.
Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\) соответственно, а векторы \(\boldsymbol{p}\) и \(\boldsymbol{q}\) имеют компоненты \((p_{1}, p_{2}, p_{3})\) и \((q_{1}, q_{2}, q_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref6}, мы получим параметрические уравнения плоскости
$$
x-x_{0} = t_{1}p_{1}+t_{2}q_{1},\ y-y_{0} = t_{1}p_{2}+t_{2}q_{2},\ z-z_{0} = t_{1}p_{3}+t_{2}q_{3}.\label{ref7}
$$
Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.
Нормальное уравнение прямой
Если уравнение прямой на плоскости Ах + Ву + С = 0 умножить на число , которое называется нормирующем множителем , то получим
xcosφ + ysinφ — p = 0 –
нормальное уравнение. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ — угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример 5. Дано 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой линии.
уравнение прямой в отрезках:
уравнение прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
; cos φ = 12/13; sin φ= -5/13; p = 5.
Следует отметить, что не каждую прямую можно представить в отрезках, например, параллельные осям или проходящие через начало координат.
Пример 6. Прямая отсекает на координатных осях равные положительные отрезки. Найти её, если площадь треугольника, образованного этими отрезками равна 8 см 2 .
Решение.Искомое уравнение имеет вид: , ab /2 = 8; ab=16; a=4, a=-4. a = -4 < 0 не подходит по условию задачи. Итого: или х + у – 4 = 0.
Пример 7. Какая прямая проходит через точку А(-2, -3) и начало координат.
Решение. Имеем: , где х 1 = у 1 = 0; x2 = -2; y2 = -3.
График линейной функции
При k > 0 линейная функция (1) на всей числовой прямой, а её (прямая линия) имеет вид, изображенный на рис. 1, 2 и 3.
| k > 0 | ||||||
|
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её представляет собой прямую линию, параллельную , и изображен на рис. 4, 5 и 6.
| k = 0 | ||||||
|
При k < 0 линейная функция (1) на всей числовой прямой, а её (прямая линия) имеет вид, изображенный на рис. 7, 8 и 9.
| k < 0 | ||||||
|
Прямые линии
y = kx + b1 и y = kx + b2 ,
имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны.
Прямые линии
y = k1x + b1 и y = k2x + b2 ,
имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.
Прямые линии
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
| y = kx | (2) |
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
|
Прямая (1) пересекает ось Oy в точке, которой (рис. 11) равна b .
При прямая (1) пересекает ось Ox в точке, которой (рис. 12) вычисляется по формуле
Неполное общее уравнение прямой.
Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным.
Рассмотрим все возможные варианты неполного общего уравнения прямой.
При общее уравнение прямой примет вид By+C=0. Это неполное общее уравнение прямой определяет в прямоугольной системе координат Oxy прямую параллельную оси Ох, так как при любых действительных значениях переменной х переменная y принимает одно и то же значение . Другими словами, общее уравнение прямой при определяет геометрическое место точек , ординаты которых равны одному и тому же числу .
При общее уравнение прямой примет вид y=0. Это общее неполное уравнение прямой определяет ось абсцисс Ox.
Аналогично, при имеем неполное общее уравнение прямой вида Ax+C=0. Это уравнение прямой параллельной оси ординат.
При имеем неполное общее уравнение прямой вида x=0 — уравнение координатной прямой Oy.
Если , то общее уравнение прямой примет вид . Это неполное общее уравнение прямой задает прямую, проходящую через начало координат. Действительно, пара чисел удовлетворяет равенству , так как .
Ниже приведена графическая иллюстрация всех видов общего неполного уравнения прямой.
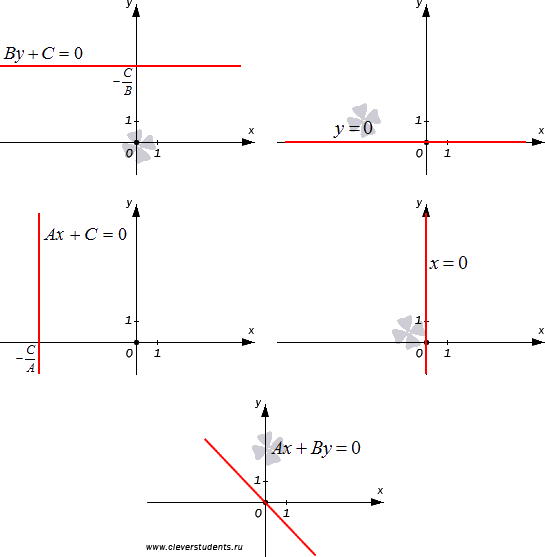
Рассмотрим решения нескольких примеров, связанных с общим неполным уравнением прямой.
Пример.
Напишите общее уравнение прямой, параллельной оси ординат и проходящей через точку .
Решение.
Прямую, которая параллельна оси Oy, задает неполное общее уравнение прямой вида Ax+C=0, где . Так как по условию прямая проходит через точку , то координаты этой точки удовлетворяют уравнению прямой Ax+C=0, то есть, справедливо равенство . Из полученного равенства мы можем вычислить С, если придадим А любое ненулевое действительное значение. Пусть , тогда . Теперь подставляем и С=-2 в уравнение Ax+C=0 и получаем искомое уравнение прямой, параллельной оси ординат и проходящей через точку — оно имеет вид .
Ответ:
Пример.
Напишите уравнение прямой, изображенной на чертеже
Решение.
Очевидно, прямая линия, изображенная на рисунке, параллельна оси абсцисс Ox и проходит через точку .
Прямая линия, параллельная оси абсцисс задается общим неполным уравнением прямой вида By+C=0, . Определим значения В и С.
Так как прямая проходит через точку с координатами , то координаты точки удовлетворяют уравнению прямой By+C=0, следовательно, справедливо равенство . Придадим В любое действительное значение, отличное от нуля. Пусть В=1, тогда из равенства имеем С=-3. При В=1 и С=-3 уравнение By+C=0 примет вид y-3=0.
Ответ:
y-3=0












![Уравнение прямой [love soft]](http://mediaex.ru/wp-content/uploads/2/4/9/24935a5bfa8b02af9b927f171e0102c7.jpeg)