Размерность и базис векторного пространства

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k – 1 ( a k – 1 a 1 ) e 1 + ( a k – 1 a k ) e k + . . . + ( a k – 1 a n ) e n = 0

– a k – 1 a m , где m ∈ 1 , 2 , . . . , k – 1 , k + 1 , n

β 1 e 1 + . . . + β k – 1 e k – 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = ( – β 1 ) e 1 + . . . + ( – β k – 1 ) e k – 1 + ( – β k + 1 ) e k + 1 + . . . + ( – β n ) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

e k = γ 1 e 1 + . . . + γ k – 1 e k – 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k – 1 e k – 1 – e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен – 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Связь между базисами.

Пусть в некотором базисе n-мерного векторного пространства заданы две линейно независимые системы векторов
и
то есть, они тоже являются базисами этого пространства.

Если — координаты вектора в базисе , то связь координат и задается системой линейных уравнений (об этом мы говорили в предыдущем пункте):
, которая в матричной форме может быть записана как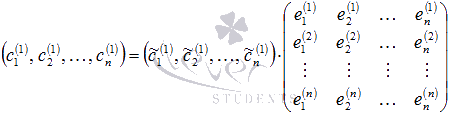

Аналогично для вектора мы можем записать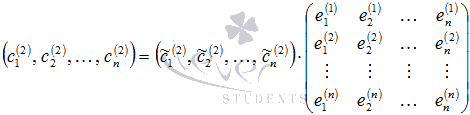

Действуя дальше аналогично, получим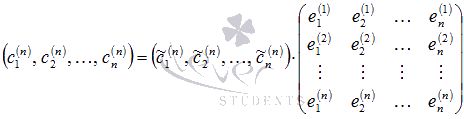

Предыдущие матричные равенства можно объединить в одно, которое по сути задает связь векторов двух различных базисов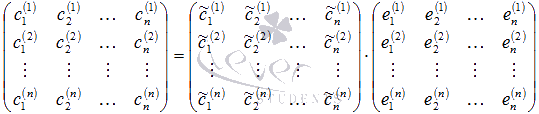

Аналогично мы можем выразить все векторы базиса через базис :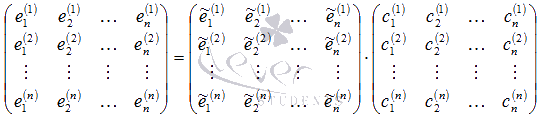

Определение.

Матрицу называют матрицей перехода от базиса к базису ,
а матрицу — матрицей перехода от базиса к базису .

Из двух последних равенств видно, что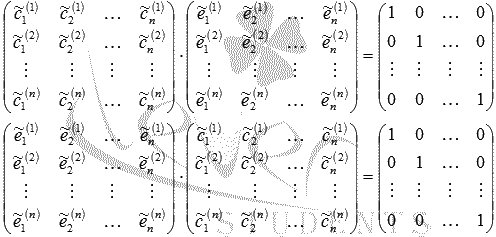
следовательно, матрицы перехода являются взаимно обратными.

Разберем пример.

Пример.

Найдите матрицу перехода от базиса к базису , а также укажите связь координат произвольного вектора x в этих базисах.

Решение.

Пусть T – матрица перехода от базиса к базису , тогда справедливо равенство
Умножив обе части этого равенства справа на
получим
Найдем матрицу перехода, при этом не будем подробно останавливаться на нахождении обратной матрицы и умножении матриц (смотрите при необходимости статьи нахождение обратной матрицы и операции над матрицами):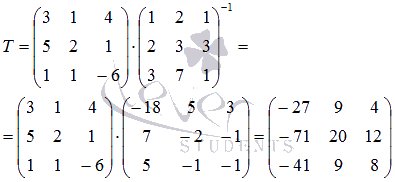

Осталось выяснить связь координат вектора x в заданных базисах.

Пусть в базисе вектор x имеет координаты , тогда
а в базисе вектор x имеет координаты , тогда
Так как левые части последних двух равенств одинаковы, то мы можем приравнять правые части: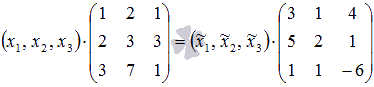
Если умножить обе части справа на
то получим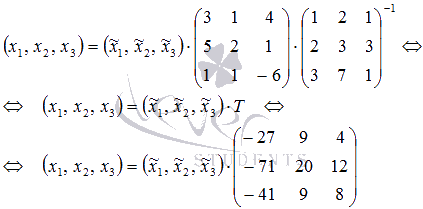
С другой стороны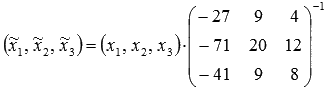
(найдите обратную матрицу самостоятельно).
Два последних равенства дают нам искомую связь координат вектора x в базисах и .

Ответ:

матрица перехода от базиса к базису имеет вид;
координаты вектора x в базисах и связаны соотношениями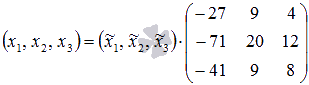
или.

Мы рассмотрели понятия размерности и базиса векторного пространства, научились раскладывать вектор по базису и обнаружили связь между разными базисами n-мерного пространства векторов через матрицу перехода.

Некогда разбираться?

Сайт о разделе высшей математики — линейной алгебре

п.5. Вычисление ранга матрицы и нахождение базиса линейной оболочки ее системы строк (столбцов).

Для вычисления ранга матрицы часто применяют метод Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса основан на элементарных преобразованиях строк матрицы, которые, как мы уже знаем, не изменяют ранга системы строк, а значит не изменяют и ранга матрицы.

Таким образом, ранг данной матрицы равен рангу получившейся после преобразований ступенчатой матрицы. В свою очередь, ранг ступенчатой матрицы легко вычисляется, так как легко увидеть ее максимальный ненулевой минор и его порядок.

Пример. Вычислить ранг матрицы и найти базис и размерность линейной оболочки натянутой на ее столбцы.

1-й шаг: умножим первую строку на 2 и прибавим ко второй строке:

;

2-й шаг: прибавим к третьей строке первую, умноженную на (–3):

;

3-й шаг: прибавим ко второй строке 3-ю, умноженную на (–1):

;

4-й шаг: умножаем вторую строку на (–3) и прибавляем к третьей строке:

Ранг последней матрицы равен 3, так как в первых трех столбцах стоит ненулевой минор 3-го порядка

, а миноров 4-го порядка не существует.

Приведенные преобразования не изменяют величину определителя, построенного на первых трех столбцах матрицы А, поэтому он отличен от нуля и, следовательно, его столбцы линейно независимые и образуют максимальную линейно независимую подсистему системы столбцов матрицы А. Отсюда можно сделать вывод, что первые три столбца матрицы А образуют базис линейной оболочки натянутой на столбцы матрицы А, т.е. и .

Ответ: , – базис линейной оболочки , .

Определение. Любой ненулевой минор матрицы А максимального порядка называют базисным минором матрицы А.

Из этого определения следует, что порядок базисного минора матрицы А равен рангу матрицы А.

Замечание. Максимальную линейно независимую подсистему системы строк матрицы, которая образует базис линейной оболочки системы строк матрицы, мы будем, для краткости, называть базисными строками матрицы. И то же самое для столбцов.

Из приведенного примера можно сделать вывод, что если, вычисляя ранг матрицы, мы не переставляем строки и столбцы матрицы, то найдя базисный минор матрицы и определив номера строк и столбцов на которых он построен, мы, тем самым, находим номера базисных строк и столбцов исходной матрицы.

Так в примере, базисный минор матрицы А построен на первых трех строках и первых трех столбцах, следовательно именно они и образуют базисы системы строк и столбцов матрицы А.

Линейные действия над векторами аналитическим путём

Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:

Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:

Приведём пример:

Пример 1

Найти сумму векторов и , заданных на плоскости .

Решение:

Согласно правилу 1 у нас получается:

= (6, 3).

Построим эти векторы: .

Рис. 3

Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.

Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:

Пример 2

Дан вектор Найти

Решение:

Согласна правилу 2 у нас получается:

Геометрическое изображение смотрите на рис. 4.

Рис. 4

Два вектора равны, если у них равны соответствующие координаты:

Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.

Понятие размерности векторного пространства и базиса.

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.

Определение.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Определение.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n-мерных векторов.

Покажем, что размерность этого пространства равна n.

Возьмем систему из n единичных векторов вида
Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статью ранг матрицы: определение, методы нахождения). Следовательно, система векторов линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы являются базисом этого пространства.

Из последнего утверждения и определения базиса можно сделать вывод, что любая система n-мерных векторов, число векторов в которой меньше n, не является базисом.

Теперь переставим местами первый и второй вектор системы . Легко показать, что полученная система векторов также является базисом n-мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n. Таким образом, система из n векторов линейно независима и является базисом n-мерного векторного пространства.

Если переставить местами другие векторы системы , то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Рассмотрим несколько примеров.

Пример.

Являются ли векторы базисом трехмерного векторного пространства?

Решение.

Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг: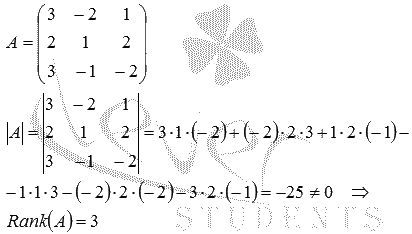
Таким образом, векторы a, b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.

Ответ:

да, являются.

Пример.

Может ли система векторов быть базисом векторного пространства?

Решение.

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема исходной системы векторов является базисом).

Ответ:

нет, не может.

Пример.

Убедитесь, что векторы
могут быть базисом четырехмерного векторного пространства.

Решение.

Составим матрицу, приняв ее строками исходные векторы:
Найдем :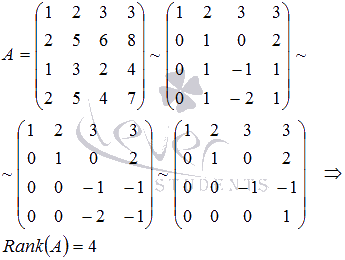
Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Ответ:

исходные векторы действительно являются базисом четырехмерного пространства.

Пример.

Составляют ли векторы базис векторного пространства размерности 4?

Решение.

Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).

Ответ:

нет, не составляет.