Циркуляция вектора напряженности электростатического поля

Разность потенциалов.

Из (6.16) и (6.1) следует, что

Видим, что отношение работы поля по перемещению заряда к
самому этому заряду есть величина, зависящая только от самого поля, т.е. это
скалярная характеристика поля, которую назвали разностью потенциалов.

def: Разностью потенциалов между точками 1 и 2 называется отношение работы, совершаемой
силой электростатического поля по перемещению заряда между этими точками,
к величине этого заряда.

(6.18)

rem: · помним, что изменение потенциала
,
поэтому будем отличать изменение от разности.· Как для любого вида потенциальной энергии, физический
смысл имеет не она сама, а ее разность (или изменение).· Линии электростатического поля не могут быть замкнуты,
иначе вычислив криволинейный интеграл вдоль этой линии (контура) не получим
0. Линии напряженности могут начинаться и заканчиваться на бесконечности
или на зарядах.· Напряженность и потенциал — это два эквивалентных
друг другу способа описания электростатического поля. Напряженность —
это силовая характеристика, а потенциал — энергетическая.· Если среда — не вакуум, то потенциал и напряженность
в e раз меньше, чем в вакууме. Здесь e
— диэлектрическая проницаемость среды.

Потенциальная энергия и потенциал электростатического поля

Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа может быть представлена как разность значений потенциальных энергий, которыми обладает заряд q’ в точках 1 и 2 поля заряда q
Можно показать также, что, так как , .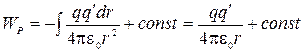
Отсюда для потенциальной энергии заряда в поле заряда q получаем:                              (6)
Значение const в (6) обычно выбирают таким образом, чтобы при удалении заряда q’ на бесконечность () потенциальная энергия обращалась в нуль. При этом условии получается, что                                        (7)
Будем считать q’ пробным зарядом. Тогда потенциальная энергия, которой обладает пробный заряд, зависит не только от его значения , но и от значения q и r, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
Разные пробные заряды , будут обладать в одной и той же точке поля различной энергией , и т.д. Однако отношение   будет для всех зарядов одно и то же. Величина                                          (8)
называется потенциалом поля в данной точке и используется наряду с напряженностью поля , для описания электрических полей.
Как следует из (8) потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Таким образом, для потенциального поля точечного заряда получаем следующее выражение:                                    (9)
Если поле создано системой точечных зарядов q1, q2, …, qn, находящихся на расстояниях соответственно r1, r2,…, rn до точки поля, в которой находится заряд , то работа, совершаемая силами этого поля над зарядом , будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:.
Но каждая из работ равна:
где расстояние от заряда до начального положения    заряда , расстояние от заряда до конечного положения   заряда .
Следовательно:.
Сопоставляя это выражение с соотношением , получаем для потенциальной энергии заряда в поле системы зарядов выражение:,                                   (10)
откуда.                                (11).
Следовательно, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Из соотношения вытекает, что заряд , находящийся в точке поля с потенциалом , обладает потенциальной энергией . Следовательно, работа сил поля над зарядом может быть выражена через разность потенциалов:                     (12)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд из точки с потенциалом удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна или ,
т. е, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля в бесконечность, или работе, которую надо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
За единицу потенциала следует принять потенциал в такой точке поля, для перемещения заряда в которую из бесконечности необходимо совершить работу, равную
1 Джоулю (система единиц “Си”)

Измерение разности потенциалов.

Измерить напряженность — весьма непростая задача. Гораздо
проще измерить разность потенциалов с помощью электрометров (электростатических
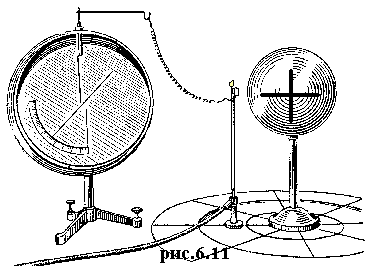
вольтметров), устройство и принцип действия которых понятен из рис.6.9.

Измеряется разность потенциалов между стрелкой и корпусом.
Так можно измерить разность потенциалов между заряженным проводником и Землей
(см. рис.6.10). Электрометр принципиально отличается от электроскопа наличием
металлического корпуса. В случае электроскопа роль корпуса играют окружающие
предметы, поэтому отклонение стрелки зависит от их расположения. Ясно, что электроскопом
измерить разность потенциалов нельзя.

Отметим, что как бы сложна не была форма проводника,
электрометр показывает везде один и тот же потенциал (см. рис.6.10).

При попытках измерить потенциал в диэлектрике (в воздухе)
на пробном шарике возникнет индукционный заряд, а на стрелке электрометра такой
же заряд, но противоположного знака. Возникает сильное искажение первоначального
поля. Электрометр, конечно, покажет потенциал стрелки относительно корпуса,
однако он будет уже другим.

Следовательно, возникает задача убрать индукционный
заряд с пробного шарика. Во-первых, можно подождать довольно долгое время. Тогда
заряды сами стекут с пробного шарика, уравняв его потенциал с потенциалом воздуха
в данной точке пространства. Во-вторых, этот процесс можно ускорить, ионизовав
воздух вокруг шарика. Тогда ионы, разноименные с зарядом шарика, будут переходить
на него до тех пор, пока не нейтрализуют индукционный заряд. Так работает электрический
зонд. Ионизовать воздух можно различными способами, например, с помощью пламени
(пламенный зонд), устройство которого показано на рис.6.11. В-третьих, вместо
пробного шарика можно использовать небольшое ведерко с водой. Если в ведре сделать
дырку, то утекающая вода будет уносить избыточный заряд.

Перемещая зонд в поле заряженного металлического шара,
можно убедиться, что электрометр дает одно и то же показание, если зонд остается
на поверхности сферы, центр которой совпадает с центром шара. Если перемещать
зонд по радиальным прямым, то показания электрометра будут изменяться сильнее
всего.

Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора напряженности электростатического поля. Разность потенциалов. Потенциал

Пусть в некоторой точке находится положительный заряд q1. Вокруг себя он создает электростатическое поле. Найдем работу по перемещению заряда q2 в этом поле из точки 1 в точку 2. Элементарная работа dA на участке dl равна:

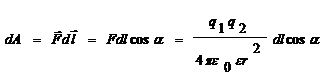.Т.к. ,то .

Работа по перемещению заряда q2 из точки 1 в точку 2 не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Такое поле называют потенциальным, а силы − консервативными.

Теорема о циркуляции вектора напряженности электростатического поля:работа по перемещению заряда по замкнутому контуру потенц. поля равна нулю, т.обр. и циркуляция Е равна нулю: =0; . Интеграл называется циркуляцией вектора напряжённости электростатического поля. Из обращения в нуль циркуляции вектора напряжённости следует, что линии напряжённости электростатического поля не могут быть замкнутыми.

Разность потенциалов —величина, равная совершению работы по перемещению заряда из т.1 в т.2: А12/q=φ1-φ2=U12.

Потенциал − основная энергетическая характеристика электрического поля − есть скалярная величина, равная отношению потенциальной энергии U точечного заряда к величине этого заряда q: . Потенциал поля точечного заряда . С учетом этого работа выразится в виде . Единицей измерения потенциала служит вольт (В). 1 В есть потенциал такой точки поля, в которой заряд 1 Кл обладает потенциальной энергией в 1 Дж. 1 В = 1 Дж/1 Кл. Если перемещать заряд q из произвольной точки за пределы поля, т. е. в бесконечность, где по условию потенциал равен нулю, работа сил электростатического поля , откуда . При q = 1 . Таким образом, потенциал − физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Величину называют разностью потенциалов.

Потенциальная энергия взаимодействия заряженных частиц. Эквипотенциальные поверхности. Применение принципа суперпозиции для потенциалов системы точечных электрических зарядов. Связь потенциала электростатического поля с напряженностью.

Работа при перемещении заряда Qo из одной точки в другую равна: .

Работа сил консервативного поля может быть представлена как убыль потенциальной энергии, т.е. . Сопоставление двух последних формул приводит к выражению для потенциальной энергии заряда Qo в поле заряда Q: .

Значение постоянной выбирается таким образом, чтобы при удалении заряда на бесконечность(r→ ) потенциальная энергия обращалась в нуль. При таком условии .Граф. изображением эл/ст.

поля, кроме линий напряжённости,служат эквипотенциальные поверхности—пов-ти равного потенциала(они перпендикулярны к силовым линиям):

Работа,совершаемая силами эл/ст поля при перемещении эл. Заряда по эквипот-ой пов-ти,равна нулю.

С ростом расстояния потенциал будет уменьшатся. Из и следует:

Связь между напряженностью и разностью потенциалов. Найдем работу по перемещению заряда q в электростатическом поле вдоль оси х на участке dx (из т. 1 в т. 2). По определению dA = Fdx. Согласно (5) F = qE, тогда dA = qEdx. С другой стороны, из (16) следует, что .

Знак «минус» взят из-за того, что работа совершается за счет убыли потенциальной энергии. Приравняем оба выражения для работы , отсюда следует, что . Аналогичная запись верна и для координатных осей у и z.

Для того чтобы подчеркнуть тот факт, что Е изменяется по всем трем координатам пользуются частными производными

Для вектора напряженности имеем или .Знак «минус» указывает на то, что вектор напряженности направлен в сторону убывания потенциала.Градиент показывает скорость изменения к-л физ. Скалярной величины в пространстве.

=1 Н/Кл(1 В/м)

Дата добавления: 2018-05-12; просмотров: 326;

Циркуляция и ротор(математическое отступление).

Как мы видели в пункте 1,
работа электростатического поля оказалась равной криволинейному интегралу, вычисленному
вдоль траектории, по которой движется заряд.

Вообще в математике криволинейный интеграл от любой векторной функции
по кривой (контуру) L означает следующее.
Разделим всю кривую на очень малые элементы
и получим векторы с направлениями,
определяемыми выбором движения, модули которых равны длинам этих участков; для
каждого вычислим скалярное произведение ;
просуммируем
полученные результаты; переходя к пределу бесконечно малых элементов кривой,
получим криволинейный интеграл (или интеграл по контуру).

Пусть теперь в области пространства, в которой определено векторное поле расположена
произвольная замкнутая кривая L (рис.6.3).

def: Циркуляцией вектора
по произвольному замкнутому контуру L называется криволинейный интеграл Г

, (6.7)
где — единичный
вектор, касательный к контуру L, указывающий направление обхода этого
контура.

Фактически интегрируется только касательная составляющая
векторного поля А_l, поэтому помимо (6.7) для обозначения циркуляции
используют ещё следующие эквивалентные формулы:

Будем, кроме того, считать, что на контуре выбрано положительное
направление обхода, то есть направление, при движении, вдоль которого область,
ограниченная контуром, остаётся всегда слева (более точно см. ниже).

Вновь вспомним о гидродинамике. Если мы рассмотрим векторное
поле скоростей текущей
жидкости, и поместим в произвольную точку этой жидкости небольшую турбинку (колёсико
с лопастями) то в зависимости от своей ориентации, турбинка будет вращаться
с большей или меньшей скоростью. Если вычислить циркуляцию вектора скорости
вдоль контура, совпадающего с ободом турбинки, а затем разделить на длину этого
обода, то мы получим (в соответствие с теоремой о среднем) некоторое среднее
значение проекции скорости частиц жидкости на касательную к контуру v_l. Но именно
с такой линейной скоростью и будут вращаться лопасти турбинки. Таким образом,
чем больше циркуляция вектора скорости, тем с большей скоростью будет вращаться
турбинка, помещённая в данную точку жидкости, а это в свою очередь означает,
большую завихрённость жидкости в рассматриваемой точке. (Характерный пример
— вода, вытекающая из ванны.)

Следует отметить, однако, что характеризовать
завихрённость поля непосредственно циркуляцией Г нельзя, поскольку поле может
быть очень неоднородным, и степень его завихрённости будет изменяться от точки
к точке. Желая же определить такую «локальную» завихрённость, мы должны будем
уменьшать размеры контура L, стягивая его в точку. При этом,
очевидно, циркуляция будет стремиться к 0. В связи с этим, для характеристики
степени завихрённости поля вводят понятие плотности циркуляции, определяя её
как предел, к которому стремится отношение циркуляции вектора
по контуру L, к площади
DS,
ограниченной этим контуром, когда данный контур стягивается
к рассматриваемой точке пространства. (При этом, соответственно, DS0):

Вычисляя этот предел, мы будем иметь уже некоторое конечное,
отличное от нуля число. Однако, это значение будет зависеть от ориентации контура L в поле.
Например, как уже говорилось ранее,
от ориентации турбинки в жидкости. Изменяя ориентацию турбинки, мы можем получить
максимальное и минимальное значения Г (соответствующие двум противоположным
ориентациям турбинки, при этом одно из них будет положительным, а другое отрицательным),
а также при некоторой ориентации турбинка вообще перестанет вращаться, что соответствует
Г=0. Данные обстоятельства показывают, что всё многообразие значений плотности
циркуляции векторного поля может быть, вообще говоря, представлено в виде проекции
некоторого вектора, на нормаль к площадке контура L. При этом данный вектор
по абсолютной величине будет равен максимальному значению плотности циркуляции
вектора в рассматриваемой
точке пространства, и направлен в сторону, соответствующую направлению нормали
к контуру L, при которой плотность циркуляции принимает это максимальное значение.

Данный вектор называется ротором или вихрем векторного поля
(от французского
(или английского) слова rotation — вращение, или лат. roto- вращаюсь) и проекция этого
вектора на любое направление в каждой точке пространства определяется
выражением:

(6.10)

Здесь — нормаль
к площадке DS, согласованная с направлением обхода контура L
правилом правого винта (буравчика) — рис.6.4.

Связь между напряженностью электростатического поля и потенциалом

Напряженность электрического поля – величина, численно равная силе, действующей на заряд. Потенциал – величина, численно равная потенциальной энергии заряда. Таким образом, между этими величинами должна существовать связь, аналогичная связи между потенциальной энергией и силой (т.е. ). Работа сил поля над зарядом на отрезке пути может быть представлена как , а убыль потенциальной энергии заряда, которая при этом будет возникать: . Откуда из равенства находим: или ,                                    (21)
где через обозначено произвольно выбранное направление.
Тогда,, , ,                      (22)
Откуда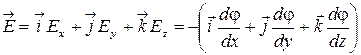,                            (23)
где орты координатных осей, т. е., единичные вектора. Вектор с компонентами , где скалярная функция координат называется градиентом функции и обозначается символом (или , где – оператор набла). Таким образом, градиент потенциала:                               (24)
и из (23) и (24) следует , что                                   (25)

Так как градиент – это вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой, то градиентом потенциала (где r–радиус-вектор) называется вектор, направленный в сторону наиболее быстрого возрастания потенциала, численно равный быстроте его изменения на единицу длины в этом направлении.
Поскольку – векторная величина, то его модуль выражается как:, (26)
подобно тому, как модуль вектора : (27)
Знак “–” (25) указывает на то, что напряженность направлена в сторону убывания потенциала. Формула (25) позволяет по известным значениям найти напряженность поля в каждой точке или решить обратную задачу, т.е., по заданным значения в каждой точке найти разность потенциалов между двумя произвольными точками поля.

Ротор в физике.

Понятно, что если циркуляция напряженности электростатического поля равна 0, то и

(6.15)

Если поле имеет ротор, отличный от нуля, то оно имеет некоторую
завихренность, например, вода, вытекающая из ванны.

Проведем дальнейшие аналогии с гидродинамикой. На
реке скорость течения обычно у берегов меньше, чем на фарватере. Деревянная
щепка может служить “ротор-метром”. Она будет вращаться во всех точках,
кроме строго центральных. Поэтому ротор этого векторного поля скоростей
отличен от нуля.

Чтобы построить электрический “ ротор-метр” — по крайней
мере в воображении — следует положительные пробные заряды прикрепить к
какому-либо центру на изолирующих спицах. Если в поле эта система будет
вращаться, то ротор отличен от нуля. Понятно, что размеры нашего прибора
должны быть достаточно малы.

Соединение с Землей.

Чтобы разрядить какое-либо
тело, мы соединяем его с заземленным предметом, например, с водопроводным
краном, или просто касаемся рукой. При этом мы говорим, что «заряды ушли
с проводника в землю».

Более точно явление заключается
в следующем. Действие электрического поля мы наблюдаем только тогда, когда
есть разность потенциалов между рассматриваемым телом и окружающими предметами.
Если же соединить это тело с землей, то разность потенциалов между этим
телом и окружающими заземленными предметами исчезает, и, следовательно,
исчезает электрическое поле.

Следует заметить, что соединение
именно с землей не играет принципиальной роли. Наблюдалось бы то же самое, если
бы вместо заземленных предметов, например, стен комнаты, был замкнутый проводник
изолированный от земли.

Теорема о циркуляции вектора индукции магнитного поля

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур.

В виде формулы теорема записывается следующим образом:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;M_0\sum_{k=1}^n\;=\;M_0I\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В данном случае I будет означать полный ток.

Теорема используется для того, чтобы облегчить вычисление индукции магнитного поля, созданного совокупностью токов, текущих по проводам. Упрощение достигается с учетом симметрии и конфигурации токов. К примеру, с применением этой теоремы возможен расчет магнитной индукции для проводников с высокой степенью симметрии.

Взглянем на циркуляцию вектора \(\overrightarrow B\). Предположим, что условный замкнутый контур находится в пространстве с магнитным полем, а также предположим направление его обхода. В таком случае, касательная составляющая \(B_l\) вектора \(\overrightarrow B\) определяется на каждом отдельно взятом маленьком участке \(\triangle l \) этого контура. Иными словами определяется проекция вектора \(\overrightarrow B\) на направление касательной к определенному участку контура.

Циркуляцией вектора \(\overrightarrow B\) является сумма произведений \(B_l\) и \(\triangle l\), которая взята по целому контуру L: \(\overrightarrow B = \textstyle\sum_{(L)} B_l \triangle l.\)

Исходя из этого, можно сформулировать следующее: принимая во внимание теорему о циркуляции, циркуляция вектора \(\overrightarrow B\) магнитного поля постоянных токов по каждому из контуров L в любой момент времени рассчитывается как произведение магнитной постоянной \(\mu_0\) на сумму всех токов:

\({\textstyle\sum_{(L)}}\;B_l\;\triangle l\;=\;\mu_0\;{\textstyle\sum_{}}\;l_i\)

Вывод из теоремы: так как циркуляция индукции магнитного поля не равняется нулю, магнитное поле прямолинейного тока не будет являться потенциальным.

\(\oint\limits_L\;(\overrightarrow Bd\overrightarrow l)\;\neq0\) , где \(\overrightarrow B\) обозначает вектор магнитной индукции, а dl является элементом произвольного контура L.

Дивергенция и ротор (Как вы это поняли).

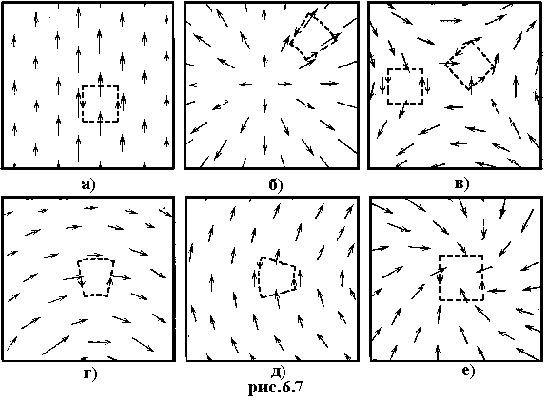
На рис.6.7 представлены различные картины векторного поля. Попробуйте сказать,
где ротор и дивергенция равны 0, а где нет

При этом прежде всего нужно обратить
внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль
каждой из сторон, проекция векторов поля имела одно и тоже значение (причём
для двух сторон в случаях а, б, г, д она равна 0)

Ответ:

a) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой.	б) Явно виден источник поля. Дивергенция не равна нулю. Поле центрально — симметричное. Поэтому ротор равен 0.	в) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю.
г) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0.	д) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю.	е) Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга.

Подводя итог, ещё раз отметим, что ротор характеризует степень
завихрённости векторного поля, его «вращательную составляющую». При этом, однако,
нужно иметь в виду, что данная «вращательная компонента» поля может быть обусловлена
не только искривлением векторных линий (завихрённость «в чистом виде»), как
при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью
поля, когда векторные линии — прямые, как в случае течения воды в реке (рис.6.5),
или в случае примера а).

Циркуляция вектора напряженности электростатического поля

Циркуляция вектора напряженности электростатического поля.

Интеграл …. называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Это есть условие потенциальности поля.

Потенциальная энергия и потенциал электростатического поля.

Из раздела динамики известно, что любое тело (точка), находясь в потенциальном поле, обладает запасом потенциальной энергии Wп, за счет которой силами поля совершается работа. Работа консервативных сил сопровождается убылью потенциальной энергии A=Wп1-Wп2 .

Используя формулу работы силы электростатического поля по перемещению заряда, получим может служить характеристикой поля и называется потенциалом электростатического поля j. Потенциал поля j — скалярная физическая величина, энергетическая характеристика поля, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

Разность потенциалов двух точек поля определяется работой сил поляпри перемещении единичного

потенциал точки поля численно равен работе, совершаемой электрическими силами при перемещении единичного положительного заряда из данной точки поля в бесконечность.

3) электр. Диполь — идеализированная система, служащая для приближённого описания статического поля или распространения электромагнитных волн вдали от источника (особенно — от источника с нулевым суммарно, но пространственно разделенным зарядом).

Полярные – это диэлектрики, в молекулах которых центры распределения положительных и отрицательных зарядов разделены даже в отсутсвие поле, т.е. молекула является диполем. Поляризация: во внешнемэлектр. Поле молекулы ориентируются вдоль векора напряженности внешнего поля Ео( при включении поля молекулы поворачиваются вдоль силовых линий поля)

Неполярные- диэлектрики, в молекулах которых центры распределения положительных и отрицательных зарядов в отсутствие поля совпадают. Поляризация: во внешнем электр.поле в результате деформации молекул возникают диполи, ориентированные вдоль вектора напряженности внешнего поля Ео. (при включении поля молекулы поляризуются)

В электрическом поле диполи подрешеток деформируются: удлиняются, если их оси направлены по полю и укорачиваются, если оси направлены против поля.

Такого рода поляризация называетсяионной. Степень ионной поляризации зависит от свойств диэлектрика и от напряженности поля .

Поляризация- явление возникновения зарядов на поверхности диэлектрика, поле которых частично компенсирует внешнее электр.поле
Величину компенсации описывают с помощью диэлектрической проницаемости среды, которая показывает, во сколько раз эта среда уменьшает электр.поле:
Правила Кирхгофа для разветвленных цепей
Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: .
Второе правило Кирхгофа относится к любому замкнутому контуру, выделенному в разветвленной цепи: алгебраическая сумма произведений токов на сопротивления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре.
Циркуляция вектора напряженности электростатического поля.

Дифференциальная форма теоремы о циркуляции

Предположим, что S — это поверхность, охватываемая контуром L. Правило правого винта будет связывать проложенную к поверхности нормаль и направление обхода контура L. В таком случае определить силу тока, текущего через поверхность S, можно с помощью следующей формулы:

\(I\;=\;\int\limits_S\;\overrightarrow jd\overrightarrow S\)

В этой формуле \(\overrightarrow j\) будет обозначать объемную плотность тока.

Исходя из этого, используем следующее написание формулы:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;\mu_0\int\limits_S\;\overrightarrow jd\overrightarrow S\)

Теперь образуем ротор вектора \(rot\overrightarrow B\), основываясь на теореме Стокса, уточним, что:

\(rot\overrightarrow B\;=\;\begin{vmatrix}i&j&k\\\frac\partial{\partial x}&\frac\partial{\partial y}&\frac\partial{\partial z}\\B_x&B_y&B_z\end{vmatrix} = 0\)

Тогда формула примет вид:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;\int\limits_Srot\overrightarrow Bd\overrightarrow S\)

Теперь можно записать теорему о циркуляции в дифференциальной форме:

Чему равна циркуляция, закон Био–Савара

Циркуляция вектора \( \overrightarrow B\) прямолинейного тока вдоль замкнутого контура, который не охватывает этот проводник, равняется нулю. В случае, когда несколько токов оказываются охваченными контуром, циркуляция вектора \(\overrightarrow B\) равняется их алгебраической сумме:

\(\oint\limits_l\;(\overrightarrow Bd\overrightarrow l)\;=\;\mu_0\sum_i\;l_i\)

Закон Био-Савара определяет вклад \(\triangle\overrightarrow B\) в магнитную индукцию \(\overrightarrow B\) результативного магнитного поля, образуемого маленьким участком \(\triangle l \) проводника с током I.

\(\triangle B\;=\;\frac{\mu_0\;I\;\triangle l\;\sin\left(\alpha\right)}{4\pi r^2}\)

В данном случае r является расстоянием от заданного участка \(\triangle l\) до точки наблюдения, \(\alpha\) обозначает угол между направлением на точку наблюдение и направлением тока на определенном участке, а \(\mu_0\) является магнитной постоянной.

Благодаря закону Био-Савара можно определить магнитные поля током с различными конфигурациями и вычислить магнитное поле в центре кругового витка с током.