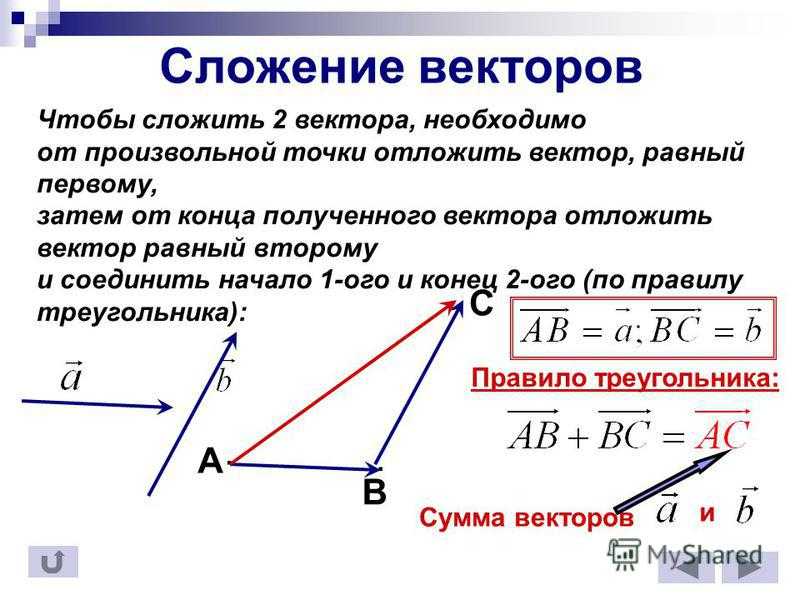
Первый пример с решением
Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.
Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.
Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.
А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.
Ответ. Разность АО и ВО равна 8 см.
Умножение вектора на число
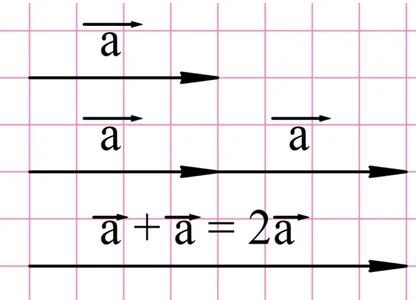
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:
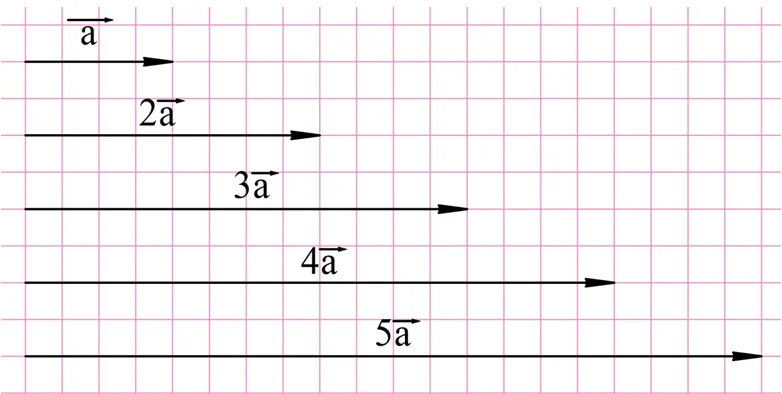
Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:
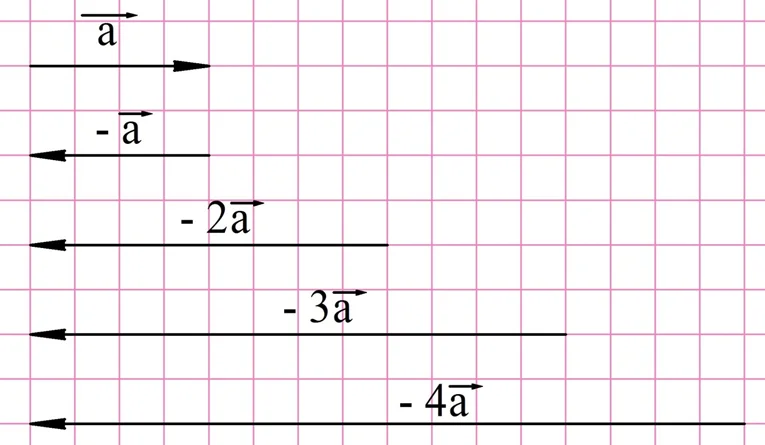
Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:
Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.
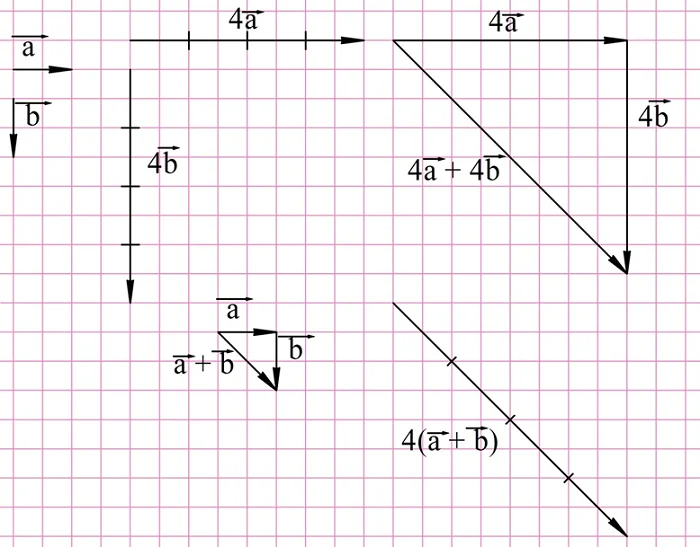
Задание. На рисунке показаны вектора а и b. Найдите вектора
Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:
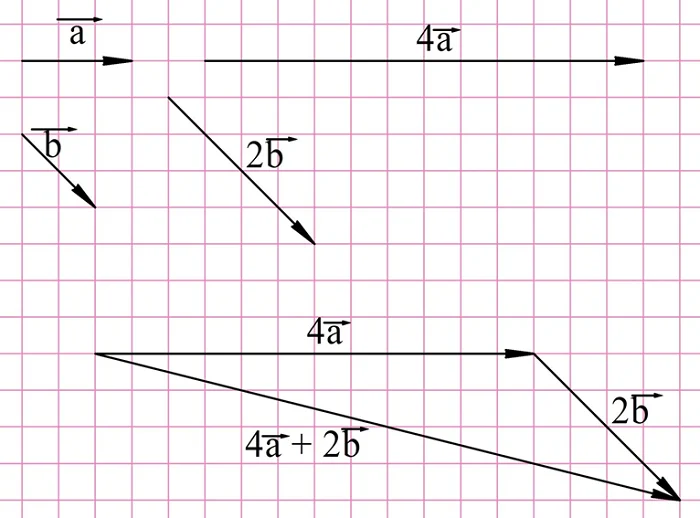
Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:
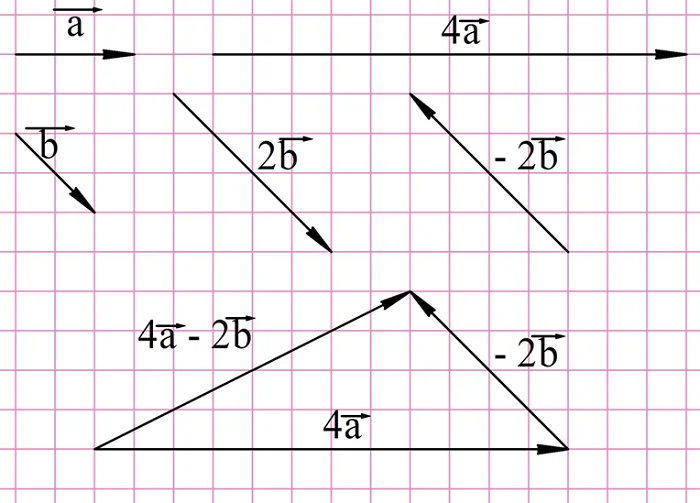
Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:
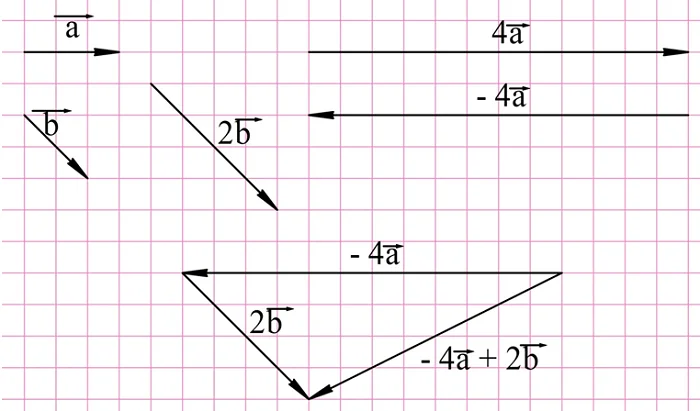
Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:
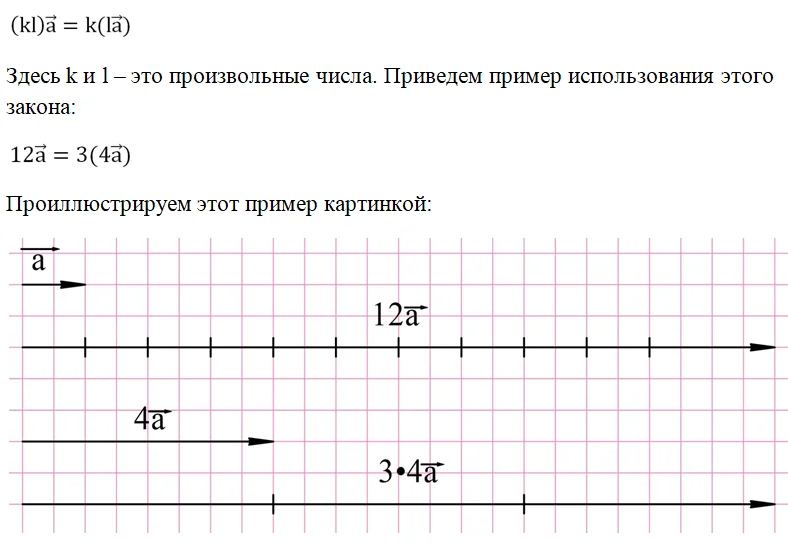
Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.
Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:
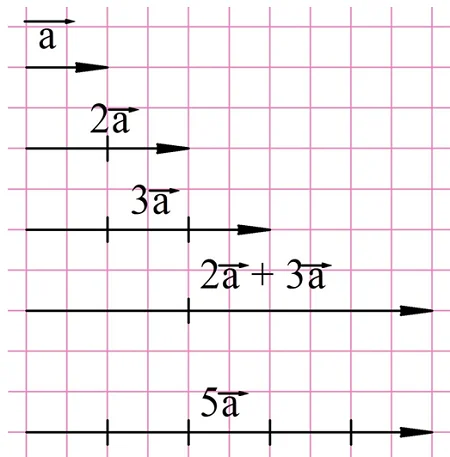
Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:
Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:
Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор

Видно, что выражение значительно упростилось.
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.

Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
- коллинеарными — отрезки лежат на одной линии или ей параллельны;
- соноправленными — замкнутые линии направление которых одинаковое;
- противоположными — вектора направлены в разные стороны;
- ортогональными — перпендикулярными друг другу;
- компланарными — лежащими на одной плоскости или ей параллельные;
- равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.
Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Векторное произведение двух векторов
Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:
Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом
Направление
Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.
Длина
вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.
Начало и конец
Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.
Изменение порядка применения векторов означает изменение знака векторного произведения.
Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A
В отличие от скалярного произведения, векторное произведение некоммутативно.
Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.
В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.
При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).
Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:
Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:
Удобнее всего рассчитать этот определитель, расширив относительно первой строки.
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора и :
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :
Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего перемещения с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
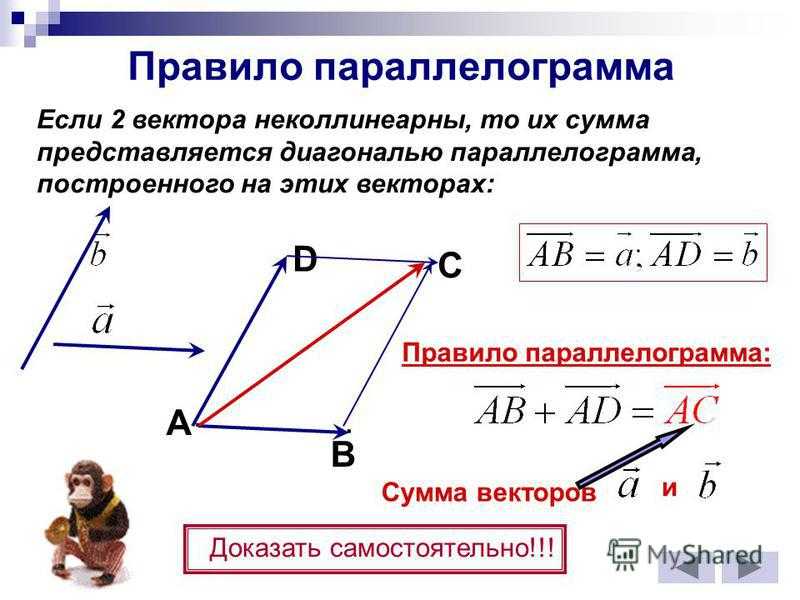
Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация: (векторы сонаправлены) или (векторы направлены противоположно).
Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при .
Правило умножения вектора на число легче понять с помощью рисунка: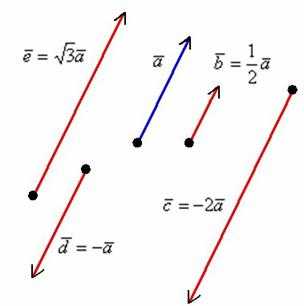
Разбираемся более детально:
1) Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.
2) Длина. Если множитель заключен в пределах или , то длина вектора уменьшается. Так, длина вектора в два раза меньше длины вектора . Если множитель по модулю больше единицы, то длина вектора увеличивается в раз.
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны
Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.
4) Векторы сонаправлены. Векторы и также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
Равенство векторов. Сложение векторов. » Аналитическая геометрия f(x)dx.Ru
п.6. Равенство векторов.
Определение. Два вектора называются равными, если они сонаправленные и имеют равные модули.
Иначе, .
Равные векторы можно обозначать одной буквой (с чертой или со стрелкой): . В этом случае говорят, что вектор отложен от точки А. Если , то говорят, что вектор отложен от точки С. Таким образом, любой вектор можно отложить от любой точки пространства S.
Замечание. На самом деле, понятие равенства векторов расширяет само понятие вектора. Если первоначально под вектором мы понимали упорядоченную пару точек пространства S, т.е. направленный отрезок, то теперь под вектором мы будем понимать множество в с е х направленных отрезков, сонаправленных друг с другом и имеющих одинаковую длину. Если один и тот же вектор отложить от двух различных точек, например, , то направленный отрезок можно совместить с направленным отрезком с помощью параллельного переноса. Часто направленные отрезки и называются представителями одного и того же вектора .
п.7. Сложение векторов.
Пусть – множество всех векторов пространства точек S. Определим на этом множестве операцию сложения векторов.
Определение. Пусть – два произвольных вектора.
Отложим вектор , от какой-нибудь точки А и обозначим его конец буквой В, так что . Вектор отложим от точки В (от конца первого вектора) и обозначим его конец буквой С, так что Тогда вектор называется суммой векторов и и обозначается .
А В
С
рис. 7.
Это правило сложения векторов носит название правило треугольника.
Существует еще одно правило сложения векторов, которое называется правилом параллелограмма и дает точно такой же результат.
Оба вектора и отложим от одной точки А и обозначим через В конец вектора , через D – конец вектора .
Достраиваем до параллелограмма. Через точку D проводим прямую параллельную АВ, через точку В – прямую параллельную AD, точку пересечения построенных прямых обозначим буквой С. Тогда ABCD – параллелограмм. Вектор . См. рис.8:
А В
D С
рис. 8.
Равенство следует из равенства векторов и из определения, т.е. из правила треугольника сложения векторов.
Определение. Вектор, начало и конец которого совпадают, называется нулевым вектором.
Обозначение нулевого вектора: .
Заметим, что модуль нулевого вектора равен нулю:
. Более того, нулевой вектор является нулевым элементом относительно сложения векторов. Этот факт сразу же следует из правила треугольника сложения векторов.
Полагаем также, по определению, что нулевой вектор коллинеарный любому вектору и, более того, сонаправленный с любым вектором и, одновременно, противоположно направлен любому вектору.
Определение. Вектор называется противоположным вектору , если:
1) , т.е. они имеют противоположные направления;
2) – имеют равные модули.
Обозначение. Вектор противоположный вектору обозначается .
Из определения противоположного вектора следует, что если , то . Действительно, и . Из правила сложения векторов (правило треугольника) сразу же следует, что сумма противоположных векторов равна нулевому вектору:
, т.е. .
21 Условие перпендикулярности векторов
Если
ненулевые векторы
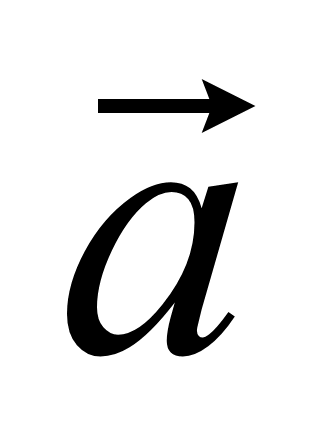
= (x1; y1;
z1) и
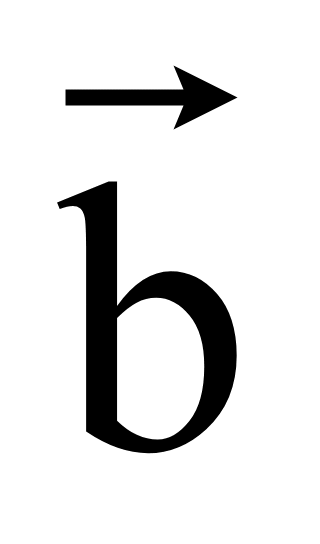
= (x2; y2;
z2) перпендикулярны, то их
скалярное произведение равно нулю
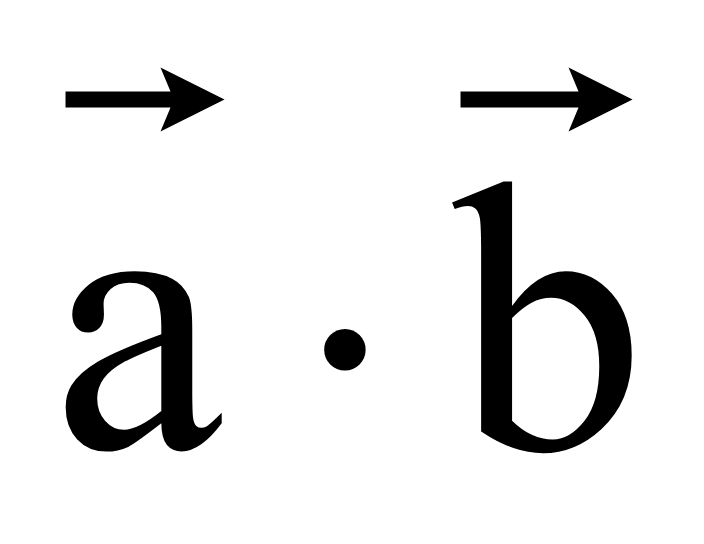 =
=
0,
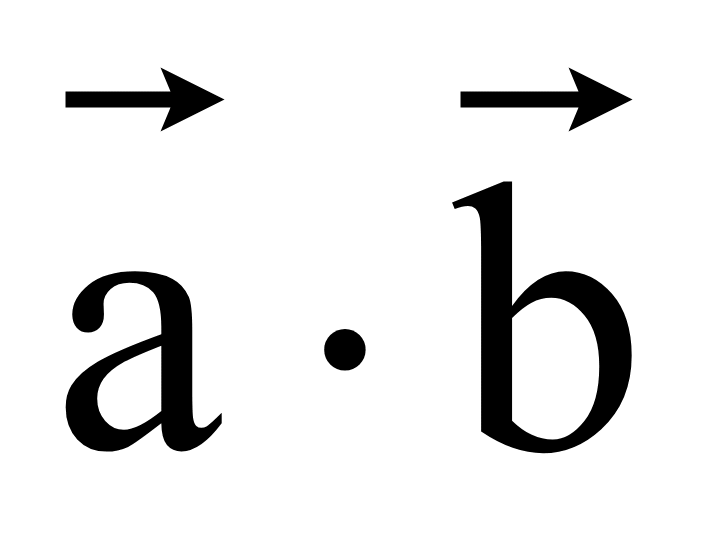 =
=
x1x2
+ y1y2
+ z1z2
= 0.
Если
задан один ненулевой вектор
= (x1; y1;
z1), то координаты
перпендикулярного (нормального) ему ненулевого
вектора
= (x2; y2;
z2) должны удовлетворять
равенству
x1x2
+ y1y2
+ z1z2
= 0.
Таких
векторов
бесконечное множество.
Если
на плоскости задан один ненулевой вектор
= (x1; y1),
то координаты перпендикулярного (нормального) ему вектора
= (x2; y2)
должны удовлетворять равенству
x1x2
+ y1y2
= 0.
Отсюда
можно выразить произведение координат y
y1y2
= — x1x2.
Если
на плоскости задан ненулевой вектор
= (x1; y1),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора
= (x2; y2)
и из условия перпендикулярности векторов
x1x2
+ y1y2
= 0
выразить
вторую координату вектора
.
Например,
если подставить произвольную координату x2,то из равенства
y1y2
= — x1x2
выражается
вторая координата вектора
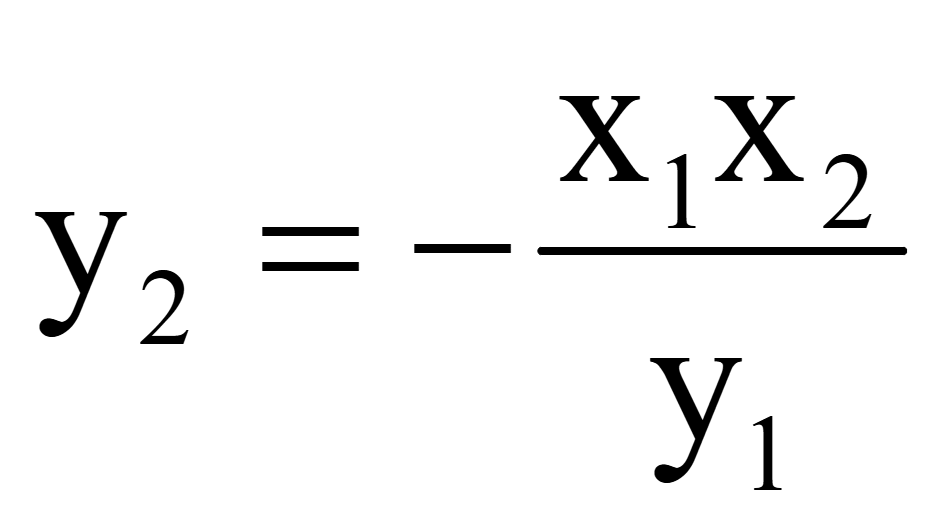
Если
произвольно придать x2 = y1,
то вторая координата вектора
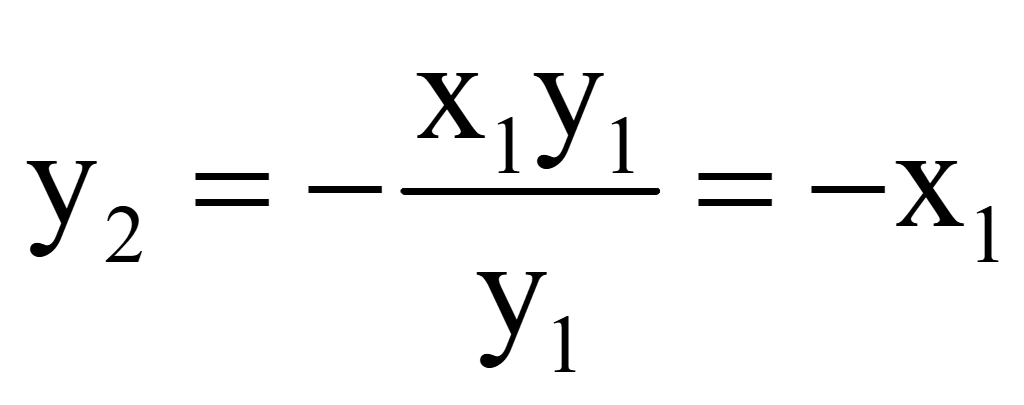
Если
на плоскости задан ненулевой вектор
= (x1; y1),
то перпендикулярный (нормальный) ему вектор
= (y1; -x1).
Если
одна из координат ненулевого вектора
равна нулю, то у перпендикулярного ему ненулевого вектора
такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если
= (; y1),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор
= (x2;
0) лежит на оси Ox.
Определим
второй вектор, перпендикулярный вектору

= (x1; y1),
но противоположный вектору
= (y1; -x1),
то есть вектор —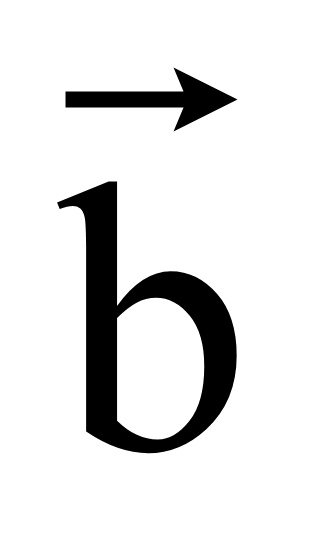
.
Тогда достаточно поменять знаки координат вектора
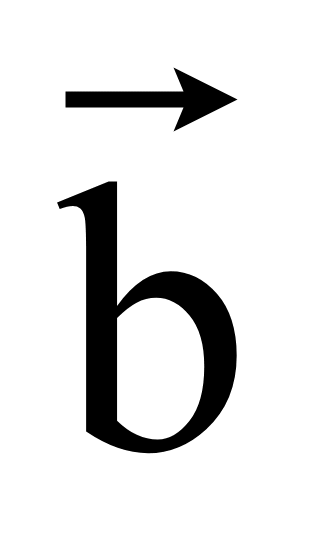
—
= -1·
= (-1·y1;
-1·(-x1))=
(-y1; x1).
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
1
= (y1; -x1),
2
= (-y1; x1).
Для
получения координат ненулевых векторов, перпендикулярных заданному
ненулевому вектору на плоскости, достаточно поменять местами
координаты заданного вектора и поменять знак одной из координат.
Задача.
Задан вектор
= (3; -5). Найти два нормальных вектора с различной ориентацией.
Решение
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
1
= (y1; -x1),
2
= (-y1; x1).
Подставляем
координаты вектора
= (3; -5)
1
= (-5; -3),
2
= (-(-5); 3) = (5; 3).
Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов
x1x2
+ y1y2
= 0
3·(-5)
+ (-5)·(-3) = -15 + 15 = 0
верно!
3·5
+ (-5)·3 = 15 — 15 = 0
верно!
Ответ:
1
= (-5; -3),
2
= (5; 3).
Если
присвоить x2 = 1, подставить
x1
+ y1y2
= 0.
y1y2
= -x1
Получим
координату y2 вектора,
перпендикулярного вектору
= (x1; y1)
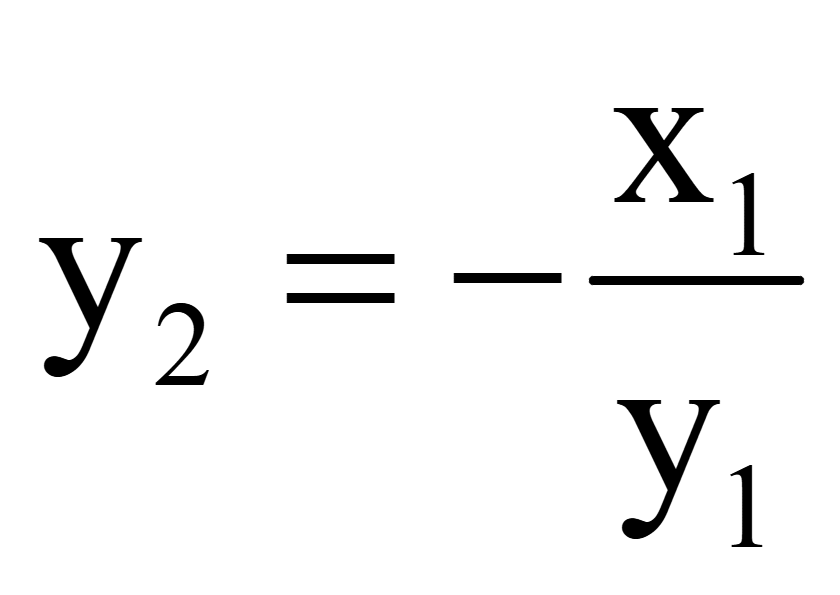
Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору
= (x1; y1)
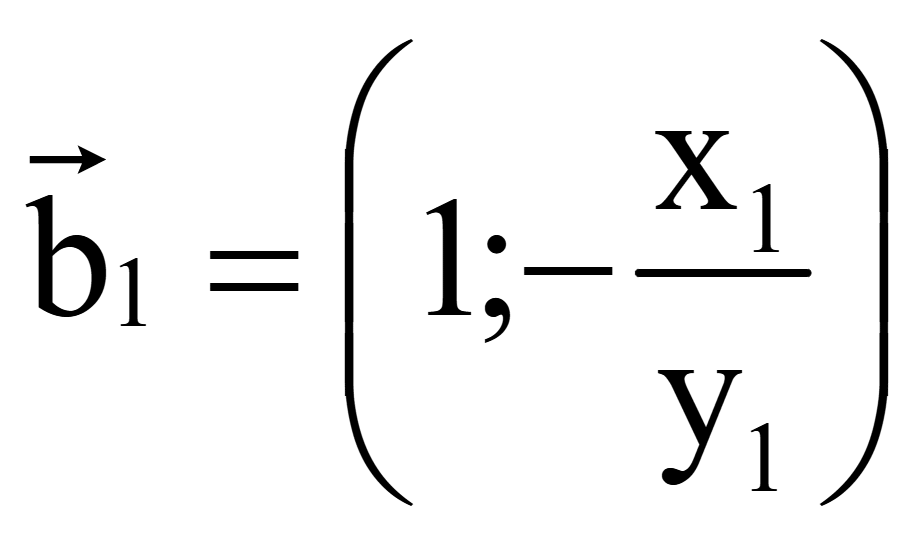
Для
получения второго вектора, перпендикулярного вектору
= (x1; y1),
но противоположно направленного вектору
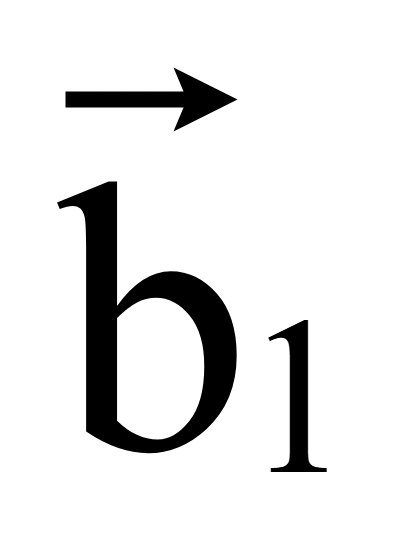
.
Пусть
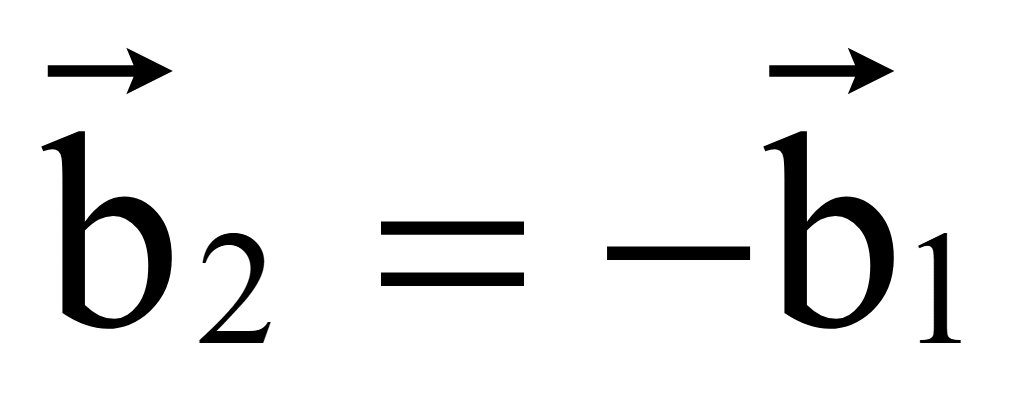
Тогда
достаточно поменять знаки координат вектора
.
Координаты
второго вектора, перпендикулярного на плоскости вектору
= (x1; y1)
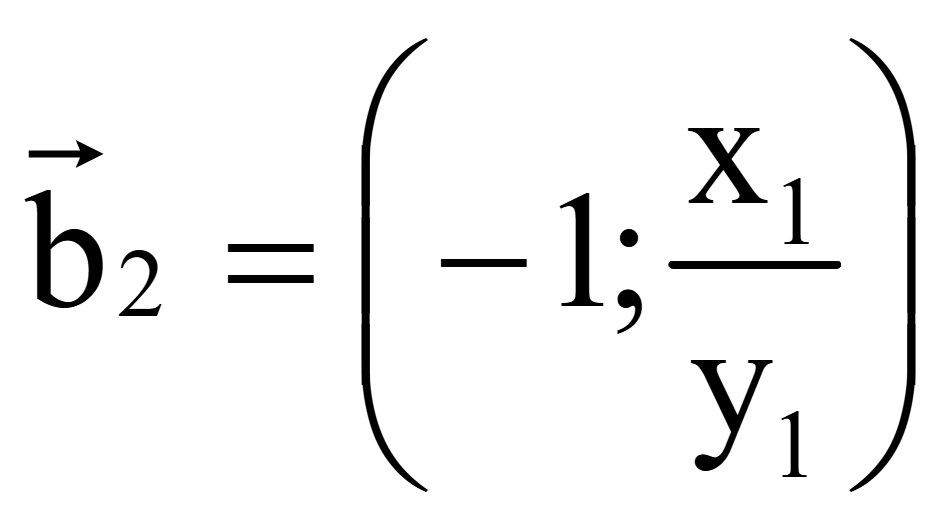
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
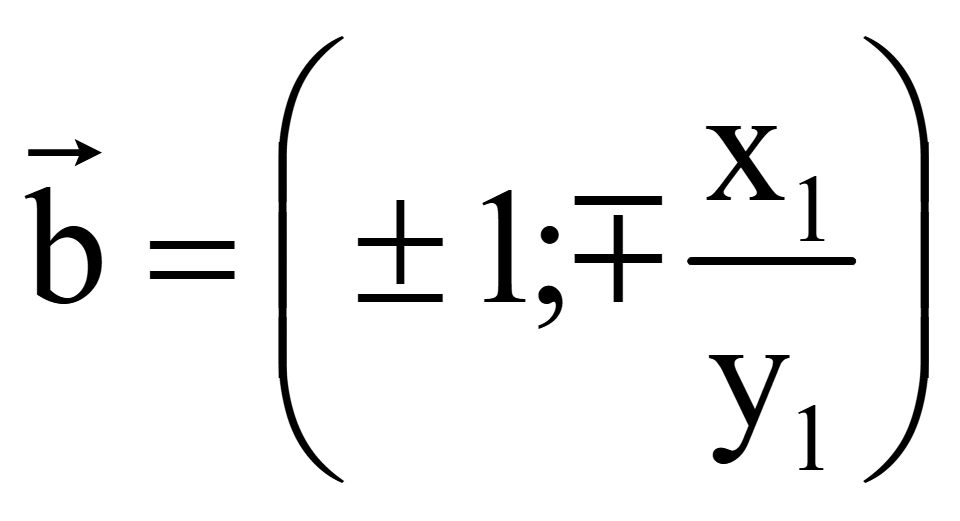
Задача.
Задан вектор
= (3; -5). Найти два нормальных вектора с различной ориентацией.
Решение
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
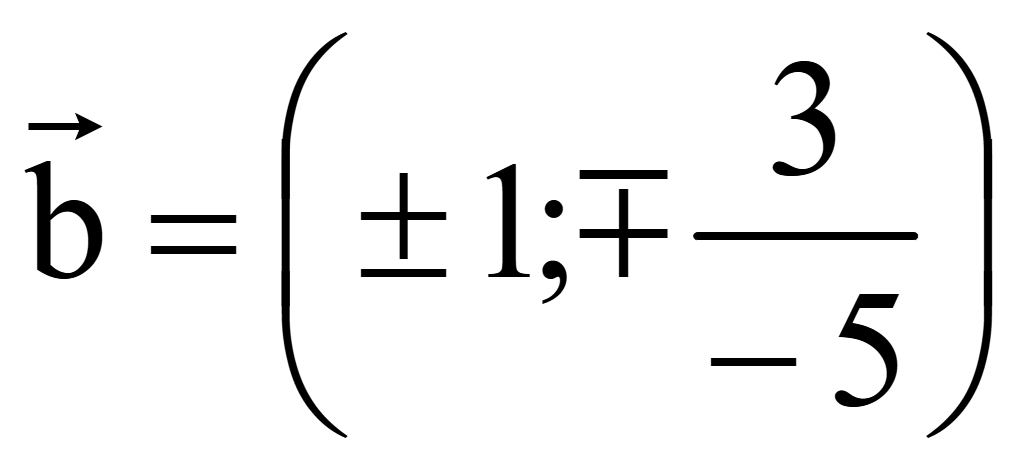
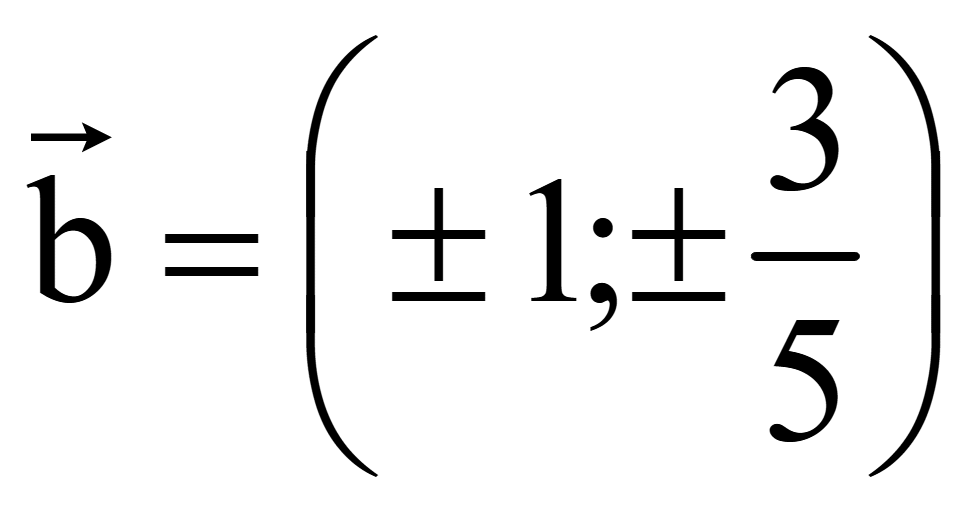
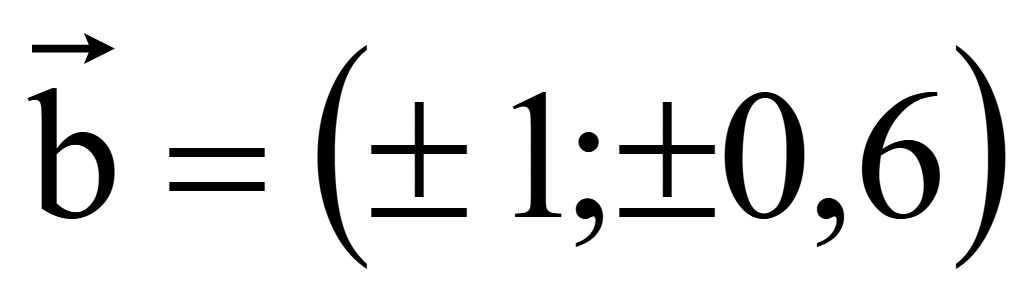
Координаты
одного вектора
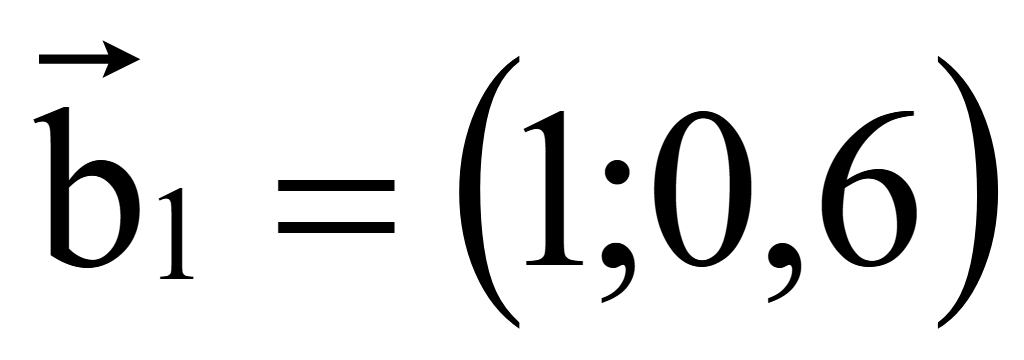
Координаты
второго вектора
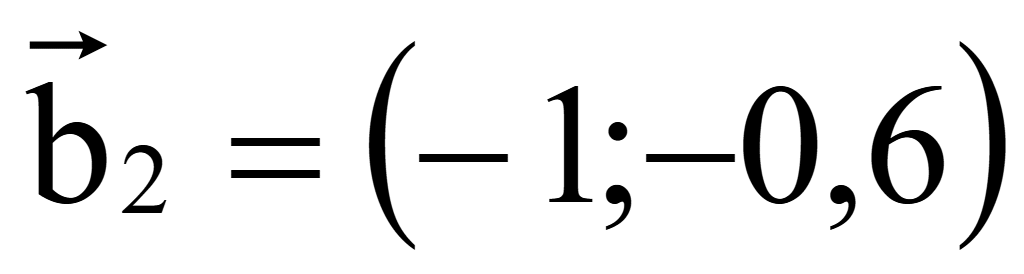
Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов
x1x2
+ y1y2
= 0
3·1
+ (-5)·0,6 = 3 — 3 = 0
верно!
3·(-1)
+ (-5)·(-0,6) = -3 + 3 = 0
верно!
Ответ:
и
.
Если
присвоить x2 = — x1,
подставить
x1(-x1)
+ y1y2
= 0.
-x12
+ y1y2
= 0.
y1y2
= x12
Получим
координату вектора, перпендикулярного вектору
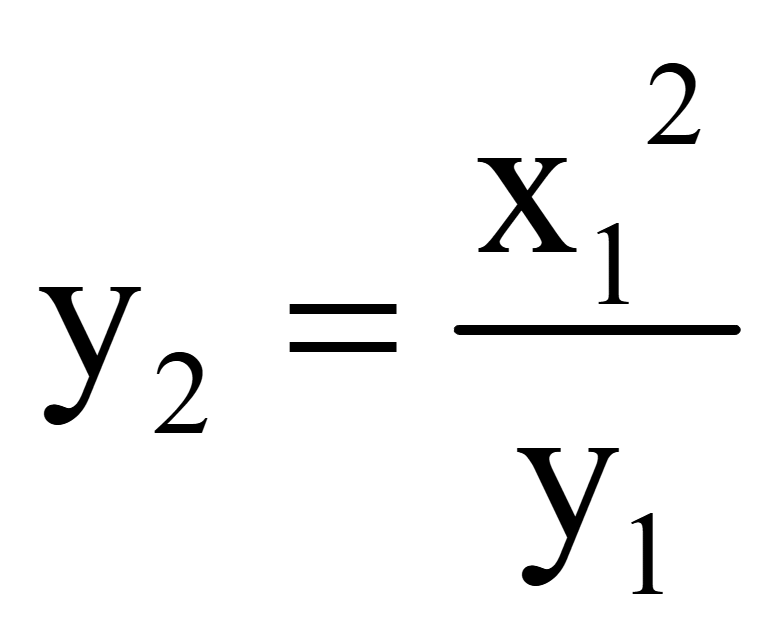
Если
присвоить x2 = x1,
подставить
x1x1
+ y1y2
= 0.
x12
+ y1y2
= 0.
y1y2
= -x12
Получим
координату y второго вектора,
перпендикулярного вектору
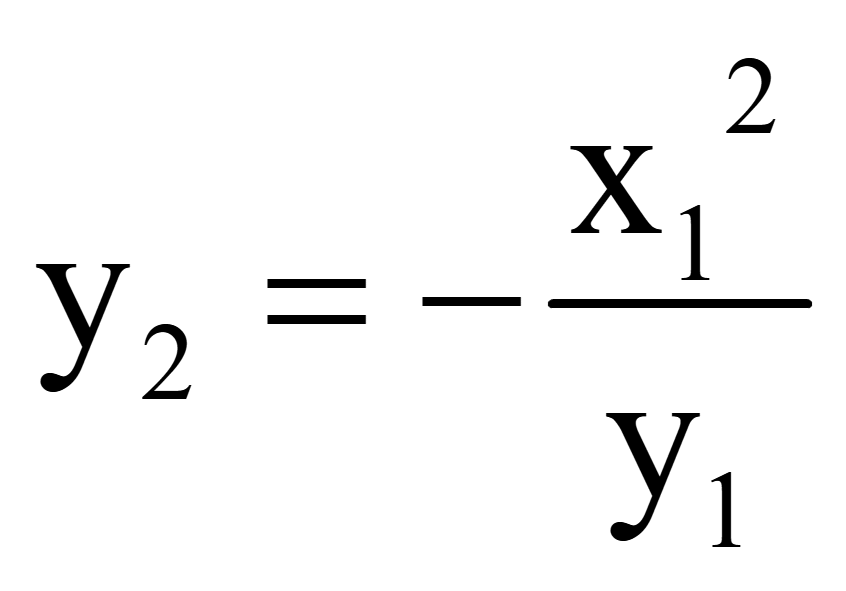
Координаты
одного вектора, перпендикулярного на плоскости вектору
= (x1; y1)
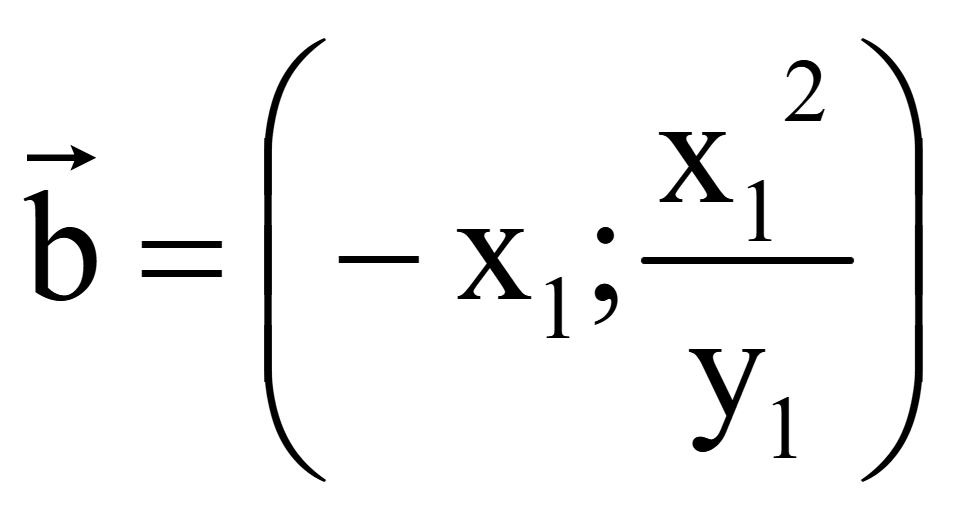
Координаты
второго вектора, перпендикулярного на плоскости вектору
= (x1; y1)
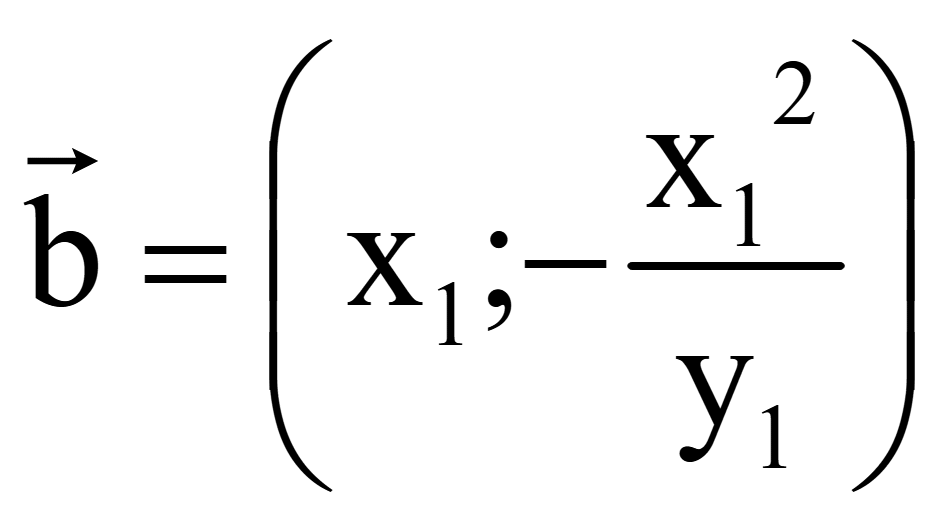
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
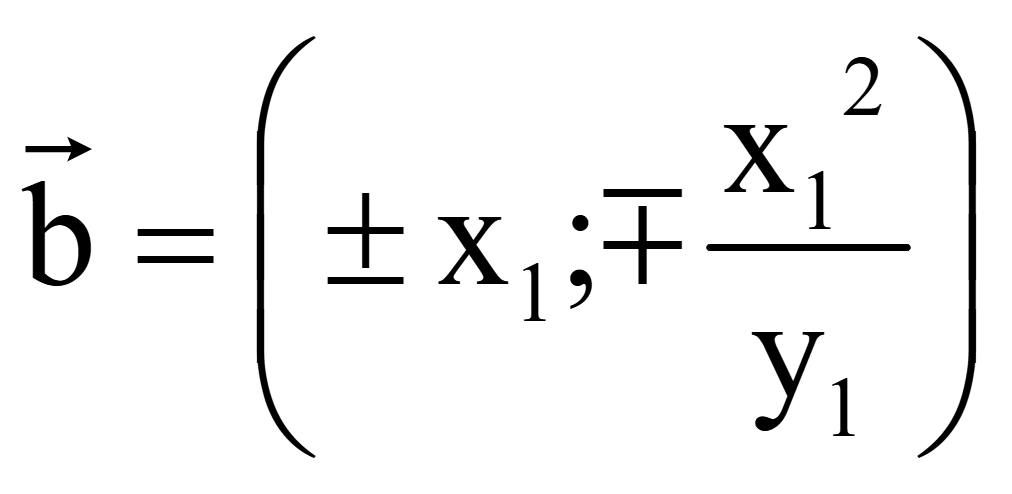
Элементы алгебры
- Сложение является двоичной операцией: за один раз можно сложить только пару.
- Коммутативность: сумма от перестановки слагаемых не изменяется a + b = b + a. Это ясно из правила параллелограмма: диагональ всегда одна и та же.
- Ассоциативность: сумма произвольного числа векторов не зависит от порядка их сложения (a + b)+ c = a +(b + c).
- Суммирование с нулевым вектором не меняет ни направление, ни длину: a +0= a .
- Для каждого вектора есть противоположный. Их сумма равна нулю a +(-a)=0, а длины совпадают.
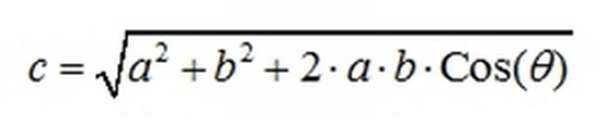 Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
Для вычитания можно использовать видоизмененное правило треугольника.
Умножение на скаляр
Результатом умножения на скаляр будет вектор.
Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.
Примеры скалярных величин в физике:
- масса,
- время,
- заряд ,
- длина,
- площадь,
- объем,
- плотность,
- температура,
- энергия.
Примеры:
- Перемещение равномерно движущегося тела равно произведению времени и скорости s = vt .
- Импульс тела — масса, умноженная на скорость p = mv .
- Второй закон Ньютона. Произведение массы тела на ускорение равно приложенной равнодействующей силе ma=F.
- Сила, действующая на заряженную частицу в электрическом поле, пропорциональна заряду F = qE.
Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.
Пример:
Работа является скалярным произведением силы и перемещения A = Fs .
Презентация на тему: » Векторы Понятие вектора Равенство векторов Откладывание вектора от данной точки Сумма двух векторов Законы сложения. Правило параллелограмма Сумма нескольких.» — Транскрипт:
1
Векторы Понятие вектора Равенство векторов Откладывание вектора от данной точки Сумма двух векторов Законы сложения. Правило параллелограмма Сумма нескольких векторов Вычитание векторов Умножение вектора на число

2
Понятие вектора Пусть на тело действует сила в 8Н. Стрелка указывает направление силы, а длина отрезка соответствует числовому значению силы. 8Н
3
Понятие вектора Рассмотрим произвольный отрезок. На нем можно указать два направления. Чтобы выбрать одно из направлений, один конец отрезка назовем НАЧАЛОМ, а другой – КОНЦОМ и будем считать, что отрезок направлен от начала к концу. Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется направленным отрезком или вектором.

4
Понятие вектора На рисунках вектор изображается отрезком со стрелкой Вектор АВ, А – начало вектора, В – конец. CD EF LK АВ АВ C D EF K L
5
Понятие вектора Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: Любая точка плоскости также является вектором, который называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: ММ = 0. a b c М

6
Понятие вектора Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ: АВ = а = АВ = 5 с = 17 Длина нулевого вектора считается равной нулю: ММ = 0. a М В А с

7
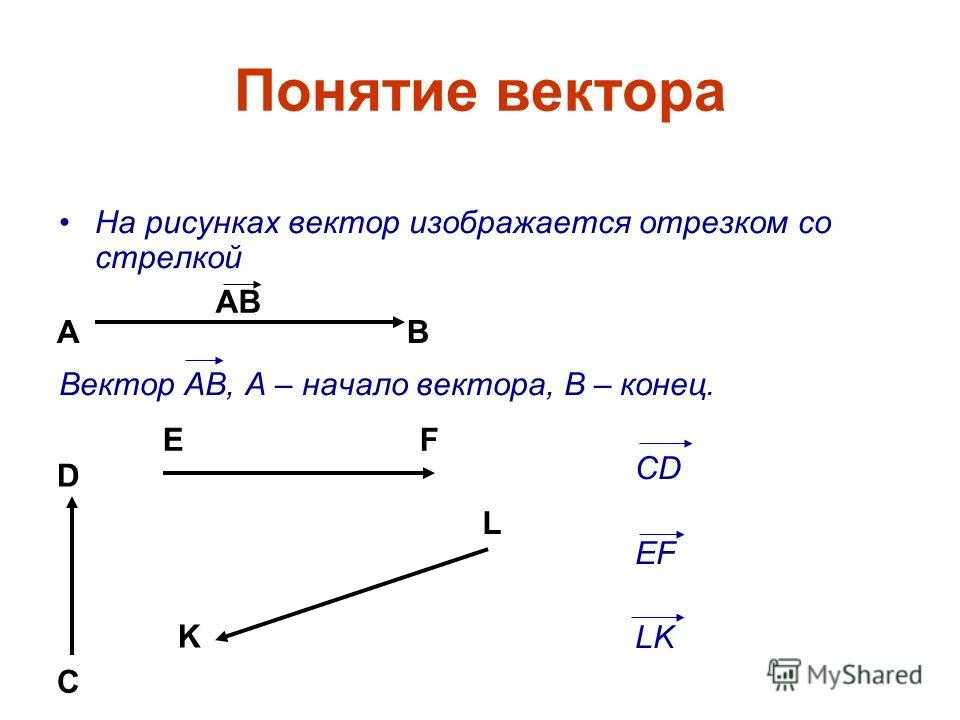
Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть сонаправленными или противоположно направленными. Нулевой вектор считается коллинеарным любому вектору. аb c d m n s L
8
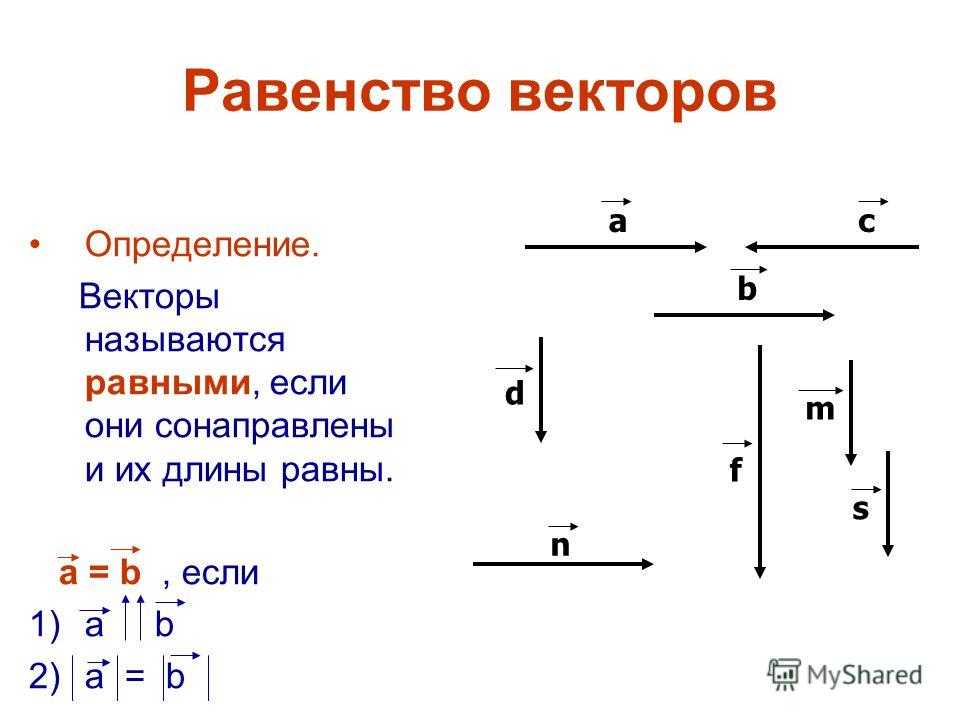
Равенство векторов Определение. Векторы называются равными, если они сонаправлены и их длины равны. а = b, если 1)а b 2)а = b аc b d m n s f
9
Откладывание вектора от данной точки Если точка А – начало вектора а, то говорят, что вектор а отложен от точки А. Утверждение: От любой точки М можно отложить вектор, равный данному вектору а, и притом только один. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой А а М а

10
Сумма двух векторов Рассмотрим пример: Сергей из дома(D) зашел к Саше(B), а потом поехал в кинотеатр(К). В результате этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК: DK=DB+BK. Вектор DK называется суммой векторов DB и BK. D B K

11
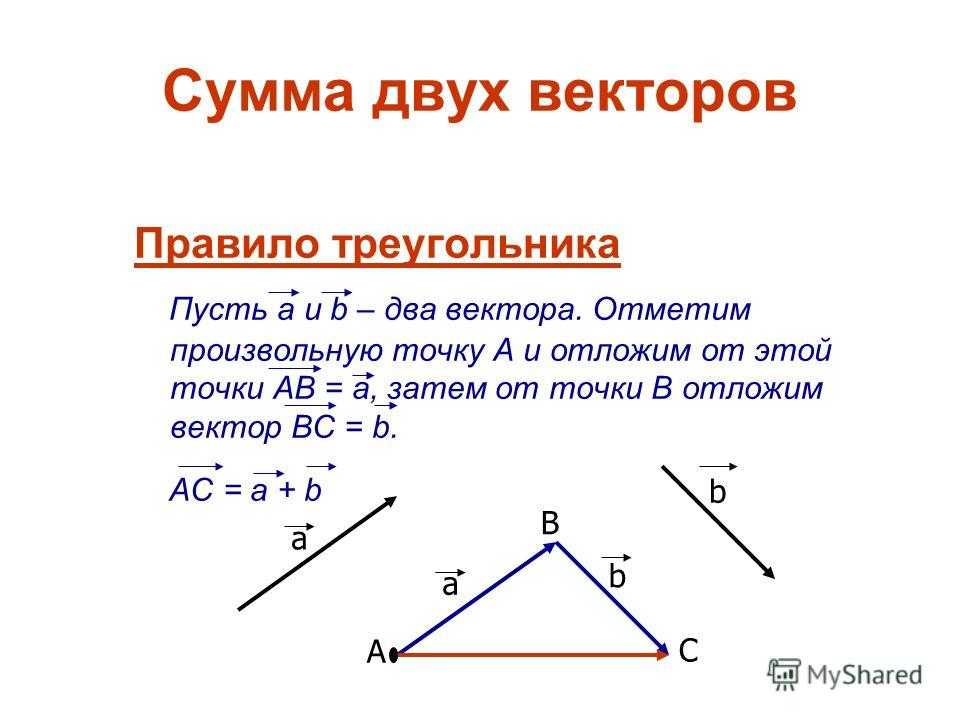
Сумма двух векторов Правило треугольника Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b. АС = а + b a b A a b B C
12
Законы сложения векторов 1) а+b=b+a (переместительный закон) Правило параллелограмма Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем вектор АD = b. На этих векторах построим параллелограмм АВСD. АС = АВ + BС = а+b АС = АD + DС = b+a 2) (а+b)+c=a+(b+c) (сочетательный закон) a a b b A DC B a b

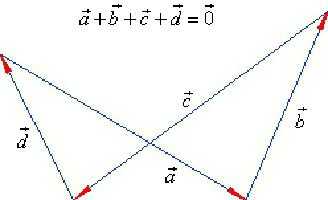
13
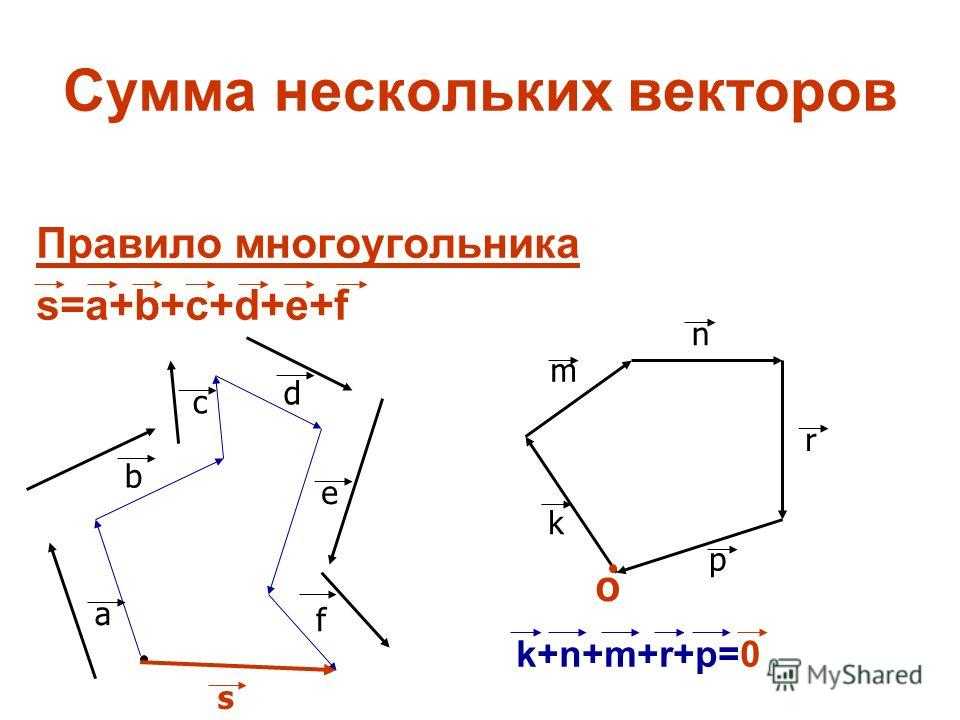
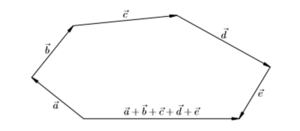
Сумма нескольких векторов Правило многоугольника s=a+b+c+d+e+f k+n+m+r+p=0 a b c d e f s k m n r p O
14
Противоположные векторы Пусть а – произвольный ненулевой вектор. Определение. Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены. a = АВ, b = BA Вектор, противоположный вектору c, обозначается так: -c. Очевидно, с+(-с)=0 или АВ+ВА=0 А B a b c -c

15
Вычитание векторов Определение. Разностью двух векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а. Теорема. Для любых векторов а и b справедливо равенство а — b = а + (-b). Задача. Даны векторы а и b. Построить вектор а – b. а а b -b a — b

16
Умножение вектора на число Определение. Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна вектору k а, причем векторы а и b сонаправлены при k0 и противоположно направлены при k

17
Умножение вектора на число Для любых чисел k, n и любых векторов а, b справедливы равенства: 1)(kn) а = k (na) (сочетательный закон) 2)(k+n) а = kа + na (первый распределительный закон) 3)K ( а+ b ) = kа + kb (второй распределительный закон) Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, p = 2( a – b) + ( c + a ) – 3( b – c + a ) = = 2a – 2b + c + a – 3b + 3c – 3a = — 5b + 4c

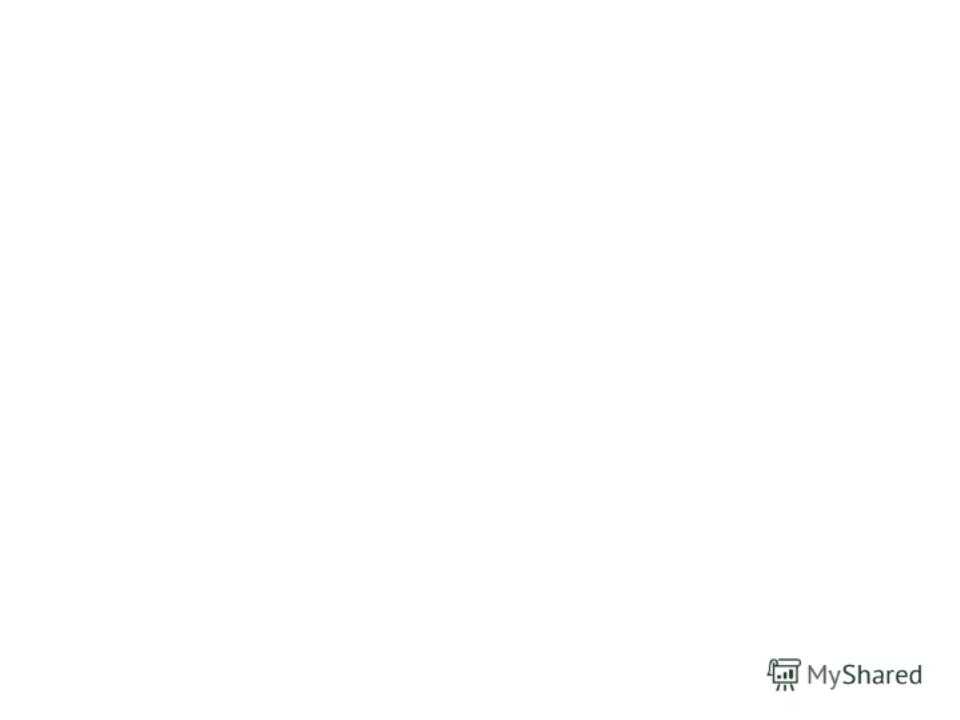

Сумма векторов
Существуют несколько правил для расчета суммы
- правило треугольника,
- правило многоугольника ,
- правило параллелограмма.
Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.
Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.
Результат двух перемещений или их сумма s = s1+ s2. Такой способ называется правилом треугольника.
Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».
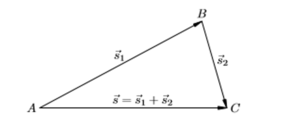
Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).
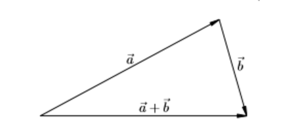
Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.
Примеры:
- Скорость тела, брошенного горизонтально, перпендикулярна ускорению свободного падения.
- При равномерном вращательном движении линейная скорость тела перпендикулярна центростремительному ускорению.
Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»
Предположим, что к точечному телу приложены силы F1 и F2.
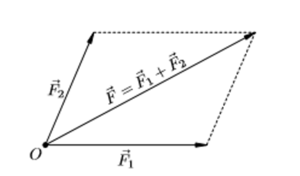
Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.
Длина в этом случае вычисляется по формуле
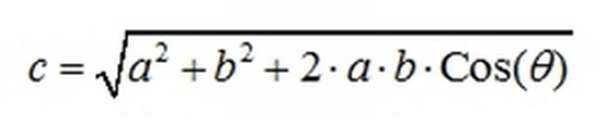
, где θ угол между сторонами.
Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.
2. Законы сложения векторов, правило параллелограмма
Законы сложения векторов
Для любых векторов , и справедливы следующие равенства:
– переместительный закон.
Доказательство: отложим из точки сначала вектор , получаем точку В, из нее откладываем вектор , получаем точку С и вектор .
Теперь отложим из точки А сначала вектор получим точку В, из нее отложим вектор, получим точку С и вектор .
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
Рис. 2
Откладываем из точки А вектор и вектор . Из точки В откладываем вектор , вектора и равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. , таким образом, мы доказали переместительный
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
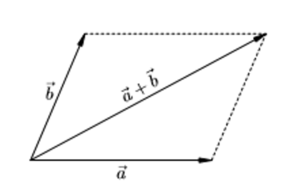
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
– сочетательный закон;
Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат (см. Рис. 4).
Рис. 4
В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору и получили результат: (см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.
Рис. 5
13 Координаты вектора, радиус-вектора и точки
Координаты
вектора — это координаты конца вектора, если начало вектора поместить
в начало координат.
Радиус-вектор
— это вектор, проведенный из начала координат к данной точке,
координаты радиус-вектора и точки равны.
Если
вектор
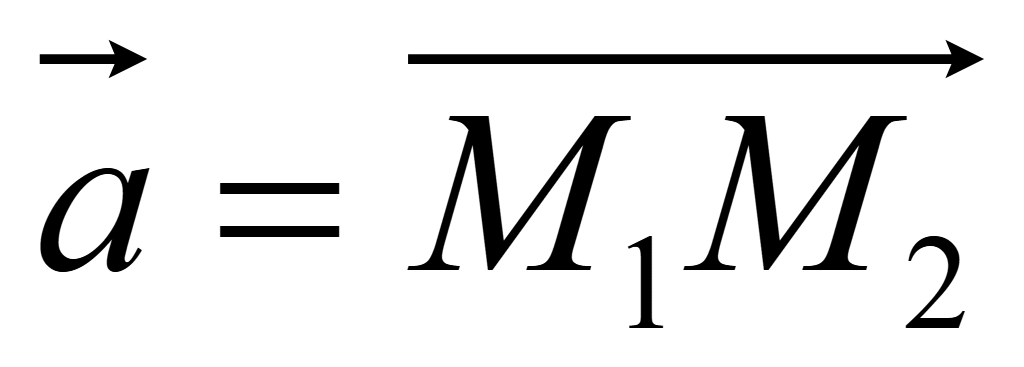
задан точками M1(x1;
y1; z1)
и M2(x2;
y2; z2),
то каждая из его координат равна разности соответствующих координат
конца и начала вектора
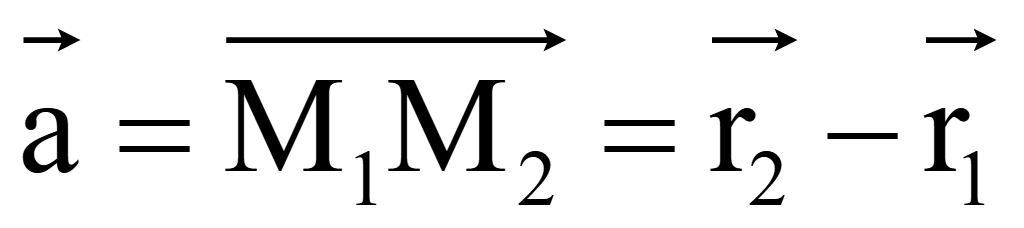 =
=
(x2
— x1;
y2
— y1;
z2
— z1)
= (xa; ya; za)
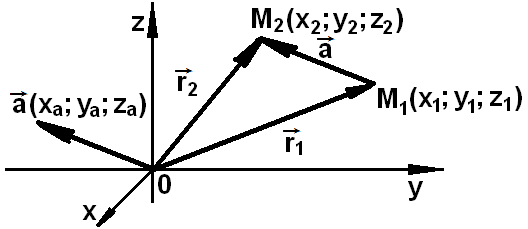
Для
коллинеарных векторов

=
(x1; y1;
z1) и
= (x2; y2;
z2), если
≠ 0, то существует единственное число k,
позволяющее выразить вектор
через
:
=
k
Тогда
координаты вектора
выражаются через координаты вектора
=
(kx1; ky1;
kz1) = (x2;
y2;
z2).
Отношение
соответствующих координат коллинеарных векторов
и
равно единственному числу k
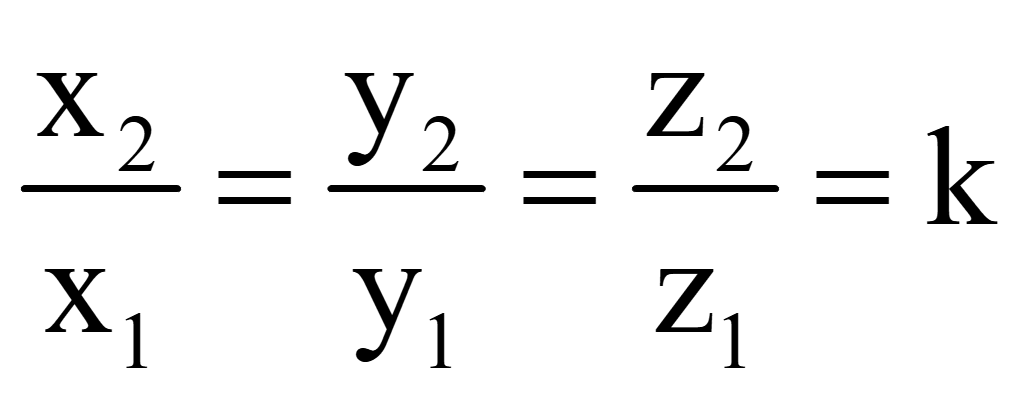
Если
отношение соответствующих координат векторов
и
равно единственному числу k, то
эти векторы коллинеарны. В противном случае векторы
и
неколлинеарны.