Комплексные числа

Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

Возведём его в квадрат, умножив на само себя:

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Расширенная комплексная плоскость. Сфера Римана

Из геометрии известно, что любой упорядоченной паре вещественных чисел соответствует точка $z$ на плоскости комплексного переменного. Определим
на комплексной плоскости бесконечно удаленную точку. Так условно будем называть «мысленную точку» $(x,y)$, координаты которой (обе сразу
или одна из них) — величины неограниченные, т.е. комплексные числа имеют формальный вид $z=x+i\infty$, $z=\infty+iy$ либо $z=\infty+i\infty$.
Тогда пишут $z=\infty$ (несобственное комплексное число), считая ее единственной бесконечно удаленной точкой.

Для несобственного комплексного числа понятия вещественной и мнимой части, а также понятие аргумента не вводятся; точнее говоря, объявляются
лишенными смысла (напомним, что понятие аргумента не имеет смысла и для числа 0). Что касается модуля числа $z=\infty$, то для него используется
символ $|\infty|=+\infty$.

Договорились, что имеют смысл следующие операции, в которых участвуют $z=\infty$ и собственное комплексное число $a$: $$
\frac{a}\infty=0,\quad\frac\infty{a}=\infty,\quad\frac{a}0=\infty.
$$ Такие операции, как $$
\infty\pm\infty,\quad 0\cdot\infty,\quad \dfrac00,\quad
\dfrac\infty\infty
$$ объявляются лишенными смысла.

Совокупность точек комплексной плоскости и бесконечно удаленной точки называется расширенной плоскостью комплексного переменного.

Наглядное представление о расширенной комплексной плоскости дает следующая интерпретация Римана (1826-1866).

Чтобы получить геометрическое изображение числа $\infty$, прибегают к представлению комплексных чисел точками сферы. Построим сферу (называемую сферой Римана) радиуса $r$, касающуюся плоскости $z$ в точке $z=0$ и отметим точку $N$ сферы, диаметрально противоположную началу
координат $O$.

Из точки $N(0,0,2r)$ сферы проведем проведем луч в любую точку $Z(x,y,0)$ плоскости $(x,y)$ и отметим точку $S$ пересечения данного луча и
сферы. Эта точка $S(\xi,\eta,\zeta)$ является новым геометрическим представлением комплексного числа $z$. В результате таких
построений лучей между точками плоскости $(x,y)$ и точками сферы устанавливается взаимно однозначное соответствие, называемое стереографической
проекцией, имеющей применение в картографии.

Точкам меридиана $NSO$ на сфере соответствуют точки луча $OZ$ на плоскости $(x,y)$, различным параллелям — круги на плоскости $(x,y)$.
Исключение составляет точка $N$. Северному полюсу $N$ сферы не соответствует пока никакое комплексное число. Однако точкам сферы, достаточно
близким к $N$, соответствуют точки $z$ плоскости, сколь угодно далеко отстоящие от начала координат, т.е. точка $z$ сколь угодно большого
модуля. Будем считать, что точке $N$ соответствует единственная точка $z=\infty$.

Покажем, что точка $z=\infty+\mathbf i \infty$ (или $z=x+\mathbf i \infty$, или $z=\infty+\mathbf i y$) будет при таком преобразовании переходить в точку $N(0,0,2r)$ и
наоборот. Координаты точек на такой сфере $(\xi,\eta,\zeta)$ связаны формулой
\begin{equation}\label{eq g1 p7 1}
\xi^2+\eta^2+(\zeta-r)^2=r^2\quad\hbox{или}\quad \xi^2+\eta^2=\zeta
(2r-\zeta).
\end{equation}

Из коллинеарности $NZ$ и $NS$ можно получить представление луча $NSZ$
$$
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-2r}{0-2r}.
$$
Отсюда можно получить координаты точек плоскости через координаты точек сферы:
\begin{equation}\label{eq g1 p7 2}
x=\frac{2r\xi}{2r-\zeta},\quad y=\frac{2r\eta}{2r-\zeta}.
\end{equation}

Составим
$$ x^2+y^2=\frac{4r^2(\xi^2+\eta^2)}{(2r-\zeta)^2}, $$
$$ x^2+y^2 = \frac{4r^2\zeta}{2r-\zeta}. $$
Тогда
можно выразить координату
$$
\zeta=\frac{2r(x^2+y^2)}{x^2+y^2+4r^2},
$$
и другие координаты
$$
\xi=\frac{4r^2x}{x^2+y^2+4r^2},\quad\eta=\frac{4r^2y}{x^2+y^2+4r^2}.
$$

Устремим $x\to\infty$, $y\to\infty$ (по отдельности или вместе), тогда $\xi\to0$, $\eta\to0$, $\zeta\to2r$, а это и есть точка $N$.

Некоторые сведения о комплексных числах подробнее изложены в курсе Высшей алгебры А.Ю. Утешева ( здесь).

Комплекснозначные функции действительного переменного.

Если каждому значению $t\in $ поставлено в соответствие комплексное число $z=z(t)$, то говорят, что на отрезке  задана комплекснозначная функция действительного переменного.

Пусть $\operatorname{Re}z(t) = x(t),\ \operatorname{Im}z(t) = y(t)$, тогда $z(t) = x(t)+iy(t)$. Функцию $z(t)$ можно рассматривать как вектор-функцию $z(t)=(x(t),y(t))$. Определения предела, непрерывности, производной для комплекснозначной функции аналогичны соответствующим определениям для вектор-функции.

Например, производная функции $z(t) = x(t) + iy(t)$ определяется формулой
$$
z'(t) = x'(t) + iy'(t).\label{ref25}
$$
Следовательно, производная $z'(t)$ существует, если существуют производные $x'(t)$ и $y'(t)$.

Применяя формулу \eqref{ref25} к функции $e^{it}=\cos t+i\sin t$, получаем $(e^{it})’=-\sin t+i\cos t=i^2\sin t + i\cos t = i(\cos t + i\sin t)$, то есть
$$
(e^{it})’=i e^{it}.\label{ref26}
$$

Таким образом, формула для производной комплексной функции $e^{it}$ имеет такой же вид, как и для функции $e^{\alpha t}$, где $\alpha\in\mathbb{R}$.

Определим теперь показательную функцию $\displaystyle e^{(\alpha+i\beta)t}$, где $\alpha,\beta$ — заданные действительные числа, $t$ — действительное переменное. Функция $f(t) = e^t$, где $t\in\mathbb{R}$, удовлетворяет условию
$$
f(t_1)f(t_2) = f(t_1+t_2).\label{ref27}
$$

Аналогично функция $e^{i\beta t}$, где $\beta\in\mathbb{R}$, обладает свойством \eqref{ref27} в силу первого из равенств \eqref{ref18}.

Поэтому функцию $e^{(\alpha+i\beta)t}$ естественно определить так, чтобы для нее выполнялось условие \eqref{ref27}, то есть
$$
e^{(\alpha+i\beta)t}=e^{\alpha t}e^{i\beta t}.\nonumber
$$

Используя формулу \eqref{ref15}, отсюда находим
$$
e^{(\alpha+i\beta)t} = e^{\alpha t} (\cos \beta t+i\sin\beta t).\label{ref28}
$$
Применяя к функции $e^{\lambda t}$, где $\lambda=\alpha+i\beta$, правило дифференцирования \eqref{ref25}, легко показать, что
$$
(e^{\lambda t})=\lambda e^{\lambda t},\quad \lambda=\alpha+i\beta.\label{ref29}
$$

По аналогии с производной неопределенный интеграл от комплекснозначной функции $z(t)=x(t)+iy(t)$ определяется формулой
$$
\int z(t) dt = \int x(t) dt + i\int y(t) dt.\nonumber
$$

Если комплексная функция $\omega(t) = \xi(t) + i\eta (t)$ такова, что $\omega'(t)=z(t)$, то
$$
\int z(t)=\int \omega'(t)dt=\int \xi'(t)dt+i\int \eta'(t)dt = \xi(t) + C_1 + i\eta(t)+iC_2.\nonumber
$$
Следовательно,
$$
\int z(t) dt = \omega(t) + C,\quad C = C_1+iC_2.\nonumber
$$
Применяя это утверждение к функции $e^{(\alpha+i\beta)t}$ и используя формулу \eqref{ref29}, получаем
$$
\int e^{(\alpha+i\beta)t}=\displaystyle \frac{e^{(\alpha+i\beta)t}}{\alpha+i\beta}+C_1+iC_2.\label{ref30}
$$

Выделяя в равенстве \eqref{ref30} действительные и мнимые части, находим
$$
\int e^{\alpha t}\cos\beta t dt + i\int e^{\alpha t}\sin\beta t dt = \frac{\alpha-i\beta}{\alpha^2+\beta^2}e^{\alpha t}(\cos\beta t+i\sin\beta t)+C_1+C_2,\nonumber
$$
откуда получаем
$$
\int e^{\alpha t}\cos\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\cos\beta t+\beta\sin\beta t)+C_1,\label{ref31}
$$
$$
\int e^{\alpha t}\sin\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\sin\beta t-\beta\cos\beta t)+C_2,\label{ref32}
$$

Заметим, что формула \eqref{ref31} была получена с помощью в .

История

Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Дж. Кардано (1545), который счёл их непригодными к употреблению.
Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни выражаются через кубические корни из мнимых величин), впервые оценил
Р. Бомбелли (1572).
Он же дал некоторые простейшие правила действий с комплексными числами.
Выражения вида , появляющиеся при решении квадратных и кубических уравнений, стали называть в XVI-XVII вв. «мнимыми».
Однако даже для многих крупных учёных XVII в. алгебраическая и геометрическая сущность мнимых величин представлялась неясной.
Известно, например, что Ньютон не включал мнимые величины в понятие числа, а Лейбницу принадлежит фраза: «Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием».

Зодача о выражении корней степени из данного числа была в основном решена в работах А. Муавра
(A. de Moivre, 1707, 1724) и Р. Котеса (R. Cotes, 1722).
Символ предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова imaginarius.
Он же высказал в 1751 мысль об алгебраической замкнутости поля комплексных чисел, к такому же выводу
пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит
Гауссу (1799). Он же ввёл в употребление термин «комплексное число» в 1831.
Полное геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе К. Весселя (С. Wessel, 1799).
Геометрическое представление комплексных чисел, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806 и 1814 работы Ж. Р. Аргана (J. R. Argand), повторявшей независимо выводы К. Весселя.

Арифметическая теория комплексных чисел как пар вещественных чисел была построена У. Р. Гамильтоном (1837).
Ему же принадлежит обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.

Возведение в степень и извлечение корня из комплексного числа

Возведение в натуральную степень равносильно умножению числа самого на себя $n$ раз: $$ z^n=z\cdot z\cdot\ldots\cdot z. $$

Формула для степени комплексного числа в показательной и тригонометрической формах: $$ z^n=(x+\mathbf i y)^n=\big(r(\cos\varphi+\mathbf i \sin\varphi)\big)^n=
\left(re^{\mathbf i \varphi}\right)^n=
$$ $$ =r^ne^{\mathbf i n\varphi}=r^n(\cos n\varphi+\mathbf i \sin n\varphi). $$ Отсюда получим формулу Муавра (1667-1754):
\begin{equation}\label{eq g1 p5 1}
(\cos\varphi+\mathbf i \sin\varphi)^n=\cos n\varphi+\mathbf i \sin n\varphi.
\end{equation}

В качестве $\varphi$ можно брать как $\mbox{Arg }z$, так и
$\arg z$, так как $$ e^{\mathbf i\mbox{Arg }z}=e^{\mathbf i \arg z+2\pi k\mathbf i}=e^{\mathbf i \arg z}e^{2\pi k\mathbf i}=e^{\mathbf i \arg z}, $$ ибо по формуле Эйлера $e^{2\pi k \mathbf i}=1$.

Пример. С помощью формулы Муавра выразить
$\cos3\varphi$ и $\sin3\varphi$ через $\cos\varphi$ и $\sin\varphi$.

О т в е т:
$\cos3\varphi=4\cos^3\varphi-3\cos\varphi, \,\, \sin3\varphi=-4\sin^3\varphi+3\sin\varphi$.

Число $w$ называется корнем натуральной степени из числа
$z\ne0$, если
\begin{equation}\label{g1 p5 2}
w^n=z.
\end{equation}
Обозначается $w=\sqrt{z}$, для $n=2$ имеем $w=\sqrt{z}$.

Вывод формулы $\sqrtz$. Пусть $$
\begin{array}{l}
z=r(\cos\varphi+\mathbf i \sin\varphi),\\
w=\rho(\cos\theta+i\sin\theta).
\end{array}
$$
Тогда
$$
\begin{array}{c}
w^n=\rho^n(\cos n\theta+\mathbf i \sin n\theta)= \\
=r(\cos\varphi+\mathbf i \sin\varphi).
\end{array}
$$
Приравнивая вещественные составляющие левой и правой частей, находим
$\rho^n=r$, а затем и $n\theta = \varphi+2\pi m=\arg z+2\pi k$. Получаем
$$
\begin{array}{l}
\rho=\sqrt{r}, \\
\theta=\dfrac1n\mbox{Arg }z=\dfrac1n\big(\arg z+2\pi k\big).
\end{array}
$$
Корень $n$-й степени из комплексного числа имеет $n$ различных
значений при $k=0,1,\ldots,n-1$:
$$
w_k=\sqrt{r(\cos\varphi+\mathbf i \sin\varphi)}=\!\sqrt{r}\left(\cos
\frac{\arg z+2\pi k}n+\mathbf i \sin\frac{\arg z+2\pi k}n\right).
$$

Геометрически эти $n$ значений корня изображаются вершинами правильного $n$-угольника с полярными координатами $\Big(\sqrtr,$ $\dfrac1n(\arg
z+2\pi k)\Big)$.

Пример. Найдем по формулам $\sqrt1=\{1,\mathbf i ,-1,-\mathbf i \}$. Эти точки
находятся в вершинах квадрата.

Из истории о комплексных числах

Развитие понятия числа от натуральных к действительным был связан как с нуждами практики, так и с нуждами самой математики. Древнегреческие математики считали «настоящими» лишь натуральные числа, но в житейских расчетах за тысячи лет до н. э. в Древнем Египте и в Древнем Вавилоне уже применялись дроби. Следующим значительным этапом в развитии понятия о числе было открытие отрицательных величин. Их ввели китайские математики за два века до н. э. а древнегреческий ученый Диофант в III веке н.э. уже мог производить действия над отрицательными числами. В тринадцатом веке стали извлекать квадратные корни из положительных чисел и определили, что с числами отрицательными эта операция неосуществима. Но в шестанадцатом веке в связи с познанием кубических уравнений математики столкнулись с данной проблемой. Исходя из этого итальянский алгебраист Дж. Кардано в 1545 году в собственном труде «Великое мастерство, либо «Об алгебраических правилах» внес предложение ввести числа новой сущности. Он назвал эти величины «чисто отрицательными» либо «софистически отрицательными», но находил их совсем ненужными и пытался не пользоваться ими. Но в первой половине 70-ых годов XVI века его соплеменник Р. Бомбелли опубликовал книгу, в которой были введены первые правила арифметических операций над подобными числами, вплоть до извлечения из них кубических корней.

Наименование «мнимые числа» во второй половине 30-ых годов семнадцатого века было введено философом и французским великим математиком Р. Декартом. А во второй половине 70-ых годов восемнадцатого века один из виднейших алгебраистов 18 века – Л. Эйлер – внес предложение применять первую букву французского слова imaginaire (мнимый) для обозначения числа I = √-1. Сам же термин «комплексное число» ввел в 1803 году Л. Карно, но в оборот он вошел лишь благодаря трудам К. Гаусса. Постепенно расширялась техника операций над комплексными числами. На рубеже 17 – 18 столетий была выстроена общая теория корней n-й степени сперва из отрицательных, а позже из любых комплексных чисел, а подробное геометрическое пояснение «мнимым» величинам дали в собственных трудах К. Вессель и Ж. Арган.

В конце 18 века великий математик из Франции Ж. Лагранж смог заявить, что матанализ уже не затрудняют мнимые величины. Посредством комплексных чисел обучились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами, а Я. Бернулли использовал комплексные числа для вычисления интегралов. Кроме этого посредством «мнимых» величин были решены задачи, которые связаны с гидродинамикой и картографией.

Алгебраическая форма комплексного числа

Комплексным числом $z$
называется выражение вида $z=x+\mathbf i y$, где $x$ и $y$ — вещественные числа, $\mathbf i$ — символ, называемый мнимой единицей, $\mathbf i^2=-1$.

Выражение $z=x+\mathbf i y$ называют алгебраической формой комплексного числа, $x$ называется вещественной частью числа $z$ и обозначается $\mathfrak{Re}(z)$ или $\mathfrak{Re}\,z$ ($\mathfrak{Re}$ — начальные буквы латинского слова realis — вещественный), $y$ называется мнимой частью $z$ и обозначается $\mathfrak{Im}(z)$ или $\mathfrak{Im}\,z$ ($\mathfrak{Im}$ — начальные буквы латинского слова imaginarius — мнимый).

Например, $\mathfrak{Re}(1-2\mathbf i)=1$, $\mathfrak{Im}(1-2\mathbf i)=-2$. Если $y=\mathfrak{Im}\,z=0$, то $z=x$ является вещественным числом, а если $\mathfrak{Re}\,z=x=0$ и $y\ne0$, то $z=\mathbf i y$ является чисто мнимым числом.

Два комплексных числа $z_1$ и $z_2$ равны тогда и только
тогда, когда $\mathfrak{Re} z_1=\mathfrak{Re} z_2$ и $\mathfrak{Im} z_1=\mathfrak{Im} z_2$ одновременно.

Сопряженным с комплексным числом $z=x+\mathbf i y$ называют
комплексное число вида $x-\mathbf i y$, его обозначают $\overline{z}=x-\mathbf i y$.

Свойства сопряжения
\begin{equation*}
\overline{\bar{z}}=z, \quad \overline{z_1z_2}=\bar{z}_1\bar{z}_2, \quad \overline{\frac{z_1}{z_2}}=\frac{\bar{z}_1}{\bar{z}_2}.
\end{equation*}

Комплексное число $-x-\mathbf i y=-z$ называется противоположным
комплексному числу $z=x+\mathbf i y$.
Их сумма равна так называемому нулевому комплексному числу $x+\mathbf i y+(-x-\mathbf i y)=0+\mathbf i 0$.

Для комплексных чисел $\alpha,\beta,\gamma$ выполняются следующие законы арифметики.

а) Коммутативный (переместительный) закон:

для сложения
$$ \alpha+\beta=\beta+\alpha;$$
для умножения
$$ \alpha\beta=\beta\alpha.$$

б) Ассоциативный (сочетательный) закон:

для сложения
$$ \alpha+\beta+\gamma=\alpha+(\beta+\gamma)=(\alpha+\beta)+\gamma=
\beta+(\alpha+\gamma);$$
для умножения
$$ \alpha\beta\gamma=\alpha(\beta\gamma)=(\alpha\beta)\gamma=\beta
(\alpha\gamma). $$

в) Дистрибутивный (распределительный) закон:
$$
\alpha(\beta+\gamma)=\alpha\beta+\alpha\gamma.
$$

Действия над комплексными числами, записанными в алгебраической форме $\alpha=a+b\mathbf i $, $\beta=c+d\mathbf i $, выражаются следующими формулами:

для сложения и вычитания
$$
\alpha\pm\beta=(a+b\mathbf i )\pm(c+d\mathbf i )=(a\pm c)+(b\pm d)\mathbf i ,
$$

для умножения (учитывая, что $\mathbf i ^2=-1$)
$$
\alpha\beta=(a+b\mathbf i )(c+d\mathbf i )=ac+ad\mathbf i +bc\mathbf i +bd\mathbf i ^2=(ac-bd)+(ad+bc)\mathbf i ,
$$
заметим также, что $\alpha\bar\alpha=a^2+b^2\in R$, $i^3=-i$, $i^4=1$, и, наконец,

для деления
$$
\frac\alpha\beta=\frac{\alpha\bar\beta}{\beta\bar\beta}=
\frac{(a+b\mathbf i )(c-d\mathbf i )}{c^2+d^2}=\frac{ac+bc\mathbf i -ad\mathbf i -bd\mathbf i ^2}{c^2+d^2}=
$$
$$
=\frac{ac+bd+(bc-ad)\mathbf i }{c^2+d^2}=\frac{ac+bd}{c^2+d^2}+
\frac{bc-ad}{c^2+d^2}\,\mathbf i .
$$

Множество всех комплексных чисел с арифметическими операциями образует поле комплексных чисел. Его обычно
обозначают символом $\mathbb C_{} $ (от лат. complex — тесно связанный).

Множество вещественных чисел $\mathbb R_{} $ является подмножеством множества комплексных чисел $\mathbb{C}$, то есть $\mathbb{R}\subset \mathbb{C}$.

Пример.
\begin{equation*}
\begin{split}
&z_1=-3+4\mathbf i , \,\, z_2=5-\mathbf i .\\
&z_1+z_2=2+3\mathbf i ,\,\, z_1-z_2=-8+5\mathbf i , \,\, z_1z_2=-11+23\mathbf i ,\\
&\overline{z}_2=5+\mathbf i , \,\, z_2\overline{z_2} =26, \,\, \frac{z_1}{z_2}=-\frac{19}{26}+\frac{17}{26}\mathbf i .
\end{split}
\end{equation*}

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).

Распишу подробно: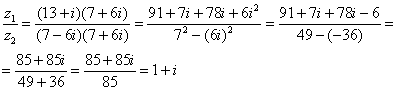

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Дополнение 1. Геометрический подход

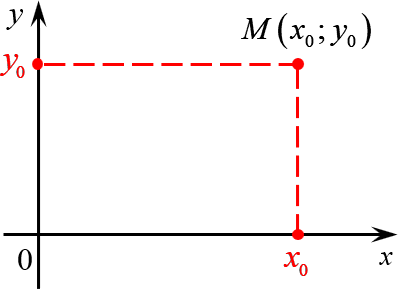
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

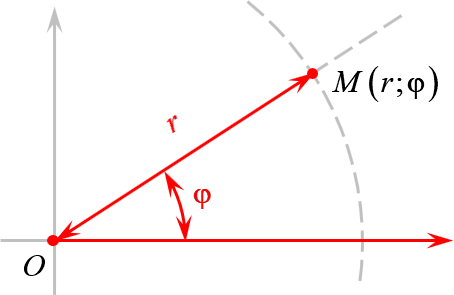
А есть полярная система координат, где точки задаются поворотом на угол $\varphi $ и расстоянием до центра $r$:

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

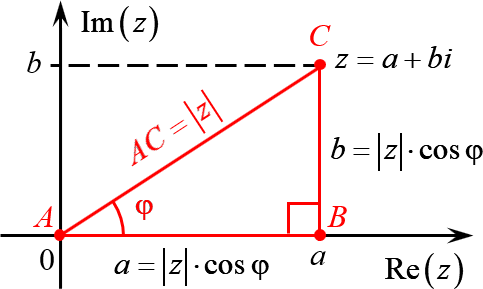
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $\angle BAC=\varphi $. Тогда:

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

Итак, мы перешли от пары $\left( a;b \right)$ к паре $\left( \left| z \right|;\varphi \right)$, где $\left| z \right|$ — модуль комплексного числа, $\varphi $ — его аргумент (проще говоря, угол поворота).

На практике основная трудность заключается именно в поиске подходящего аргумента.