Когда складываются степени? - ваша онлайн-энциклопедия

Преобразование дробей, содержащих степени

Степенные выражения могут содержать дроби со степенями или представлять собой такие дроби. К таким дробям в полной мере применимы любые из основных преобразований дробей, которые присущи дробям любого вида. То есть, дроби, которые содержат степени, можно сокращать, приводить к новому знаменателю, работать отдельно с их числителем и отдельно со знаменателем и т.д. Для иллюстрации сказанных слов рассмотрим решения нескольких примеров.

Пример.

Упростить степенное выражение .

Решение.

Данное степенное выражение представляет собой дробь. Поработаем с ее числителем и знаменателем. В числителе раскроем скобки и упростим полученное после этого выражение, используя свойства степеней, а в знаменателе приведем подобные слагаемые: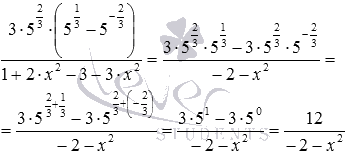

И еще изменим знак знаменателя, поместив минус перед дробью: .

Ответ:

Приведение содержащих степени дробей к новому знаменателю проводится аналогично приведению к новому знаменателю рациональных дробей. При этом также находится дополнительный множитель и выполняется умножение на него числителя и знаменателя дроби. Выполняя это действие, стоит помнить, что приведение к новому знаменателю может приводить к сужению ОДЗ. Чтобы этого не происходило, нужно, чтобы дополнительный множитель не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример.

Приведите дроби к новому знаменателю: а) к знаменателю a, б) к знаменателю .

Решение.

а) В этом случае довольно просто сообразить, какой дополнительный множитель помогает достичь нужного результата. Это множитель a0,3, так как a0,7·a0,3=a0,7+0,3=a. Заметим, что на области допустимых значений переменной a (это есть множество всех положительных действительных чисел) степень a0,3 не обращается в нуль, поэтому, мы имеем право выполнить умножение числителя и знаменателя заданной дроби на этот дополнительный множитель:

б) Присмотревшись повнимательнее к знаменателю, можно обнаружить, что
и умножение этого выражения на даст сумму кубов и , то есть, . А это и есть новый знаменатель, к которому нам нужно привести исходную дробь.

Так мы нашли дополнительный множитель . На области допустимых значений переменных x и y выражение не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби: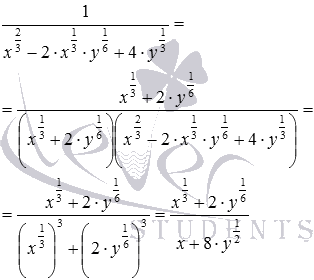

Ответ:

а) , б) .

В сокращении дробей, содержащих степени, также нет ничего нового: числитель и знаменатель представляются в виде некоторого количества множителей, и сокращаются одинаковые множители числителя и знаменателя.

Пример.

Сократите дробь: а) , б) .

Решение.

а) Во-первых, числитель и знаменатель можно сократить на наибольший общий делитель (НОД) чисел 30 и 45, который равен 15. Также, очевидно, можно выполнить сокращение на x0,5+1 и на . Вот что мы имеем:

б) В этом случае одинаковых множителей в числителе и знаменателе сразу не видно. Чтобы получить их, придется выполнить предварительные преобразования. В данном случае они заключаются в разложении знаменателя на множители по формуле разности квадратов:

Ответ:

а)
б) .

Приведение дробей к новому знаменателю и сокращение дробей в основном используется для выполнения действий с дробями. Действия выполняются по известным правилам. При сложении (вычитании) дробей, они приводятся к общему знаменателю, после чего складываются (вычитаются) числители, а знаменатель остается прежним. В результате получается дробь, числитель которой есть произведение числителей, а знаменатель – произведение знаменателей. Деление на дробь есть умножение на дробь, обратную ей.

Пример.

Выполните действия .

Решение.

Сначала выполняем вычитание дробей, находящихся в скобках. Для этого приводим их к общему знаменателю, который есть , после чего вычитаем числители:

Теперь умножаем дроби:

Очевидно, возможно сокращение на степень x1/2, после которого имеем .

Еще можно упростить степенное выражение в знаменателе, воспользовавшись формулой разность квадратов: .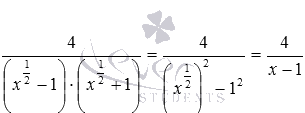

Ответ:

Пример.

Упростите степенное выражение .

Решение.

Очевидно, данную дробь можно сократить на (x2,7+1)2, это дает дробь . Понятно, что надо еще что-то сделать со степенями икса. Для этого преобразуем полученную дробь в произведение . Это дает нам возможность воспользоваться свойством деления степеней с одинаковыми основаниями: 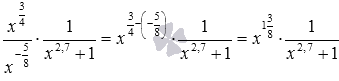. И в заключение процесса переходим от последнего произведения к дроби .

Ответ:

И еще добавим, что можно и во многих случаях желательно множители с отрицательными показателями степени переносить из числителя в знаменатель или из знаменателя в числитель, изменяя знак показателя. Такие преобразования часто упрощают дальнейшие действия. Например, степенное выражение можно заменить на .

Теория множеств

Вроде на этом можно остановиться, но есть еще одно элегантное доказательство. Дело в том, что математика, это не только цифры и числовые оси. Есть комбинаторика, теория функций, множество других разделов, где нужно значение 0 в степени 0.

Итак, есть три блогера смежной тематики: Я, Артур Шарифов и Топа. И есть две обалденные темы для ролика, например, искусственный интеллект и космос! Каждый записывает 1 ролик на 1 тему, повторяться, конечно, можно. Вопрос: сколькими вариантами они могут это сделать? Ну то есть все на одну тему, или двое одну, третий другую?

К чему эта задача? В теории множеств есть теорема, согласно которой множество с количеством элементов M можно отобразить на множество с количеством элементов N вот столькими вариантами N в степени M.

Здесь как раз множество блогеров (3 элемента) отображается на множество тем (2 элемента). В итоге получается 8 вариантов.

Если что, вот они все перед вами:

Дело в том, что бывают и пустые множества! И есть только один вариант отображения пустого множества на пустое. А это значит, что 0 в степени 0 и есть единица! Это чисто символическое доказательство, не такое серьезное. Но все равно, логично что, ноль блогеров может записать ноль роликов только одним способом.

Таблица примеров

Проверьте на рабочем листе книги Excel следующие примеры. Чтобы все заработало корректно, вам необходимо использовать смешанную ссылку при копировании формулы. Закрепите номер столбца, содержащего возводимое число, и номер строки, содержащей показатель. Ваша формула должна иметь примерно следующий вид: «=$B4^C$3».

Число / Степень

Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях. Не возникает проблем и с возведением любых чисел в целые показатели

А вот возведение отрицательного числа в дробную степень обернется для вас ошибкой, поскольку невозможно выполнить правило, указанное в начале нашей статьи про возведение отрицательных чисел, ведь четность — это характеристика исключительно ЦЕЛОГО числа.

Начальный уровень

Степень и ее свойства. Исчерпывающий гид (2019)

Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?

Чтобы узнать все о степенях, о том для чего они нужны, как использовать свои знания в повседневной жизни читай эту статью.

И, конечно же, знание степеней приблизит тебя к успешной сдаче ОГЭ или ЕГЭ и к поступлению в ВУЗ твоей мечты.

Let»s go… (Поехали!)

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Для этого нужно нажать CTRL+F5 (на Windows) или Cmd+R
(на Mac).

Арифметические действия с рациональными числами

Сложение

1. Чтобы найти сумму рациональных чисел с одинаковыми знаками, просто складываем их модули, затем перед получившимся результатом ставим их знак.

Например:

5 + 2 = + (5 + 2) = +7 = 7
13 + 8 + 4 = + (13 + 8 + 4) = +25 = 25
-9 + (-11) = – (9 + 11) = -20
-14 + (-53) + (-3) = – (14 + 53 + 3) = -70

Примечание: Если перед числом не стоит знак, то подразумевается “+“, т.е. оно является положительным. Также в полученном результате “плюс” можно опускать.

2. Для того, чтобы найти сумму рациональных чисел с разными знаками, мы к числу с большим модулем прибавляем те, у которых знак совпадает с ним, и отнимаем числа с противоположными знаками (величины берем абсолютные). Затем перед результатом ставим знак числа, из которого мы всё вычитали.

Например:

-6 + 4 = – (6 – 4) = -2
15 + (-11) = + (15 – 11) = +4 = 4
-21 + 15 + 2 + (-4) = – (21 + 4 – 15 – 2) = -8
17 + (-6) + 10 + (-2) = + (17 + 10 – 6 – 2) = 19

Вычитание

Для нахождения разности двух рациональных чисел к уменьшаемому прибавляем противоположное вычитаемому число.

Например:

9 – 4 = 9 + (-4) = 5
3 – 7 = 3 + (-7) = – (7 – 3) = -4

Если вычитаемых несколько, то сначала складываем все положительные числа, затем – все отрицательные (в т.ч. уменьшаемое). Таким образом мы получим два рациональных числа, разность которых находим по алгоритму выше.

Например:

12 – 5 – 3 = 12 – (5 + 3) = 4
22 – 16 – 9 = 22 – (16 + 9) = 22 – 25 = – (25 – 22) = -3

Умножение

Для нахождения произведения двух рациональных чисел просто перемножаем их модули, затем перед получившимся результатом ставим:

знак “+“, если у обоих сомножителей один и тот же знак;
знак “–“, если сомножители имеют разные знаки.

Например:

3 · 7 = 21
-15 · 4 = -60

Когда сомножителей больше двух, то:

Если все числа положительные – то результат будет со знаком “плюс”.
Если есть как положительные, так и отрицательные числа, то считаем количество последних:
- четное количество – результат с “плюсом”;
- нечетное количество – результат с “минусом”.

Например:

5 · (-4) · 3 · (-8) = 480
15 · (-1) · (-3) · (-10) · 12 = -5400

Деление

Как и в случае с умножением, выполняем действие с модулями чисел, затем ставим соответствующий знак с учетом правил, описанных в пункте выше.

Например:

12 : 4 = 3
48 : (-6) = -8
50 : (-2) : (-5) = 5
128 : (-4) : (-8) : (-1) = -4

Возведение в степень

Возведение рационального числа a в степень n – это то же самое, что и умножить это число само на себя n-ое количество раз. Пишется как a n.

При этом:

Любая степень положительного числа в результате дает положительное число.
Четная степень отрицательного числа положительна, нечетная – отрицательна.

Например:

26 = 2 · 2 · 2 · 2 · 2 · 2 = 64
-34 = (-3) · (-3) · (-3) · (-3) = 81
-63 = (-6) · (-6) · (-6) = -216

Что делать со степенями при сложении и вычитании числа?

Если , то (правило извлечения корня из дроби).

3. Если , то (правило извлечения корня из корня).

4. Если , то (правило возведения корня в степень).

5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.

6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.

7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:

(правило умножения корней),

(правило деления корней),

8. Правило вынесения множителя из-под знака корня. При .

9. Обратная задача — внесение множителя под знак корня. Например,

10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.

а) , так как .

Например, .

б)

Например,

в)

и т. д.

11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:

1) ;

2) ;

К началу страницы

Другие темы в блоке «Школьная математика»

Действия с дробями

Решение квадратных уравнений

Решение дробных уравнений с преобразованием в квадратное уравнение

Свойства степеней с одинаковыми показателями — Науколандия

Если умножаются (или делятся) две степени, у которых разные основания, но одинаковые показатели, то их основания можно перемножить (или поделить), а показатель степени у результата оставить таким же как у множителей (или делимого и делителя).

В общем виде на математическом языке эти правила записываются так:am × bm = (ab)mam ÷ bm = (a/b)m

При делении b не может быть равно 0, то есть второе правило надо дополнить условием b ≠ 0.

Примеры:23 × 33 = (2 × 3)3 = 63 = 36 × 6 = 180 + 36 = 21665 ÷ 35 = (6 ÷ 3)5 = 25 = 32

Теперь на этих конкретных примерах докажем, что правила-свойства степеней с одинаковыми показателями верны. Решим данные примеры так, как будто мы не знаем о свойствах степеней:23 × 33 = (2 × 2 × 2) × (3 × 3 × 3) = 2 × 2 × 2 × 3 × 3 × 3 = 8 × 27 = 160 + 56 = 216

Как мы видим, ответы совпали с теми, которые были получены, когда использовались правила. Знание этих правил позволяет упростить вычисления.

Обратите внимание, что выражение 2 × 2 × 2 × 3 × 3 × 3 можно представить в таком виде:(2 × 3) × (2 × 3) × (2 × 3). Это выражение в свою очередь есть нечто иное как (2 × 3)3, то есть 63

Это выражение в свою очередь есть нечто иное как (2 × 3)3, то есть 63.

Рассмотренные свойства степеней с одинаковыми показателями могут быть использованы в обратную сторону. Например, сколько будет 182?182 = (3 × 3 × 2)2 = 32 × 32 × 22 = 9 × 9 × 4 = 81 × 4 = 320 + 4 = 324

Свойства степеней также используются при решении примеров:= 24 × 36 = 24 × 34 × 3 × 3 = 64 × 32 = 62 × 62 × 32 = (6 × 6 × 3)2 = 1082 = 108 × 108 = 108 (100 + = 10800 + 864 = 11664

Корень

Обратное действие для возведения в степень это извлечение корня. Извлечение корня подразумевает под собой необходимость узнать, какое число возводили в ту или иную степень, чтобы получилось искомое число.

Если мы ищем квадратный корень из 4, то необходимо узнать, какое натуральное число возводилось в квадрат для получения числа 4.

$$\sqrt{4}=2$$

Что мы узнали?

Мы дали определение степени числа, разобрали, как расписывается степень в выражениях. Определили 6 свойств степени, привели формулировку и буквенную запись для каждой из них. Поговорили об обратном для степени действии – корне, о его значении и способах вычисления.

/5

Вопрос 1 из 5

Действия со степенями: правила вычисления степеней с разными основаниями или натуральными показателями по математике и порядок этого

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом: an = a * a * a * …an.

Причем, левая часть уравнения будет читаться, как a в степ. n.

Например:

23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
42 = 4 в степ. два = 4 * 4 = 16,
54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

an * am = (a)(n+m),
an : am = (a)(n-m),
(ab ) m=(a)(b*m).

Проверим на примерах:

23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично:

23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
(23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

33 + 24 = 27 + 16 = 43,
52 – 32 = 25 – 9 = 16

Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.. Как производить вычисления в более сложных случаях? Порядок тот же:

Как производить вычисления в более сложных случаях? Порядок тот же:

при наличии скобок – начинать нужно с них,
затем возведение в степень,
потом выполнять действия умножения, деления,
после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

Корень n-ой степени из числа a в степени m запишется в виде: am/n.
При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается:

A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.

И наоборот:

1 / A(-n) = An, 1 / 2(-3) = 23 = 8.

А если дробь?

(A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.

Основные виды преобразований степенных выражений

Со степенными выражениями можно выполнять любые из основных тождественных преобразований выражений. Например, можно раскрывать скобки, заменять числовые выражения их значениями, приводить подобные слагаемые и т.д. Естественно, при этом стоит надо соблюдать принятый порядок выполнения действий. Приведем примеры.

Пример.

Вычислите значение степенного выражения 23·(42−12).

Решение.

Согласно порядку выполнения действий сначала выполняем действия в скобках. Там, во-первых, заменяем степень 42 ее значением 16 (при необходимости смотрите возведение в степень), и во-вторых, вычисляем разность 16−12=4. Имеем 23·(42−12)=23·(16−12)=23·4.

В полученном выражении заменяем степень 23 ее значением 8, после чего вычисляем произведение 8·4=32. Это и есть искомое значение.

Итак, 23·(42−12)=23·(16−12)=23·4=8·4=32.

Ответ:

23·(42−12)=32.

Пример.

Упростить выражения со степенями 3·a4·b−7−1+2·a4·b−7.

Решение.

Очевидно, что данное выражение содержит подобные слагаемые 3·a4·b−7 и 2·a4·b−7, и мы можем привести их: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ:

3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Пример.

Представьте выражение со степенями в виде произведения.

Решение.

Справиться с поставленной задачей позволяет представление числа 9 в виде степени 32 и последующее использование формулы сокращенного умножения разность квадратов:

Ответ:

Также существует ряд тождественных преобразований, присущих именно степенным выражениям. Дальше мы их и разберем.

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии

Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики

Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Преобразование степеней с переменными в показателе

После знакомства со степенью с рациональным показателем вводится степень с иррациональным показателем, что позволяет говорить и о степени с произвольным действительным показателем. На этом этапе в школе начинает изучаться показательная функция, которая аналитически задается степенью, в основании которой находится число, а в показателе – переменная. Так мы сталкиваемся со степенными выражениями, содержащими числа в основании степени, а в показателе — выражения с переменными, и естественно возникает необходимость выполнения преобразований таких выражений.

Следует сказать, что преобразование выражений указанного вида обычно приходится выполнять при решении показательных уравнений и показательных неравенств, и эти преобразования довольно просты. В подавляющем числе случаев они базируются на свойствах степени и нацелены по большей части на то, чтобы в дальнейшем ввести новую переменную. Продемонстрировать их нам позволит уравнение 52·x+1−3·5x·7x−14·72·x−1=0.

Во-первых, степени, в показателях которых находится сумма некоторой переменной (или выражения с переменными) и числа, заменяются произведениями. Это относится к первому и последнему слагаемым выражения из левой части:52·x·51−3·5x·7x−14·72·x·7−1=0,5·52·x−3·5x·7x−2·72·x=0.

Дальше выполняется деление обеих частей равенства на выражение 72·x, которое на ОДЗ переменной x для исходного уравнения принимает только положительные значения (это стандартный прием решения уравнений такого вида, речь сейчас не о нем, так что сосредоточьте внимание на последующих преобразованиях выражений со степенями):

Теперь сокращаются дроби со степенями, что дает .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению , которое равносильно . Проделанные преобразования позволяют ввести новую переменную , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.

Как видите, преобразование степенных выражений с переменными в показателях степеней проводятся по принципам, разобранным в предыдущих пунктах.

Как пользоваться таблицей степеней числа два?

Первый столбец – это степень двойки, который одновременно, обозначает число бит, которое представляет число.
Второй столбец – значение двойки в соответствующей степени (n).

Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) – это 128
Третий столбец – максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).

Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число – это ноль, то максимальное число, которое можно представить с помощью семи бит 128 – 1 = 127 . Это и есть значение третьего столбца.

Степень двойки (n)	Значение степени двойки 2n	Максимальное число без знака, записанное с помощью n бит	Максимальное число со знаком, записанное с помощью n бит
1	–	–
1	2	1	–
2	4	3	1
3	8	7	3
4	16	15	7
5	32	31	15
6	64	63	31
7	128	127	63
8	256	255	127
9	512	511	255
10	1 024	1 023	511
11	2 048	2 047	1023
12	40 96	4 095	2047
13	8 192	8 191	4095
14	16 384	16 383	8191
15	32 768	32 767	16383
16	65 536	65 535	32767
17	131 072	131 071	65 535
18	262 144	262 143	131 071
19	524 288	524 287	262 143
20	1 048 576	1 048 575	524 287
21	2 097 152	2 097 151	1 048 575
22	4 194 304	4 194 303	2 097 151
23	8 388 608	8 388 607	4 194 303
24	16 777 216	16 777 215	8 388 607
25	33 554 432	33 554 431	16 777 215
26	67 108 864	67 108 863	33 554 431
27	134 217 728	134 217 727	67 108 863
28	268 435 456	268 435 455	134 217 727
29	536 870 912	536 870 911	268 435 455
30	1 073 741 824	1 073 741 823	536 870 911
31	2 147 483 648	2 147 483 647	1 073 741 823
32	4 294 967 296	4 294 967 295	2 147 483 647

Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных

Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения “плюс/минус”. Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.

Для этого же самого примера ( 27) семью битами можно записать максимум число +63, поскольку один бит занят знаком “плюс”. Но мы можем хранить и число “-63“, что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.

Вывод

Если мы находимся в рамках алгебры, простых арифметических вычислений, теории множеств, комбинаторики, находим суммы рядов, то без проблем можем считать это равным единице, и это во многих случаях будет даже упрощать наши вычисления.

Но в общем случае, особенно в рамках математического анализа, при вычислении пределов, говорят, что значение 0 в степени 0 – не определено. Его не существует, вот и все. И вообще, это только одна из многих неопределенностей, возникающих в матане, которая разрешается по-своему в каждом конкретном случае.

Так что чему равняется 0 в степени 0 зависит от контекста. Во многих случаях можно считать это единицей, но нужно помнить, что не во всех! И в разных языках программирования, разных калькуляторах тоже может быть по-разному. Где-то один, где-то не определено. В любом случае, практического применения у этого выражения нет, поэтому математики особо от него не страдают, хоть и иногда спорят, считать 0 в степени 0 равным единице, или нет. Но это не мешает быть ему таким интересным.