Теорема вейерштрасса о непрерывной функции на отрезке

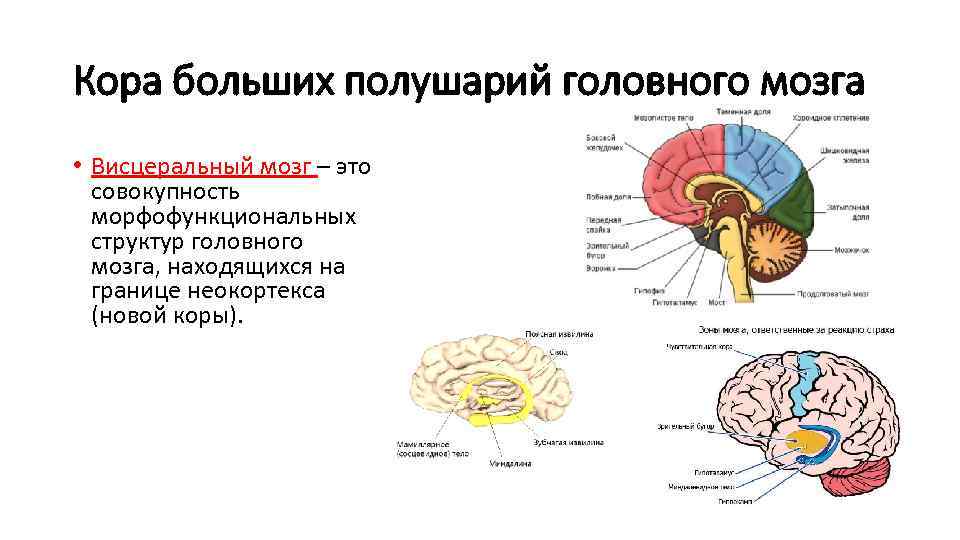
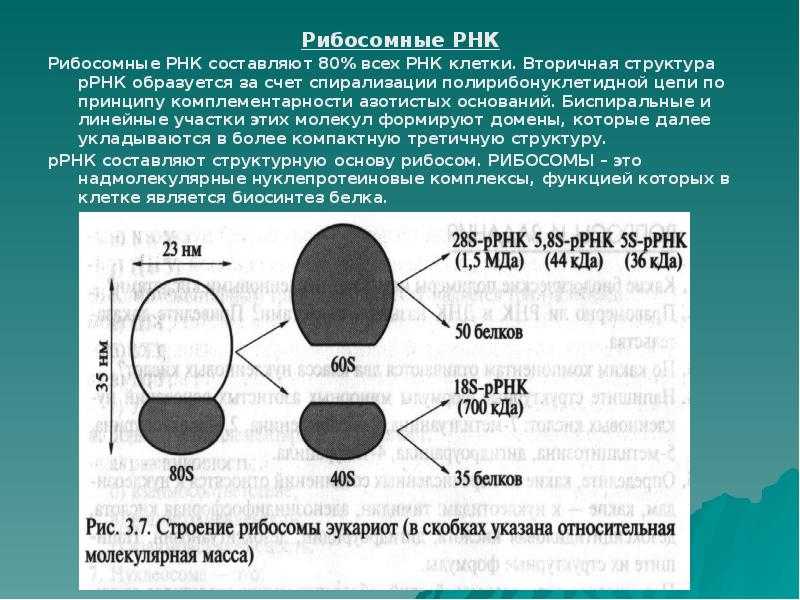
Слайды и текст этой презентации

Слайд 1

Текст слайда:

Бер Л.М Введение в анализ ТПУ Рег.№ 282 от 25.11.2009

МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Теорема 9. (Вейерштрасса) Всякая возрастающая числовая последовательность {xn} имеет предел: конечный, если она ограниченна сверху, и бесконечный, если она неограниченна сверху, причем Аналогично, если {xn} – убывающая последовательность, то существует (конечный или бесконечный) предели, следовательно, этот предел конечен, если последовательность ограниченна снизу, и бесконечный, если она неограниченна снизу.

Слайд 2

Текст слайда:

Бер Л.М Введение в анализ ТПУ Рег.№ 282 от 25.11.2009

КРИТЕРИЙ КОШИ

Теорема 10 (Критерий Коши). Для того чтобы последовательность {xn} сходилась к конечному пределу, необходимо и достаточно, чтобы . Последовательность, удовлетворяющая этому условию называется «фундаментальной последовательностью» или последовательностью, «сходящейся в себе».

Слайд 3

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Функции

Определение. Если каждому элементу х из множества X по определённому правилу или закону f ставится в соответствие один элемент у из множества Y, то говорят, что на множестве X задана функция f. Обозначение: f : X → Y или у = f(x). Способы задания функции:словесный,аналитический,табличный,графический. Определение. Пусть функция y = f(x) определена на множестве X, а функция z = ϕ(y) определена на множестве Y, причём область значений функции f содержится в области определения функцииϕ. Функция z =ϕ(f(x)) называется сложной функцией, или функцией от функции, или суперпозицией функций y = f(x) и z = ϕ(y). Обозначение: ϕ ° f, или ϕ (f) = ϕ (f (x)), ϕ — внешняя, f – внутренняя функция.

Слайд 4

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Основные элементарные функции

Постоянная у = с, с – const (константа);степенная функция у = xα, α ∈ R;показательная функция у = ах, а > 0, а ≠ 1;логарифмическая функция у = log a x, а > 0, а ≠ 1;тригонометрические функции у = sin x, у = cos x, у = tg x, y = ctg x;обратные тригонометрические функции у = arcsin x, у = arccos x, у = arctg x, у = arcctg x.

Слайд 5

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Основные элементарные функции

Слайд 6

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Основные элементарные функции

Слайд 7

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Основные элементарные функции

Слайд 8

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Основные элементарные функции

Слайд 9

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Классификация функций

Все функции, получаемые с помощью конечного числа алгебраических действий над основными элементарными функциями, а также суперпозицией (или наложением) этих функций, составляют класс элементарных функций. Функция видагде , называется целой рациональной функцией или алгебраическим многочленом (полиномом) степени n. Многочлен первой степени называется также линейной функцией. Функция, представляющая собой отношение двух целых рациональных функцийназывается дробно-рациональной функцией. Совокупность целых рациональных и дробно-рациональной функцией образует класс рациональных функций.

Слайд 10

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Классификация функций

Алгебраическая функция, не являющаяся рациональной функцией, называется иррациональной функцией. Всякая функция, не являющаяся алгебраической, называется трансцендентной. Трансцендентными в частности являются функции:Секанс: y = sec x, где sec x = 1/cos x.Косеканс: y = cosec x, где cosec x = 1/sin x.Синус гиперболический: y = sh x = (ex – e–x)/2.Косинус гиперболический: y = ch x = (ex + e–x)/2.Тангенс гиперболический: y = th x = (ex – e–x)/ (ex + e–x).Котангенс гиперболический: y = cth x = (ex + e–x)/ (ex – e–x).Секанс гиперболический: y = sch x = 2/ (ex + e–x).Косеканс гиперболический: y = csch x = 2/ (ex – e–x).

Слайд 11

Текст слайда:

Бер Л.М. Введение в анализ ТПУ Рег.№282 от 25.11.2009

Спасибо за внимание

Теорема Кантора о вложенных отрезках.

Назовем последовательность отрезков \(\Delta_{1},\Delta_{2},\ldots,\Delta_n,\ldots\), где \(\Delta_n=\), стягивающейся, если выполнены следующие условия:

1. каждый последующий отрезок принадлежит предыдущему, то есть
   $$
   \forall n\in\mathbb{N}\rightarrow\Delta_{n+1}\subset\Delta_{n};\label{ref19}
   $$
2. длина n-гo отрезка \(\Delta_n\) стремится к нулю при \(n\rightarrow\infty\), то есть
   $$
   \displaystyle \lim_{n\rightarrow\infty}(b_{n}-a_{n})=0.\label{ref20}
   $$

Условие \eqref{ref19} означает, что
$$
a_{1}\leq a_{2}\leq\ldots\leq a_{n}\leq a_{n+1}\leq\ldots\leq b_{n+1}\leq b_{n}\leq\ldots\leq b_{2}\leq b_{1}.\label{ref21}
$$

Теорема 2.

(Теорема Кантора)

Если последовательность отрезков является стягивающейся, то существует единственная точка, принадлежащая всем отрезкам этой последовательности.

\(\circ\) Существование. Из условия \eqref{ref21} следует, что

$$
\forall n\in\mathbb{N}\quad\forall m\in\mathbb{N}\rightarrow a_{n}\leq b_{m}.\label{ref22}
$$

По  из \eqref{ref22} заключаем, что существует \(sup\{a_n\}=c\), причем
$$
\forall n\in\mathbb{N}\rightarrow a_{n}\leq c\leq b_{n},\nonumber
$$
то есть существует точка с, принадлежащая всем отрезкам стягивающейся системы \(\{\Delta_n\}\).

Единственность. Пусть существуют две различные точки c и c’ принадлежащие всем отрезкам последовательности \(\{\Delta_n\}\), то есть \(c\in\Delta_n\) и \(c’\in\Delta_n\) при любом \(n\in\mathbb{N}\). Так как \(c\neq c’\), то либо \(c < c’\), либо \(c’ < c\). Пусть, например, \(c < c’\). Тогда \(a_{n}\leq c < c’\leq b_{n}\) при любом \(n\in\mathbb{N}\), откуда по свойствам неравенств \(b_{n}-a_{n}\geq c’-c=\alpha \ >0\) при любом \(n\in\mathbb{N}\), что противоречит условию \eqref{ref20}. Итак, \(\alpha=0\), то есть \(c’=c.\quad\bullet\)

Свойства пределов.

Появился новый математический объект, связывающий последовательности действительных чисел с пределами этих последовательностей (вообще говоря, множество значений элементов последовательности может не содержать значение предела). Возникает вопрос — а справедливы ли знакомые нам арифметические операции сложения, умножения и так далее для пределов? Оказывается да.

Формулировка немного корявая, но в принципе суть понятна. Справедливость всех этих операций строго доказывается. Так же вполне очевидно (но опять таки строго доказуемо), что если один предел последовательности больше другого, то начиная с некоторого номера, все элементы одной последовательности будут меньше элементов другой. Это все позволяет сформулировать так называемую теорему о трех последовательностях:

В принципе это утверждение интуитивно понятно, и доказывается тоже просто — нужно лишь показать, что элементы последовательности ${b_n}$ лежать в окрестности $A$, а они там лежат, потому, что элементы ${a_n},\ {c_n}$ лежат в этой же окрестности.

Следующим интересным свойством последовательностей является монотонность (опять вспоминаем функции). Монотонность тут означает, что все элементы последовательности либо возрастают (убывают) строго или не строго при возрастании индекса, т.е., например, $\forall n \in \mathbb{N} \ a_n \geq a_{n+1} $. Такие монотонные последовательности обладают неплохим свойством — мы можем узнать о сходимости последовательности просто проверим ее монотонность, благодаря теореме Вейерштрасса о сходимости монотонных последовательностей:

Аналогично и для монотонно убывающей последовательности. Тут важный момент, что последовательность может иметь предел равный бесконечности (с любым знаком). Теорема доказывается проверкой определения предела. Теперь (!!!) зная эту теорему можно ввести число $e$.

Сходимость такой последовательности можно доказать с помощью теоремы Вейерштрасса, так как элементы последовательности монотонно убывают.

Помимо монотонности последовательности могут быть фундаментальными:

Последовательность, для которой при любом эпсилон начиная с некоторого номера элементы последовательности будут различайся друг от друга меньше чем на эпсилон будем называть фундаментальной. Для таких фундаментальных последовательностей справедлив критерий Коши сходимости:

Это потрясающий критерий работающий в обе стороны.

Так же стоит упомянуть про частичные пределы и под-последовательности — во множестве элементов последовательности мы можем выделить другое множество и так же пронумеровать его элементы в возрастающем порядке (но уже с другим индексом), тогда такое новое множество можно назвать под-последовательностью. Очевидно, что если исходная последовательность имеет предел, то вокруг этого предела собирается бесконечное число элементов этой последовательности, а значит и бесконечное число элементов под-последовательности (как бы мы ее не задали). Поэтому можно ввести понятие частичного предела — как предела одной такой под-последовательности. Есть теорема о частичном пределе последовательности:

Обратное неверно — если существует частичный предел (но не единственный), то у исходной последовательности вообще может не быть предела.

До введения под-последовательностей мы ничего не могли сказать о том, если ли у ограниченной последовательности пределы или нет. Действительно, последовательность $a_n = (-1)^n$ ограничена, но предела не существует. Но, для ограниченных последовательностей мы можем судить о частичных пределах благодаря теореме Больцано-Вейерштрасса:

Доказывается эта теорема с помощью теоремы Кантора о вложенных отрезках — последовательностях вложенных отрезков имеет общую точку (не обязательно одну). Если для ограниченной последовательности мы докажем единственность частичного предела, то мы докажем и ее сходимость.

В принципе, это все основные свойства последовательностей в $\mathbb{R}$. Что было бы интересно отметить — ввели новый математический объект и сразу появились вопросы про его свойства. Поняли, что существуют такие последовательности, где вокруг некоторого значения собирается бесконечное число членов последовательности — как следствие, появилась потребность ввести понятие предела. И так далее

Вообще понятие предела последовательности очень важно для анализа, так как с помощью предела будут введены очень важные математические свойства функций, проливающих свет на многие интересные явления в том мире

Монотонная последовательность. Точные грани последовательности.

Последовательность \(\{x_{n}\}\) называют возрастающей (неубывающей), если для любого \(n\in\mathbb{N}\) выполняется неравенство
$$
x_{n+1}\geq x_{n}.\label{ref1}
$$
Аналогично последовательность\(\{x_{n}\}\) называют убывающей (невозрастающей), если для любого \(n\in\mathbb{N}\) справедливо неравенство
$$
x_{n+1}\leq x_{n}.\label{ref2}
$$
Если неравенство \eqref{ref1} можно записать в виде \(x_{n+1}>x_{n}\), а неравенство \eqref{ref2} — в виде \(x_{n+1} < x_{n}\), то последовательность \(\{x_{n}\}\) называют соответственно строго возрастающей и строго убывающей.

Возрастающую или убывающую последовательность называют монотонной, а строго возрастающую или строго убывающую — строго монотонной.

Если неравенство \eqref{ref1} выполняется при \(n\geq n_{0}\), то последовательность \(\{x_{n}\}\) называют возрастающей, начиная с номера \(n_{0}\) (при \(n\geq n_{0}\)). Аналогично вводятся понятия убывающей, строго убывающей и строго возрастающей последовательности, начиная с номера \(n_{0}\) (при \(n\geq n_{0}\)).

Для доказательства теоремы о пределе монотонной последовательности нам потребуются понятия точной верхней и нижней грани последовательности.

Точную верхнюю (нижнюю) грань множества значений последовательности \(\{x_{n}\}\) называют точной верхней (нижней) гранью последовательности и обозначают соответственно \(\sup{\{x_{n}\}}\) и \( \inf{\{x_{n}\}}\).

Определение точной верхней грани \(\sup{X}\) числового множества \(X,\) можно записать так:

$$
\displaystyle \{M=\sup X\}\Leftrightarrow\{\forall x\in X\rightarrow x\leq M\}\wedge\{\forall\varepsilon>0 \ \exists x_{\varepsilon}\in X:x_{\varepsilon}>M-\varepsilon\}.\label{ref3}
$$
Аналогично определение точной нижней грани \(\displaystyle \inf{X}\) числового множества \(X\) можно записать в виде
$$
\displaystyle \{m=\inf X\}\Leftrightarrow\{\forall x\in X\rightarrow x\geq m\}\wedge\{\forall\varepsilon>0\ \exists x_{\varepsilon}\in X:x_{\varepsilon} < m+\varepsilon\}.\label{ref4}
$$

Поэтому определения точной верхней и точной нижней граней последовательности можно записать в виде

$$
\Leftrightarrow\{\forall n\in N\rightarrow x_{n}\leq a\}\wedge\{\forall\varepsilon>0\ \exists N_{\varepsilon}:x_{N_{\varepsilon}}>a-\varepsilon\},\label{ref5}
$$
$$
\Leftrightarrow\{\forall n\in N\rightarrow x_{n}\geq b\}\wedge\{\forall\varepsilon<0\ \exists N_{\varepsilon}:x_{N_{\varepsilon}} < b+\varepsilon\}.\label{ref6}
$$

Таким образом, число \(a\) — точная верхняя грань последовательности \(\{x_{n}\}\), если выполняются условия:

1. все члены последовательности не превосходят \(a\), то есть
   $$
   \forall n\in N\rightarrow x_{n}\leq a;\label{ref7}
   $$
2. для каждого \(\varepsilon>0\) найдется член последовательности, больший \(a-\varepsilon\), то есть
   $$
   \forall\varepsilon>0 \ \exists N_{\varepsilon}:x_{N_{\varepsilon}}>a-\varepsilon.\label{ref8}
   $$

Аналогично разъясняется определение \eqref{ref6} точной нижней грани последовательности.

Контрольная работа «Предел последовательности» для студентов 1 курса

Контрольная работа «Предел последовательности» для студентов 1 курса (20 вариантов без решений) к учебнику: Конспект лекций по высшей математике./Д.Т. Письменный – М.: Айрис — пресс,2006.

    Основной формой обучения студента является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных и тестовых работ.

Студент может обращаться к преподавателю с вопросами для получения письменн…

Поделитесь с коллегами:

• 5
• Контрольная работа
• «Предел последовательности»
• Вычислить предел последовательности
• 1
• а)

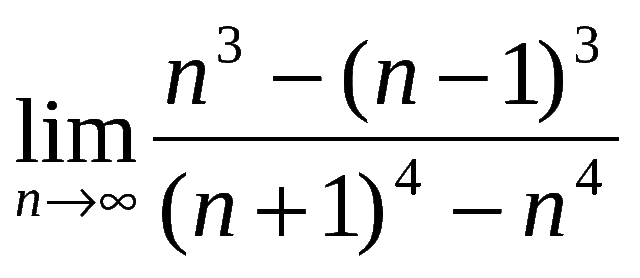
б)

1. в)
2. n
3. г)
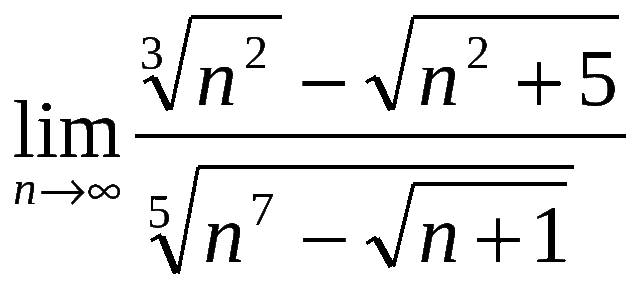
4. Вычислить предел последовательности
5. 2
6. а)

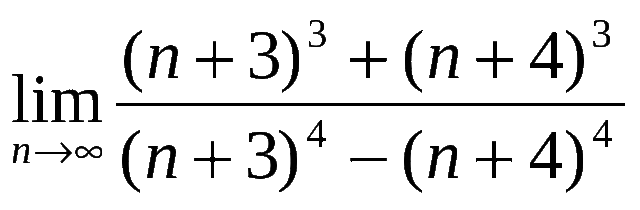
б)

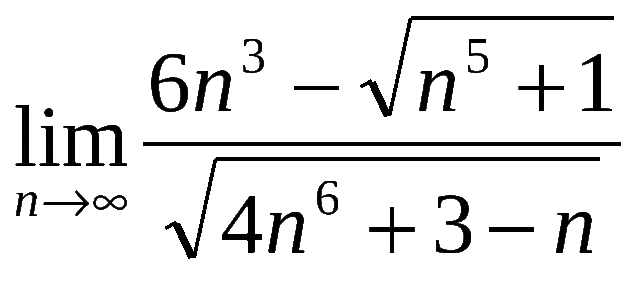
• в)
• г)
• Вычислить предел последовательности
• 3
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 4
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 5
• а)
• б)
• в)
• г)
• Контрольная работа № 4
• Вычислить предел последовательности
• 6
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 7
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 8
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 9
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 10
• а)
• б)
• в)
• г)
• Контрольная работа № 4
• Вычислить предел последовательности
• 11
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 12
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 13
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 14
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 15
• а)
• б)
• в)
• n
• г)
• Вычислить предел последовательности
• 16
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 17
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 18
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 19
• а)
• б)
• в)
• г)
• Вычислить предел последовательности
• 20
• а)
• б)
• в)
• г)
• Контрольная работа № 4

9.1Подпоследовательности и предельные точки

Подпоследовательности

Пусть у нас есть последовательность {an} и возрастающая
последовательность натуральных чисел {nk}. Тогда можно рассмотреть
последовательность {bk}, опредённую таким образом: для всех
натуральных k, bk=ank. Последовательность {bk} называется
подпоследовательностью последовательности {an}.

: Выделение подпоследовательности

Пример 1. Пусть an=2n и nk=2k. Тогда bk=a2k=22k задаёт
подпоследовательность исходной последовательности, состоящей из членов с
чётными номерами.

Пример 2. Пусть an=n3, nk=k2. Тогда bk=ak2=(k2)3=k6 задаёт
подпоследовательность исходной последовательности, состоящей из членов с
номерами, являющимися полными квадратами натуральных чисел.

Замечание 1. На {nk} накладываются два условия, оба важны. Во-первых, это
последовательность, то есть в ней бесконечно много элементов (значение nk
определено для всех натуральных k). Это означает, что в
подпоследовательности есть бесконечно много элементов, взятых из исходной
последовательности. Например, нельзя образовать подпоследовательность, взяв
первые три элемента исходной последовательности. Во-вторых, {nk}
возрастает — то есть мы должны брать элементы исходной последовательности в
том же порядке, в котором они были изначально (но можем некоторые
пропускать). Нельзя взять один и тот же элемент несколько раз или «вернуться
назад». Про подпоследовательность можно думать так, что мы выбросили из
исходной последовательности какое-то количество элементов (конечное или
бесконечное), но так, чтобы осталось бесконечно много элементов.

Пусть последовательность {an} обладает каким-нибудь из следующих
свойств:

• ограничена (сверху, снизу, просто);
• монотонна (возрастает, убывает, невозрастает, неубывает);
• имеет предел (конечный или бесконечный).

Тогда любая её подпоследовательность обладает тем же свойством (тоже
ограничена, тоже монотонна, тоже имеет предел, причём такой же, и т.д.)

Доказательство первых двух пунктов этого утверждения простое и я советую его
провести самостоятельно. Третий пункт вынесен в качестве задачи на семинары.
Обратное неверно: если подпоследовательность обладает каким-нибудь из этих
свойств (скажем, ограничена), это ничего не говорит про аналогичное свойство
исходной последовательности (приведите примеры).

Вопрос 1. Если последовательность неограничена, следует ли из этого, что любая её
подпоследовательность тоже неограничена?

Неверный ответ.
Попробуйте доказать

Верный ответ.
Действительно, можно рассмотреть неограниченную
последовательность an=((−1)n+1)n, у которой есть
тождественно нулевая подпоследовательность.

Предельные точки

an=(−1)na2k11a2k+1(−1)(−1)1(−1)предельными точками

Число A называется предельной точкой последовательности
{an} если существует такая подпоследовательность {bk},
bk=ank, что bk→A при n→∞.

Предел последовательности является её предельной точкой (можно выбрать
подпоследовательность, совпадающую с исходной последовательностью), но в отличие
от предела, предельных точек может быть несколько. Наоборот: по
, если у последовательности есть предел, то у
любой её подпоследовательности предел такой же. Значит, если предел есть, то
предельная точка единственна, и стало быть если предельных точек несколько, то
предела нет.

При решении некоторых задач удобным оказывается другое определение предельной
точки.

Число A называется предельной точкой последовательности
{an}, если для всякого ε> и всякого натурального N есть
такой номер n>N, что |an−A|<ε. Формально:
∀ε>∀N∈N∃n>N|an−A|<ε.

Сравните это определение с определением предела — в чём ключевое различие?

Упражнение 1. Докажите, что определения и
эквивалентны.

Есть ли последовательности, не имеющие предельных точек? Тут легко привести
пример — скажем, последовательность an=n обладает таким свойством: она
посещает каждое натуральное число ровно один раз, а потом уходит от него на
расстояние как минимум 1.

Заметим, что последовательсноть an=n неограничена. Бывают ли ограниченные
последовательности без предельных точек? Прежде, чем читать дальше, попробуйте
придумать такую.

Число e.

Рассмотрим последовательность \(\{x_{n}\}\), где
$$
x_{n}=\left(1+\displaystyle \frac{1}{n}\right)^{n},\nonumber
$$
и покажем, что эта последовательность возрастающая и ограниченная сверху. Используя формулу бинома Ньютона, получаем
$$
x_{n}=1+C_{n}^{1}\frac{1}{n}+C_{n}^{2}\frac{1}{n^{2}}+\ldots+C_{n}^{k}\frac{1}{n^{k}}+\ldots+\frac{1}{n^{n}},\nonumber
$$
где
$$
C_{n}^{k}=\displaystyle \frac{n(n-1)\ldots(n-(k-1))}{k!},\quad k=\overline{1,n},\quad C_{n}^{0}=1.\nonumber
$$

Запишем \(x_n\) следующем виде:
$$
x_{n}=1+\displaystyle \sum_{k=1}^{n}\frac{1}{k!}(1-\frac{1}{n})(1-\frac{2}{n})\ldots(1-\frac{k-1}{n});\label{ref16}
$$
тогда
$$x_{n+1}=1+\displaystyle \sum_{k=1}^{n+\perp}\frac{1}{k!}(1-\frac{1}{n+1})(1-\frac{2}{n+1})\ldots(1-\frac{k-1}{n+1}).\label{ref17}
$$
Все слагаемые в суммах \eqref{ref16} и \eqref{ref17} положительны, причем каждое слагаемое суммы \eqref{ref16} меньше соответствующего слагаемого суммы \eqref{ref17}, так как \(\displaystyle 1-\frac{m}{n}\,<\,1-\frac{m}{n+1}, \ m=\overline{1,n-1}\), а число слагаемых в сумме \eqref{ref17} на одно больше, чем в сумме \eqref{ref16}. Поэтому \(x_n < x_{n+1}\) для всех \(n\in\mathbb{N}\), то есть \(\{x_{n}\}\) — строго возрастающая последовательность. Кроме того, учитывая, что \(\displaystyle 0 < 1-\frac{m}{n} < 1 \ (m=\overline{1,n-1})\), из равенства \eqref{ref16} получаем \(x_{n} < 1+\displaystyle \sum_{k=1}^{n}\frac{1}{k!}\). Так как \(\frac{1}{k!}\leq \frac{1}{2^{k-1}}\) при \(k\in\mathbb{N}\), то, используя формулу для суммы геометрической прогрессии, получаем \(x_{n} < \displaystyle 1+\sum_{k=1}^{n}\frac{1}{2^{k-1}}=1+\frac{1-(1/2)^{n}}{1-1/2}=3-\frac{1}{2^{n-1}}\). Следовательно,
$$
x_{n}=\left(1+\frac{1}{n}\right)^{n}<3,\nonumber
$$
то есть \(\{x_{n}\}\) — ограниченная последовательность. По существует \(\underset{n\rightarrow\infty}{lim}x_n\). Этот предел обозначается буквой \(e\). Таким образом,
$$\displaystyle \lim_{n\rightarrow\infty}(1+\frac{1}{n})^{n}=e.\label{ref18}
$$

Число \(e\) является иррациональным, оно служит основанием натуральных логарифмов и играет важную роль в математике. Справедливо приближенное равенство
$$
e\approx 2,718281828459045\nonumber
$$

Признак сходимости монотонной последовательности.

Теорема 1.

Если последовательность \(\{{x_{n}}\}\) является возрастающей и ограниченной сверху, то существует
$$
\lim_{n\rightarrow\infty}x_{n}=\sup\{x_{n}\}.\nonumber
$$

Если последовательность \(\{x_{n}\}\) является убывающей и ограниченной снизу, то существует
$$
\lim_{n\rightarrow\infty}x_{n}=\inf\{x_{n}\}.\nonumber
$$

\(\circ\) Ограничимся доказательством теоремы для случая ограниченной сверху и возрастающей последовательности.

Если последовательность \(\{x_{n}\}\) ограничена сверху, то есть множество чисел \(x_{2},x_{2}, \ldots,x_{n}, \ldots\) ограничено сверху, то по существует точная верхняя грань этой последовательности, определяемая условиями \eqref{ref7}, \eqref{ref8}. Так как \(\{x_{n}\}\) — возрастающая последовательность, то
$$
\forall n\geq N_{\varepsilon}\rightarrow x_{N_{\varepsilon}}\leq x_{n}.\label{ref9}
$$

Из \eqref{ref7}-\eqref{ref9} следует, что
$$
\forall\varepsilon>0 \ \exists N_{\varepsilon}:\forall n\geq N_{\varepsilon}\rightarrow a-\varepsilon < x_{N_{\varepsilon}}\leq x_n\leq а,\nonumber
$$
то есть \(x_{n}\in U_{\varepsilon}(a)\).

Это означает, согласно определению предела, что
$$
\lim_{n\rightarrow\infty}x_{n}=a=\sup\{x_{n}\}.\quad\bullet\nonumber
$$

Замечание 1.

остается справедливой для последовательности, ограниченной сверху (снизу) и возрастающей (убывающей), начиная с некоторого номера.

Пример 1

Доказать, что если  \(x_n=\displaystyle \frac{a^{n}}{n!}\), где \(a>0\), то
$$
\lim_{n\rightarrow\infty}x_{n}=0.\nonumber
$$

\(\triangle\) Так как
$$
x_{n+1}=\frac{a}{n+1}x_{n},\label{ref10}
$$
то \(x_{n+1}\leq x_{n}\) при всех \(n\geq n_{0}\), где \(n_{0}=,\{x_{n}\}\) — убывающая при \(n\geq n_{0}\) последовательность. Кроме того, \(x_{n}\geq0\) при всех \(n\in\mathbb{N}\) то есть последовательность ограничена снизу. По последовательность \(\{x_{n}\}\) сходится. Пусть \(\displaystyle \lim_{n\rightarrow\infty} x_n=b\). Тогда, переходя к пределу в равенстве \eqref{ref10}, получаем \(b=0\). Итак,
$$
\lim_{n\rightarrow\infty}\frac{a^{n}}{n!}=0.\quad\blacktriangle\label{ref11}
$$

Замечание 2.

Утверждение \eqref{ref11} справедливо не только при \(a>0\), но и при любом \(a\in\mathbb{R}\), так как \(\displaystyle \left|\frac{a^{n}}{n!}\right|\leq\frac{|a|^{n}}{n!}\).

Пример 2

Последовательность \(\{x_{n}\}\)задается рекуррентной формулой

$$
x_{n+1}=\displaystyle \frac{1}{2}(x_{n}+\frac{a}{x_{n}}) ,\label{ref12}
$$

где  \(x_1>0, a>0\). Доказать, что
$$
\displaystyle \lim_{n\rightarrow\infty}x_{n}=\sqrt{a}.\label{ref13}
$$

\(\triangle\) Докажем сначала методом индукции, что

$$
\forall k\in\ N \rightarrow x_{k}>0.\label{ref14}
$$

В самом деле, из формулы \eqref{ref12} и условий \(x_{1}>0\), \(a>0\) следует, что \(x_{2}>0\). Предполагая, что \(x_{n}>0\), из равенства \eqref{ref12} получаем  \(x_{n+1}>0\). Утверждение \eqref{ref14} доказано.

Далее, применяя неравенство для среднего арифметического и среднего геометрического, из \eqref{ref12} получаем \(x_{n+1}=\displaystyle \frac{1}{2}(x_{n}+\frac{a}{x_{n}})\geq\sqrt{x_{n}\frac{a}{x_{n}}}=\sqrt{a}\) при \(n\in\mathbb{N}\), то есть
$$
\forall n\geq 2\rightarrow x_{n}\geq\sqrt{a}.\label{ref15}
$$

Итак, последовательность \(\{x_{n}\}\) ограничена снизу. Докажем, что она является убывающей. Запишем равенство \eqref{ref12} в виде
$$
x_{n+1}-x_n = \frac{a-x^2_n}{2x_n}\nonumber
$$
откуда в силу \eqref{ref14} и \eqref{ref15} получаем
$$
\forall n \geq 2 \rightarrow x_{n+1} \leq x_n,\nonumber
$$
то есть последовательность является убывающей при \(n\geq 2\). По существует \(\displaystyle\lim_{n\rightarrow\infty}{x_n}=\alpha\), где \(\alpha\geq\sqrt{a}>0\) в силу условия \eqref{ref15}. Переходя в равенстве \eqref{ref12} к пределу, получаем \(\displaystyle \alpha=\frac{1}{2}(\alpha+\frac{a}{\alpha})\) , откуда \(\alpha^{2}=a, \ \alpha=\sqrt{a}\), то есть справедливо утверждение \eqref{ref13}.\(\quad\blacktriangle\)

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность имеет конечный предел, равный точной верней границе, для неубывающей и точной нижней границе, для невозрастающей последовательности. Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность неубывающая, то для всех выполняются неравенства:(1.1)   .

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу. Это означает, что:

• для всех ,(1.2)   ;
• для любого положительного числа , существует такой номер , зависящий от , так что(1.3)   .

Поскольку последовательность неубывающая, то при имеем:. Здесь мы также использовали . Комбинируя с , находим:  при  . Поскольку  , то, или  при  . Это и означает, что число является пределом последовательности . Первая часть теоремы доказана.

2) Пусть теперь последовательность является невозрастающей ограниченной последовательностью:(2.1)    для всех .

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу. Это означает следующее:

• для всех выполняются неравенства:(2.2)   ;
• для любого положительного числа , существует такой номер , зависящий от , для которого(2.3)   .

Поскольку последовательность невозрастающая, то при имеем:. Здесь мы также использовали . Учитывая , находим:  при  . Поскольку  , то, или  при  . Это и означает, что число является пределом последовательности . Вторая часть теоремы доказана.

Теперь рассмотрим неограниченные последовательности.3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то для всех выполняются неравенства:(3.1)   .

Поскольку последовательность является неубывающей и неограниченной, то она неограниченна с правой стороны. Тогда для любого числа существует такой номер , зависящий от , для которого(3.2)   .

Поскольку последовательность неубывающая, то при имеем:. Здесь мы также использовали .

Итак, для любого числа существует такое натуральное число , зависящее от , так что для всех номеров выполняются неравенства:. Это означает, что предел последовательности равен плюс бесконечности:. Третья часть теоремы доказана.

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Аналогично предыдущему, поскольку последовательность невозрастающая, то(4.1)    для всех .

Поскольку последовательность является невозрастающей и неограниченной, то она неограниченна с левой стороны. Тогда для любого числа существует такой номер , зависящий от , для которого(4.2)   .

Поскольку последовательность невозрастающая, то при имеем:.

Итак, для любого числа существует такое натуральное число , зависящее от , так что для всех номеров выполняются неравенства:. Это означает, что предел последовательности равен минус бесконечности:. Теорема доказана.

Пример решения задачи

Все примеры Пользуясь теоремой Вейерштрасса, доказать сходимость последовательности:,   ,   . . . ,   , . . . После чего найти ее предел.

Решение

Представим последовательность в виде рекуррентных формул:,.

Докажем, что заданная последовательность ограничена сверху значением(П1)   . Доказательство выполняем методом математической индукции.. Пусть . Тогда. Неравенство доказано.

Докажем, что последовательность монотонно возрастает.;(П2)   . Поскольку , то знаменатель дроби и первый множитель в числителе положительные. В силу ограниченности членов последовательности неравенством , второй множитель также положителен. Поэтому. То есть последовательность является строго возрастающей.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Найдем этот предел. Обозначим его через . Воспользуемся тем, что. Применим это к , используя арифметические свойства пределов сходящихся последовательностей:. Условию удовлетворяет корень .

Ответ

.