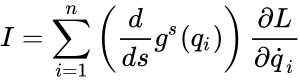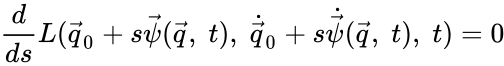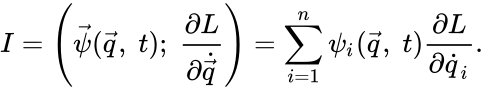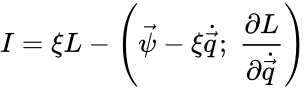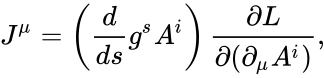Теорема нётер

Законы сохранения

В классической механике законы сохранения энергии, импульса и момента импульса выводятся из однородности/изотропности лагранжиана системы — лагранжиан (функция Лагранжа) не меняется со временем сам по себе и не изменяется переносом или поворотом системы в пространстве. По сути это означает то, что при рассмотрении некой замкнутой в лаборатории системы будут получены одни и те же результаты — вне зависимости от расположения лаборатории и времени проведения эксперимента. Другие симметрии лагранжиана системы, если они есть, соответствуют другим сохраняющимся в данной системе величинам (интегралам движения); например, симметрия лагранжиана гравитационной и кулоновской задачи двух тел приводит к сохранению не только энергии, импульса и момента импульса, но и вектора Лапласа — Рунге — Ленца.

Что такое эфир и откуда взялось понятие

Изучением эфира занимались многие выдающиеся ученые вплоть до начала XX века. Среди них был Дмитрий Менделеев, Хендрик Лоренц, Клерк Максвелл и многие другие. Первым же о теории эфира заговорил Рене Декар. Однако больше всего с эфиром связывают Николу Тесла, который не просто верил в существование эфира, но и проводил практические опыты.

Ученые давали разное определение эфиру, но большинство из них этим понятием называли некую материю, которая заполняет собой пространство между атомами и другими частицами. Соответственно, эфир заполняет собой всю вселенную.

Особый интерес к эфиру возник в XIX веке в рамках изучения волновой оптики. Открывая для себя свойства света, ученые пришли к выводу, что он имеет волновую природу. А волна не может распространяться в полном вакууме. Ей нужна определенная среда, в которой микрочастицы могут “плыть” точно так же, как и звуковые или любые другие волны. В итоге они приходили к выводу, что эфир — это неосязаемое, всепроникающее нечто, сверхтонкая материя.

Дмитрий Менделеев добавил эфир в периодическую таблицу химических элементов. В XX веке Ньютоний был удален

К примеру, Менделеев описывал его как сверхлегкий газ (самый легкий во вселенной). Его частицы обладают предельно высокой для газов скоростью поступательного движения. Еще одна особенность вещества, по мнению химика — сверхвысокая степень проницаемости. Не сомневаясь в его существовании, Менделеев добавил частичку эфира в свою таблицу и назвал ее “Ньютоний”.

В результате теория эфира стала не просто центральной темой научных изысканий, но и смогла объяснить многие явления. К слову, некоторые из них, после отказа от теории эфира, до сих пор не имеют научных объяснений.

В США

В 1933 г. Нетер как еврейка вынуждена была покинуть Германию и переехала в США, где преподавала в колледже Брин-Мор.

Когда нацисты пришли к власти в Германии в 1933 году, Нётер, как другие еврейские профессора в Гёттингене, была уволена. В октябре она уехала в США, чтобы стать приглашённым профессором математики в женском колледже Брин-Мор, штат Пенсильвания и лектором и исследователем в Институте перспективных исследований в Принстоне, Нью-Джерси. Она внезапно умерла от осложнений после операции на кисте яичника.

Эйнштейн писал вскоре после её смерти, что «Нётер была наиболее значимым творческим математическим гением, какой произошёл с начала высшего образования женщин».

[править] Научная карьера

Эмми Нётер родилась 23 марта 1882 года в Эрлангене в семье математика Макса Нётера.

Окончила университет в Эрлангене.

В 1907 году в университете Эрлангена защитила диссертацию по теории инвариантов.

Затем работала в Математическом институте Эрлангена без оплаты труда (так как считалось, что женщины не могут быть учёными, и поэтому женщины были исключены из академических позиций) в течении 7 лет.

В 1916 году перешла в Геттинген, своего рода тогдашнюю математическую столицу мира. Будучи уже выдающимся математиком, Нётер как женщина так и не получила академической должности и до 1922 года читала университетский курс алгебры вместо его официального руководителя Давида Гильберта.

В 1918 году вывела фундаментальную теорему теоретической физики, названную её именем. Это теорема установила связь между свойствами симметрии физической системы и законами сохранения и дала наиболее простой и универсальный метод получения законов сохранения в классической и квантовой физике, теории поля и пр

Особенно важное значение имеет теорема Нётер в квантовой теории поля, где законы сохранения, вытекающие из существования определенной группы симметрии, обычно являются главным источником информации о свойствах исследуемых объектов

В 1919 году — приват-доцент.

В −1922 годах — член Независимой социал-демократической партии Германии.

В −1926 годах проводила исследования в области теории идеалов.

В −1924 годах — член Социал-демократической партии Германии.

В −1933 годах — сверхштатный профессор Гёттингенского университета. Статус Нётер в качестве сверхштатного профессора Геттингенского университета не предоставлял академических прав и жалованья, однако позволил создать группу учеников, из которой позднее вышли крупнейшие алгебраисты.

С 1927 года вела разработку вопросов некоммутативных алгебр.

В −1929 годах приезжала в СССР, где читала лекции по алгебре в Московском университете и вела семинар по алгебраической геометрии в Коммунистической академии.

В 1932 году получила премию Аккермана-Тёбнера за достижения в математике.

В 1933 году Нётер, уволенная из университета как еврейка, была вынуждена покинуть гитлеровскую Германию и переехала в США, где преподавала в женском колледже Брин-Мор, а также стала приглашённым преподавателем Института перспективных исследований в Принстоне.

Внесла решающий вклад в развитие современной алгебры. Труды Нётер положили начало новому направлению алгебраических исследований — общей (абстрактной) алгебры: общая теория полей, колец, идеалов.

Умерла 14 апреля 1935 года в Брин-Море, штат Пенсильвания.

Альберт Эйнштейн написал по случаю её смерти некролог, в котором назвал Нётер «величайшим творческим математическим гением, явившимся миру с тех пор, как для женщин открылось высшее образование».

Её младший брат — математик Фриц Нётер — уехал в СССР, где в сентябре 1941 года был расстрелян.

Вклад в мировую науку

Нетер внесла решающий вклад в развитие современной алгебры. Ее труды положили начало новому направлению алгебраических исследований, известному под названием общей, или абстрактной алгебры (общая теория полей, колец, идеалов). Она была пионером в общей теории идей, а с 1926 и далее, инициировала достижения в некоммутативной алгебре.

Нетер принадлежит названная ее именем фундаментальная теорема теоретической физики (1918), которая установила связь между свойствами симметрии физической системы и законами сохранения и дала наиболее простой и универсальный метод получения законов сохранения в классической и квантовой физике, теории поля и т. д

Особенно важное значение имеет теорема Нетер в квантовой теории поля, где законы сохранения, вытекающие из существования определенной группы симметрии, обычно являются главным источником информации о свойствах исследуемых объектов

Масштабы и значимость её вклада в математику не могут быть точно представлены только её научными трудами. Большая часть её работ появились в публикациях студентов и коллег. Много раз предложение или даже случайное замечание показывали её большую проницательность и стимулировали другого учёного завершить работу и усовершенствовать научное представление.

Биография

Первоначально изучала языки, планируя стать преподавателем английского и французского . С этой целью добилась разрешения посещать лекции в Эрлангенском университете, где работал её отец, вначале вольнослушательницей (1900), а с 1904 года, когда разрешили женское обучение, зачислена официально. Однако в университете лекции по математике привлекали Эмми больше, чем любые другие. Она стала ученицей математика Пауля Гордана, под руководством которого защитила в 1907 году диссертацию по теории инвариантов.

Уже в 1915 году Нётер внесла вклад в разработку Общей теории относительности; Эйнштейн в письме к мировому лидеру математиков Давиду Гильберту выразил восхищение «проницательным математическим мышлением» Нётер.

В 1916 году Нётер переехала в Гёттинген, где знаменитые математики Давид Гильберт и Феликс Клейн продолжали работы по теории относительности, и знания Нётер в области теории инвариантов были им нужны. Гильберт оказал на Нётер огромное влияние, сделав её сторонницей аксиоматического метода. Он пытался сделать Нётер приват-доцентом Гёттингенского университета, но все его попытки провалились из-за предрассудков профессуры, в основном в области гуманитарных наук. Стала известна фраза Гильберта:

YES WE CAN — New Approaches — Entertainment — EMMY WINNER

Все видео

Нётер тем не менее, не занимая никакой должности, часто читала лекции за Гильберта. Лишь по окончании Первой мировой войны она смогла стать приват-доцентом в 1919 году, затем сверхштатным профессором (1922).

Самый плодотворный период научной деятельности Нётер начинается около 1920 года, когда она создаёт целое новое направление в абстрактной алгебре. С 1922 года она работает профессором Гёттингенского университета, возглавляет авторитетную и быстро растущую научную школу.

Современники описывают Нётер как на редкость умную, обаятельную и приветливую женщину. Её женственность проявлялась не внешне, а в трогательной заботе об учениках, всегдашней готовности помочь им и коллегам. В числе ее преданных друзей были ученые с мировым именем: Гильберт, Герман Вейль, Эдмунд Ландау, нидерландский математик Л. Брауэр, советские математики П. С. Александров, П. С. Урысон и многие другие.

Нётер придерживалась социал-демократических взглядов. На протяжении 10 лет жизни она сотрудничала с математиками СССР; в 1928—1929 учебном году читала лекции в Московском университете, где она оказала влияние на Л. С. Понтрягина и особенно на П. С. Александрова, до этого часто бывавшего в Гёттингене. П. С. Александров вспоминал:

В 1932 году Нётер, совместно со своим учеником Эмилем Артином, получает премию Аккермана-Тёбнера за достижения в математике.

После прихода нацистов к власти в 1933 году Нётер, как еврейке, пришлось эмигрировать в США, где она стала преподавателем женского колледжа в Брин-Море (Пенсильвания) и приглашённым преподавателем Института перспективных исследований в Принстоне. Младший брат Эмми, одарённый математик Фриц Нётер, уехал в СССР, где был расстрелян в сентябре 1941 года за «антисоветские настроения».

Несмотря на блестящие математические достижения, личная жизнь Нётер не сложилась. Непризнание, изгнание, одиночество на чужбине, казалось бы, должны были испортить её характер. Тем не менее, она почти всегда выглядела спокойной и доброжелательной. Герман Вейль писал, что даже счастливой.

В 1935 году Эмми Нётер умерла после неудачной операции по удалению раковой опухоли.

Академик П. С. Александров писал:

А. Эйнштейн в заметке на её смерть отнёс Нётер к величайшим творческим гениям математики.

Теория энергетического заговора

В начале XX века после появления теории относительности Эйнштейна на эфир в научном сообществе было наложено табу. Любые упоминания о нем в учебниках химии и физики были незамедлительно удалены. Сами же ученые, которые не спешили отвергать наличие этого вещества, подвергались жесткой цензуре и, фактически, лишались возможности добиться успехов и признания в научном сообществе.

Существует теория, согласно которой за этим стояли крупные корпорации и бизнесмены-нефтяники. Причем сам Эйнштейн, согласно этой теории, лоббировал их интересы в научном мире. Доводом послужила тесная связь ученого с домом Ротшильдов и его финансирование банкирами.

В то же время известно, что противником Тесла был другой, не менее известный банкир — Морган. Примечателен тот факт, что последний финансировал Николу Тесла до тех пор, пока не выяснил, что изобретатель работает, фактически, над крахом его бизнес-империи. После этого он приложил все усилия, чтобы Теслу больше вообще никто не финансировал. Разумеется, бесплатная энергия могла поставить крест не только на бизнесе отдельных корпораций, но и экономике целых стран.

Первый в мире электромобиль, разработанный Генри Фордом

Также сторонники теории заговора проводят аналогии с электромобилями Генри Форда. Совместно с Томасом Эдиссоном им было построена и успешно испытана как минимум одна машина, хотя некоторые источники указывают не несколько автомобилей с электродвигателями. Сам Генри рассказывал о перспективности этих проектов в СМИ и обещал в скором будущем начать массовое производство таких машин. Однако, с определенного момента СМИ перестали вообще упоминать об Edison-Ford. Мастерские были уничтожены пожаром, а и сам Генри Форд к идее электромобилей больше никогда не возвращался.

Отказ от них в пользу ДВС связывают с договором между Фордом и нефтяными картелями, которые прекрасно понимали перспективность автомобилестроения и выгоду, которую они получат от машин, потребляющих нефтепродукты. Но, уже сейчас можно с уверенностью говорить, что выбор в пользу ДВС был абсолютно неверным решением. К примеру, электромобиль Тесла бесшумно разгоняется до 100 км/ч за 2,3 секунды, при этом стоит всего 130.000$. Такие же динамические показатели имеет Bugatti Chiron, вот только разгоняется с грохотом, а его стоимость достигает 2,5 млн. долларов. Потребляет такой суперкар десятки литров высокооктанового топлива на 100 км.

Формулировка

Классическая механика

Каждой однопараметрической группе диффеоморфизмов , сохраняющих функцию Лагранжа, соответствует первый интеграл системы, равный

В терминах инфинитезимальных преобразований, пусть инфинитезимальное преобразование координат имеет вид

и функция Лагранжа инвариантна относительно этих преобразований, то есть

Тогда у системы существует первый интеграл, равный

Теорему можно обобщить на случай преобразований, затрагивающих также и время, если представить её движение как зависящее от некоторого параметра , причем в процессе движения . Тогда из преобразований

следует первый интеграл

Теория поля

Теорема Нётер допускает прямое обобщение на случаи систем с бесконечным числом степеней свободы, примером которых являются гравитационное и электромагнитное поле. А именно, пусть функция Лагранжа системы зависит от потенциалов, зависящих, в свою очередь, от координат. Функционал действия будет иметь вид

Пусть однопараметрическая группа диффеоморфизмов пространства потенциалов сохраняет функцию Лагранжа, тогда сохраняется вектор

называемый вектором потока Нётер. По повторяющимся индексам подразумевается суммирование, .
Смысл сохранения вектора потока Нётер в том, что

поэтому поток через любую замкнутую поверхность в пространстве координат равен 0. В частности, если выделить среди координат одну, называемую временем, и рассмотреть гиперплоскости постоянного времени, то поток через такую гиперплоскость постоянен во времени, при условии достаточно быстрого спадения поля на бесконечности и некомпактности гиперповерхности, чтобы поток вектора через боковую границу области пространства между двумя гиперповерхностями был равен 0. В классической теории поля таким свойством обладает, например, тензор энергии-импульса для электромагнитного поля. В вакууме лагранжиан поля не зависит явно от координат, поэтому имеется сохраняющаяся величина, ассоциируемая с потоком энергии-импульса.

Энергия из пустоты

Наука не даёт вразумительного определения ни полю, ни энергии. Зато она ясно формулирует — энергия не берётся из ниоткуда и никуда не девается. Пытаясь добывать «энергию из ничего», мы можем только стараться «встраиваться» в процесс её естественного преобразования из одних видов в другие.

Энергия определяется полезной работой, а поле — пространственными характеристиками влияния его источника. И статический электрический заряд, и динамический магнитный эффект вокруг проводника с током, и тепло нагретого тела считаются полями.

Любое поле может выполнить полезную работу, следовательно, передать часть своей энергии. Именно это свойство побуждает искать источники дармовой энергии в различных полях. Считается, что такой энергии существует в разы больше, чем в освоенных человечеством традиционных источниках.

Например, мы умеем использовать энергию гравитации огромной Земли, но не умеем её извлекать из притяжения малюсенького камня. Она слишком незначительная, чтобы это имело смысл, но практически неисчерпаема. Если придумать некий способ её извлечения из камешка, мы получим новый источник энергии.

Примерно этим занимаются исследователи и разработчики всех видов и мастей в попытках извлечь «энергию из ничего». То поле, из которого различные изыскатели стремятся научиться добывать энергетический ресурс, они называют эфир.

Эфир и его свойства

Этот термин бытовал в ходу у науки ещё столетие назад. Используя понятие «эфир», открыты были все базовые законы физики и не только. Оперируя именно этим понятием, проводили свои исследования и разработки Никола Тесла и другие умы XIX и начала XX века.

Наука однажды от эфира отреклась. В результате многие явления, такие как поля, оказались без него необъяснимы, а он сам теперь не имеет чёткого определения. Это не помешало использовать понятие «эфир» в обосновании разработок получения «свободной энергии из ничего». Хотя ныне под этим зачастую подразумеваются совершенно разные явления.

Сегодня под выражением «получить эфирную энергию» понимают как добычу её из того же эфира, который имел в виду Н. Тесла, так и вообще все способы получения «дармовой энергии из ничего». Эфир при этом считается структурной частью пространства и носителем любой энергии.

Никола Тесла и его идеи

Большинство современных конструкторов стремятся получить электричество именно «из воздуха». Самым известным разработчиком таких способов был Никола Тесла. Его называют первооткрывателем чуть ли не всех ныне существующих «благ цивилизации». Интернет, радио, телевидение, мобильная связь — практически всё считается основанным на открытых им ещё в начале XX века принципах.

Многие его разработки считаются утраченными ещё со времени его смерти. Одни из них известны исключительно как принципы, другие — всего лишь в общих чертах. Тем не менее, многие нынешние конструкторы пытаются сегодня воспроизвести открытия и устройства Тесла, пользуясь уже современными научными и технологическими открытиями.

Большинство идей Тесла базируются на извлечении её из полей, формируемых взаимодействием Земли со своей ионосферой. Эта система рассматривается как большой конденсатор, в котором одна пластина — Земля, а другая — её ионосфера, облучаемая космическими лучами. Как и любой конденсатор, такая система постоянно накапливает заряд.

https://youtube.com/watch?v=I5Ys4XBeB28

Ранние годы Эмми

Эмми была дочерью Макса Нётера, родилась и получила образование в Эрлангене. В 1900 году она получила сертификат на преподавание английского и французского языков в школах для девочек. Но захотела изучать математику в университете Эрлангена (ныне Университет Эрланген-Нюрнберг). В то время женщинам было позволено входить в аудиторию только с разрешения преподавателя. Она провела зиму 1903-04 гг., посещая лекции в университете Гёттингена, где преподавали математики Давид Гильберт, Феликс Клейн и Герман Минковский и астроном Карл Шварцшильд.

Она вернулась в Эрланген в 1904 году, когда там было разрешено женщинам быть полноправными студентами. Окончила этот университет. Она получила степень доктора философии в Эрлангене в 1907 году, защитив диссертацию об алгебраических инвариантах. Осталась в Эрлангене, где она работала без оплаты её собственных исследований и была ассистентом у отца, Макса Нётера.

В 1915 году Нётер был приглашена Гильбертом и Клейном в Гёттинген, считавшийся математической столицей мира. В 1916 г. переехала туда к ним. Вскоре, используя свои знания инвариантов, она помогала им исследовать математические аспекты недавно опубликованной Альбертом Эйнштейном общей теории относительности.

Будучи уже выдающимся математиком, Нетер как женщина не получила академической должности. Гильберт и Клейн убедили её остаться там, несмотря на яростные возражения некоторых членов профессорско-преподавательского состава против преподавания женщины в университете. До 1922 г. читала университетский курс алгебры вместо его официального руководителя Д. Гильберта (с его согласия).

В 1918 году Нётер обнаружила, что если лагранжиан (величина, характеризующая физическую систему, в механике это кинетическая минус потенциальная энергия) не изменяется, когда система координат изменяется, то есть величина, которая сохраняется. Например, когда лагранжиан зависит от изменения во времени, то энергия — сохраняемая величина. Это соотношение между тем, что известно как симметрии физической системы и её законами сохранения известно как теорема Нётер и оказалось ключевым результатом в теоретической физике.

Условия изменились при Веймарской республике, и Нётер получила официальный допуск к преподаванию в 1919 году. После долгого сопротивления университетского сообщества она была назначена «неофициальным» экстраординарным профессором Геттингенского университета. Этот статус не предоставлял академических прав и жалованья, но позволил создать группу учеников (их называли «мальчики Нетер»), из которой позднее вышли виднейшие алгебраисты. В 1920 году она опубликовала работы, сделавшие её одним из ведущих математиков.

В течение следующих шести лет ее исследования сосредоточены на общей теории идеалов (специальные подмножества колец), для которых её остаточная теорема — важная часть. На основе аксиоматики она разработала общую теорию идеалов для всех случаев. Её абстрактная теория помогла сблизить много важных математических разработок.

С 1927 научные интересы Нётер были сосредоточены на некоммутативных алгебрах (алгебры, в которых порядок перемножения чисел влияет на ответ), их линейных преобразований, и их применение к коммутативным числовым полям. Она построила теорию некоммутативных алгебр заново единой и чистой концептуально.

В сотрудничестве с Хельмутом Хассе и Рихардом Брауэром, она исследовала структуру некоммутативных алгебр и их применение к коммутативным полям с помощью перекрестного продукта (вид умножения, используется между двумя векторами). Важные работы этого периода: «Hyperkomplexe Grössen und Darstellungstheorie» (1929; «Гиперкомплексные системы счисления и их представление») и «Nichtkommutative Algebra» (1933; «Некоммутативная Алгебра»).

В дополнение к исследовательской и преподавательской работе, Нётер помогала отредактировать «Mathematische Annalen». С 1930 по 1933 год она была центром сильнейшей математической деятельности в Гёттингене.