Гиперкуб

Познание

Исследования с использованием виртуальной реальности показывают, что люди, несмотря на то, что живут в трехмерном мире, могут без специальной практики делать пространственные суждения о линейных сегментах, встроенных в четырехмерное пространство, на основе их длины (одномерного) и угла. (двухмерный) между ними. Исследователи отметили, что «участники нашего исследования имели минимальную практику в этих задачах, и остается открытым вопрос, можно ли получить более устойчивые, окончательные и богатые представления 4D с увеличенным опытом восприятия в виртуальных средах 4D». В другом исследовании была проверена способность людей ориентироваться в 2D, 3D и 4D лабиринтах. Каждый лабиринт состоял из четырех участков пути произвольной длины, соединенных случайными ортогональными поворотами, но без ответвлений или петель (т.е. фактически лабиринтов ). Графический интерфейс был основан на бесплатной игре Джона Макинтоша 4D Maze. Участники должны были пройти по тропе и, наконец, оценить линейное направление обратно к исходной точке. Исследователи обнаружили, что некоторые участники смогли мысленно интегрировать свой путь после некоторой практики в 4D (случаи более низкого измерения были для сравнения и для участников, чтобы изучить метод).

Можно ли представить четырёхмерное пространство и гиперкуб?

Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»

С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.

Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.

Геометрия

Геометрия четырехмерного пространства намного сложнее, чем у трехмерного пространства, из-за дополнительной степени свободы.

Так же, как в трех измерениях есть многогранники, состоящие из двухмерных многоугольников , в четырех измерениях есть 4-многогранники, состоящие из многогранников. В трех измерениях есть 5 правильных многогранников, известных как Платоновы тела . В четырех измерениях есть 6 выпуклых правильных 4-многогранников , аналогов Платоновых тел. Ослабление условий регулярности порождает еще 58 выпуклых однородных 4-многогранников , аналогичных 13 полурегулярным архимедовым телам в трех измерениях. Ослабление условий выпуклости порождает еще 10 невыпуклых правильных 4-многогранников.

Правильные многогранники в четырех измерениях (отображаются как ортогональные проекции в каждой плоскости симметрии Кокстера )

А 4 ,	В 4 ,	F 4 ,	H 4 ,
5-элементный{3,3,3}	тессеракт{4,3,3}	16 ячеек{3,3,4}	24-элементный{3,4,3}	600 ячеек{3,3,5}	120 ячеек{5,3,3}

В трех измерениях круг может быть выдавлен в виде цилиндра . В четырех измерениях есть несколько различных цилиндрических объектов. Сфера может быть экструдирована, чтобы получить сферический цилиндр (цилиндр со сферическими «крышками», известный как сфериндер ), а цилиндр может быть экструдирован для получения цилиндрической призмы (кубиндер). Декартово произведение двух окружностей может быть принято для получения duocylinder . Все трое могут «катиться» в четырехмерном пространстве, каждый со своими свойствами.

В трех измерениях кривые могут образовывать узлы, а поверхности — нет (если они не самопересекаются). Однако в четырех измерениях узлы, созданные с помощью кривых, можно тривиально развязать, смещая их в четвертом направлении, но 2D-поверхности могут образовывать нетривиальные, несамопересекающиеся узлы в четырехмерном пространстве. Поскольку эти поверхности двумерны, они могут образовывать гораздо более сложные узлы, чем струны в трехмерном пространстве. Бутылка Клейна является примером такой затруднительной поверхности. Другая такая поверхность — реальная проективная плоскость .

Гиперсфера

Стереографическая проекция из Clifford тора : множество точек (сов ( ), Sin ( ), соз ( б ), Sin ( б )), который представляет собой подмножество 3-мерной сферы .

Множество точек в евклидовом 4-пространстве , находящихся на одинаковом расстоянии R от фиксированной точки P _0, образует гиперповерхность, известную как 3-сфера . Гиперобъем закрытого пространства составляет:

Vзнак равно12π2р4{\ displaystyle \ mathbf {V} = {\ begin {matrix} {\ frac {1} {2}} \ end {matrix}} \ pi ^ {2} R ^ {4}}

Это часть метрики Фридмана – Лемэтра – Робертсона – Уокера в общей теории относительности, где R заменяется функцией R ( t ), где t означает космологический возраст Вселенной. Увеличение или уменьшение R со временем означает расширение или сжатие Вселенной, в зависимости от плотности массы внутри.

Ортогональность и словарный запас

В привычном трехмерном пространстве повседневной жизни есть три оси координат — обычно обозначается Икс, у, и z—С каждой осью ортогональный (т.е. перпендикулярно) двум другим. Шесть сторон света в этом пространстве можно назвать вверх, вниз, Восток, Запад, север, и юг. Позиции по этим осям можно назвать высота, долгота, и широта. Длины, измеренные по этим осям, можно назвать высота, ширина, и глубина.

Для сравнения, четырехмерное пространство имеет дополнительную координатную ось, ортогональную остальным трем, которая обычно обозначается ш. Чтобы описать два дополнительных основных направления, Чарльз Ховард Хинтон придумал термины ана и ката, от греческих слов, означающих «вверх по направлению» и «вниз от» соответственно. Позиция вдоль ш ось можно назвать верность, как придумано Генри Мор.

Как упоминалось выше, Герман Минковский использовал идею четырех измерений для обсуждения космологии, включая конечное скорость света. Добавляя временное измерение к трехмерному пространству, он указал альтернативную перпендикулярность, гиперболическая ортогональность. Это понятие придает его четырехмерному пространству модифицированную форму. одновременность соответствующий электромагнитным отношениям в его космосе. Мир Минковского преодолел проблемы, связанные с традиционными абсолютное пространство и время космология ранее использовалась во вселенной трех пространственных измерений и одного измерения времени.

Развёртки

Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом — нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).

Но не наглядна развёртка только для глаз. Как раз благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.

Элементы гиперкуба

Гиперкуб размерности n имеет 2n «сторон» (одномерная линия имеет 2 точки; двухмерный квадрат — 4 стороны; трехмерный куб — 6 граней; четырехмерный тессеракт — 8 ячеек). Количество вершин (точек) гиперкуба равно 2 n (например, для куба — 2 3 вершин).

Количество m-мерных гиперкубов на границе n-куба равно

Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.

Элементы гиперкубов

n-куб
Название
Вершина(0-грань)
Ребро(1-грань)
Грань(2-грань)
Ячейка(3-грань)
(4-грань)
(5-грань)
(6-грань)
(7-грань)
(8-грань)

0-куб
Точка
1

1-куб
Отрезок
2
1

2-куб
Квадрат
4
4
1

3-куб
Куб
8
12
6
1

4-куб
Тессеракт
16
32
24
8
1

5-куб
Пентеракт
32
80
80
40
10
1

6-куб
Хексеракт
64
192
240
160
60
12
1

7-куб
Хептеракт
128
448
672
560
280
84
14
1

8-куб
Октеракт
256
1024
1792
1792
1120
448
112
16
1

9-куб
Эненеракт
512
2304
4608
5376
4032
2016
672
144
18

Построение гиперкуба

Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.

1-мерный куб

В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.

Это одномерный куб.

2-мерный куб

У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.

Это куб в двумерном пространстве.

С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.

4-мерный куб (гиперкуб)

Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.

Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.

Визуализация многомерных кубов

Описание

Программа N-cube Model реализована на языке STATISTICA VISUAL BASIC и позволяет строить N-мерные кубы в среде STATISTICA.

Стандартный пакет включает в себя 3 файла: cube.svb, setup.svb, icon_cub.bmp. 

Программу можно либо интегрировать в систему STATISTICA через запуск и выполнение макроса setup.svb, либо просто использовать макрос cube.svb.

Если программа была проинсталлирована (через setup.svb) в систему STATISTICA, то ее можно запустить через панель инструментов в системе. Иначе можно просто запускать на выполнение макрос cube.svb. 

После запуска программы появится диалоговое окно. См. Рис. 1. 

 Можно задавать:

• размерность куба ( N ), от N = 3 до N = 7.

• выделять слой в кубе, помеченный кодами ( Active Cut Level ), указывается номер слоя от 0 до N+1. Если номер равен 0, то помечаются все уровни.

• строить куб пошагово с задержкой ( Active Time Delay ), задается в миллисекундах.

• также, при наличии открытой таблицы с данными, можно строить многомерный куб по данным в таблице. Размерность куба в этом случае разумнее установить равной количеству бинарных переменных в таблице. ( Count ActiveDataSet ).

После запуска приложения на экране диалоговое окно, в котором можно задать вышеперечисленные параметры для построения куба. См. Рис.9.

 Рис. 9. Диалоговое окно с параметрами многомерного куба.  

После нажатия на кнопку ОК, появится рисунок с моделью. См. Рис.10.

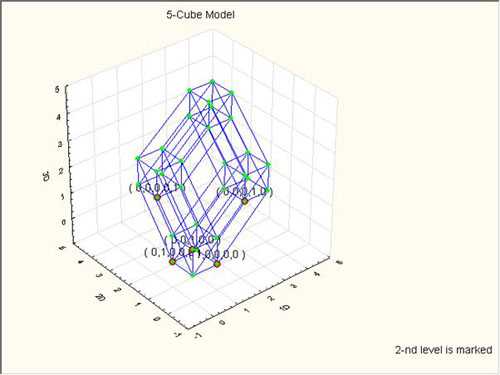
 Рис. 10. Пятимерный куб с помеченным 2-м слоем.  

Так как программа интегрирована в систему STATISTICA, то к полученному рисунку применимы все графические средства. Например, можно добавлять новые объекты через графическую панель, вращать график или использовать инструмент кисть, для отображения меток вершин в случае, когда была задана соответствующая опция. 

Программная реализация

Многомерный куб строится перебором всевозможных измерений (ребер), по которым вершина (0,0,…,0) переводится в (1,1,…,1). 

Любой такой путь (последовательность ребер и вершин) можно увидеть, если щелкнуть левой клавишей мышки по какому-либо ребру, которое принадлежит данному пути.

Программно путь представляется в виде последовательности бинарных кодов вершин, которые хранятся во внутренней таблице данных.

После формирования внутренней таблицы с бинарными кодами, начинается процесс визуализации данных многомерного куба. Последовательно перебираются все пути. Если установлена задержка ( Active Time Delay ), то программа будет «простаивать» между визуализацией соседних путей из таблицы.

Если установлена опция выделения слоя (Active Cut Level), то после визуализации всего куба, вершины, сумма кодов которых равна заданному уровню слоя, будут помечены красными метками с текстовыми значениями.

Если установлена опция просчета куба по таблице с данными (Count ActiveDataSet), то все автоматически включается опция пометить все вершины и дополнительно к текстовым меткам всех вершин добавляется число, соответствующее количеству элементов, удовлетворяющих коду данной вершины (см. пример с Titanic2.sta выше). 

Заключение

Итак, мы показали, как строить многомерные кубы в STATISTICA.

Такие диаграммы очень полезны в маркетинге, банковской сфере, промышленности, медицине — везде, где возникают многомерные данные и нужно найти способ их увидеть.

Что такое гиперкуб? Построение тессеракта

Виды гиперкубов и их названия 1. Точка — нулевое измерение 2. Отрезок — одномерное пространство 3. Квадрат — двумерное пространство (2D) 4. Куб — трёхмерное пространство (3D) 5. Тессеракт — четырёхмерное пространство (4D) 6. Пентеракт — пятимерное пространство (5D) 7. Хексеракт — шестимерное пространство (6D) 8. Хептеракт — семимерное пространство (7D) 9. Октеракт — восьмимерное пространство (8D) 10. Энтенеракт — девятимерное пространство (9D) 11. Декеракт — десятимерное пространство (10D)

Гиперкуб — это обобщающее название куба в производном числе измерений. Всего измерений десять, плюс точка (нулевое измерение).

Соответственно, существует одиннадцать видов гиперкуба. Рассмотрим построение тессеракта — гиперкуба четвертого измерения:

Для начала построим точку А (рис. 1):

Рис. 1 Точка

После, соединим ее с точкой В. Получим вектор АВ (рис. 2):

Рис. 2 Вектор

Построим вектор, параллельный вектору АВ, и назовем его CD. Соединив начала и концы векторов, получим квадрат ABDC (рис. 3):

Рис. 3 Квадрат

Теперь построим еще один квадрат A1B1D1C1, который лежит в параллельной плоскости. Соединив точки подобным образом, получим куб (рис. 4):

Рис. 4 Куб

У нас есть куб. Представьте, что положение куба в трехмерном пространстве с течением времени изменилось. Зафиксируем его новое местоположение (рис 5.):

Рис. 5 Измененное положение куба в пространстве

А теперь, мы проводим вектора, которые соединяют местоположение точек в прошлом и в настоящем. Получаем тессеракт (рис. 6):

Рис. 6 Тессеракт (построение)

Подобным образом строятся остальные гиперкубы, конечно же учитывается смысл пространства, в котором гиперкуб находится.

Тессеракт в искусстве

• У Эдвине А. «Новая Равнина Абботта», гиперкуб выступает рассказчиком.
• В одном эпизоде «Приключений Джимми Нейтрона» «мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы » (1963) Роберта Хайнлайна .
• Роберт Э. Хайнлайн упоминал гиперкубы, по крайней мере, в трёх научно-фантастических рассказах. В «Доме четырёх измерений» («Дом, который построил Тил», ) он описал дом, построенный как развёртка тессеракта, а затем вследствие землетрясения «сложившийся» в четвёртом измерении и ставший «реальным» тессерактом.
• В романе «Дорога славы » Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
• Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
• В романе Алекса Гарленда (), термин «тессеракт» используется для трёхмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой.
• Сюжет фильма «Куб 2: Гиперкуб » сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов.
• Телесериал «Андромеда » использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены, чтобы управлять пространством и временем .
• Картина «Распятие на кресте » (Corpus Hypercubus) Сальвадора Дали ().
• Комиксы «Nextwave comic book» изображают средство передвижения, включающее в себя 5 зон тессеракта.
• В альбоме Voivod Nothingface одна из композиций названа «В моём гиперкубе».
• В романе Энтони Пирса «Маршрут Куба» одна из орбитальных лун Международной ассоциации развития называется тессерактом, который был сжат в 3 измерения.
• В сериале «Школа „Чёрная дыра“ » в третьем сезоне есть серия «Тессеракт». Лукас нажимает на секретную кнопку и школа начинает «складываться как математический тессеракт».
• Термин «тессеракт» и производный от него термин «тессировать» встречается в повести Мадлен Л’Энгл «Складка времени».
• TesseracT название британской джент группы.
• В серии фильмов Кинематографическая вселенная Marvel Тессеракт — это ключевой элемент сюжета, космический артефакт в форме гиперкуба.
• В рассказе Роберта Шекли «Мисс Мышка и четвертое измерение» один писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
• В фильмах Первый Мститель, Мстители. Тессеракт-энергия все вселенной

Представление других измерений

От 2D к 3D

Ранняя попытка объяснить концепцию дополнительных измерений появилась в 1884 году с публикацией романа о плоской земле Эдвина А. Эббота «Флатландия: романтика множества измерений«.  Действие в романе разворачивается в плоском мире, называемом «Флатландия», а повествование ведется от лица жителя этого мира — квадрата. Однажды во сне квадрат оказывается в одномерном мире — Лайнландии, жители которой (треугольники и другие двумерные объекты представлены в виде линий) и пытается объяснить правителю этого мира существование 2-го измерения, однако, приходит к выводу о том, что его невозможно заставить выйти за рамки мышления и представления только прямых линий.

Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.

Сфера, с точки зрения Квадрата — Окружность. │ commons.wikimedia.org

Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.

Сфера пытается объяснить квадрату устройство трехмерного мира, но квадрат понимает только понятия «вверх/вниз» и «лево/право», он не способен постичь понятия «вперед/назад».

Непостижимая Квадратом тайна третьего измерения на примере прохождения сферы через плоскость. Герой наблюдает уменьшение Окружности до точки и её исчезновение. │ commons.wikimedia.org

Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.

Квадрат, вооруженный своим новым знанием, начинает осознавать возможность существования четвертого измерения. Также он приходит к мысли, что число пространственных измерений не может быть ограничено. Стремясь убедить сферу в этой возможности, квадрат использует ту же логику, что и сфера, аргументирующая существование трех измерений. Но теперь из них двоих становится «близорукой» сфера, которая не может понять этого и не принимает аргументы и доводы квадрата — так же, как большинство из нас «сфер» сегодня не принимают идею дополнительных измерений.

Читать книгу ОНЛАЙН Скачать книгу в формате PDF

От 3D к 4D

Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.

Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..

Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.

Проекции

На двумерное пространство

Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства . Кроме того, проектирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:

Третья картинка демонстрирует тессеракт в изометрии , относительно точки построения. Это представление представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.

На трёхмерное пространство

Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.

Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.

Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра , а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.

Стереопара

Стереопара тессеракта изображается как две проекции на трёхмерное пространство. Такое изображение тессеракта разрабатывалось с целью представить глубину, как четвёртое измерение. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопическая картина, воспроизводящая глубину тессеракта.

Развёртка тессеракта

Поверхность тессеракта может быть развёрнута в восемь кубов (аналогично тому, как поверхность куба может быть развёрнута в шесть квадратов). Существует 261 различная развёртка тессеракта . Развёртки тессеракта могут быть подсчитаны нанесением на граф соединённых углов.