Как привести дроби к наименьшему общему знаменателю

Нахождение числа по дроби

Чтобы найти всё число по его дроби, мы делили это число на числитель имеющейся дроби и полученный результат умножали на знаменатель имеющейся дроби.

Например, зная что  рулетки составляет 12 см, мы можем найти длину всей рулетки. Для этого 12 нужно разделить на 2, и полученный результат умножить на 3

12 : 2 = 6

6 × 3 = 18

Получили 18. Значит длина всей рулетки равна 18 см.

Но есть и второй вариант решения. Для нахождения длины всей рулетки, достаточно 12 разделить на дробь .  Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:

Поэтому можно взять на заметку следующее правило нахождения числа по дроби:

Чтобы найти число по дроби, нужно это число разделить на данную дробь.

Пример 2.    всего пути составляет 6 км. Найти длину всего пути.

Чтобы найти длину всего пути, достаточно 6 разделить на дробь

Получили ответ 15. Значит длина всего пути составляет 15 километров.

Правило приведения дробей к наименьшему общему знаменателю

Чаще всего при решении задач алгебры, геометрии, физики и т.п. принято обыкновенные дроби приводить к наименьшему общему знаменателю, а не к любому общему знаменателю.

Алгоритм
:

1. С помощью НОК знаменателей заданных дробей найти наименьший общий знаменатель.
2. 2.Вычислить дополнительный множитель для заданных дробей. Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число и будет дополнительным множителем данной дроби.
3. Умножить на найденный дополнительный множитель числитель и знаменатель каждой дроби.

Пример 6

Найти наименьший общий знаменатель дробей $\frac{4}{16}$ и $\frac{3}{22}$ и привести к нему обе дроби.

Решение.

Воспользуемся алгоритмом приведения дробей к наименьшему общему знаменателю.

Вычислим наименьшее общее кратное чисел $16$ и $22$:

Разложим знаменатели на простые множители: $16=2\cdot 2\cdot 2\cdot 2$, $22=2\cdot 11$.

$НОК(16, 22)=2\cdot 2\cdot 2\cdot 2\cdot 11=176$.

Вычислим дополнительные множители для каждой дроби:

$176\div 16=11$ – для дроби $\frac{4}{16}$;

$176\div 22=8$ – для дроби $\frac{3}{22}$.

Умножим числители и знаменатели дробей $\frac{4}{16}$ и $\frac{3}{22}$ на дополнительные множители $11$ и $8$ соответственно. Получим:

$\frac{4}{16}=\frac{4\cdot 11}{16\cdot 11}=\frac{44}{176}$

$\frac{3}{22}=\frac{3\cdot 8}{22\cdot 8}=\frac{24}{176}$

Обе дроби приведены к наименьшему общему знаменателю $176$.

Ответ: $\frac{4}{16}=\frac{44}{176}$, $\frac{3}{22}=\frac{24}{176}$.

Иногда для того, чтобы находить наименьший общий знаменатель, нужно провести ряд трудоемких вычислений, что может не оправдывать цель решения задачи. В таком случае можно воспользоваться наиболее простым способ – свести дроби к общему знаменателю, который представляет собой произведение знаменателей данных дробей.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Заметим, что 84: 21 = 4; 72: 12 = 6 . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Правильные и неправильные дроби

В самом начале своего пути при изучении дробей мы узнали, что правильная дробь — это та дробь, у которой числитель меньше знаменателя.

В школьной литературе можно встретить другое определение правильной дроби. Выглядит оно следующим образом:

Правильная дробь всегда меньше единицы.

Как понять данное определение? Дробь сама по себе указывает на то, что какой-либо объект разделен на несколько частей. И это всегда один единственный объект. Под единицей именно это и подразумевается.

Например, пусть у нас имеется одна пицца:

В данном случае она и является единицей.

Если мы отрежем от этой пиццы половину, то есть (одну вторую пиццы), то наш кусок будет меньше, чем вся целая пицца:

В этом и заключается суть фразы «правильная дробь всегда меньше единицы».

Наша половинка пиццы является дробью   и она меньше одной целой пиццы, то есть меньше единицы:

Это выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 0,5. А это рациональное число меньше единицы:

На координатной прямой можно увидеть, как располагаются эти числа:

Видно, что рациональное число 0,5 располагается левее, чем 1. А мы помним, что чем левее число располагается на координатной прямой, тем оно меньше.

С неправильными дробями всё было наоборот. Неправильной дробью мы назвали ту дробь, у которой числитель больше знаменателя.

Но в школьной литературе можно встретить другое определение неправильной дроби. Выглядит оно следующим образом:

Неправильная дробь всегда больше единицы или равна ей.

Например, рассмотрим неправильную дробь . Выделим в этой дроби целую часть, получим . Изобразим эту смешанную дробь в виде одной целой пиццы и ещё половинки пиццы:

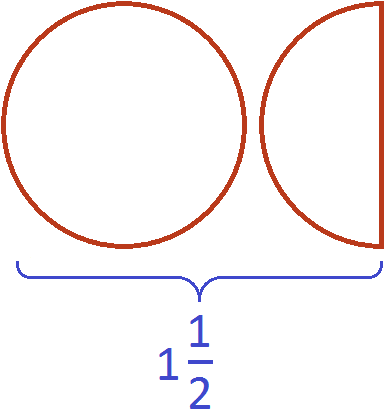
Вместе одна целая пицца и ещё половина пиццы больше, чем просто одна целая пицца

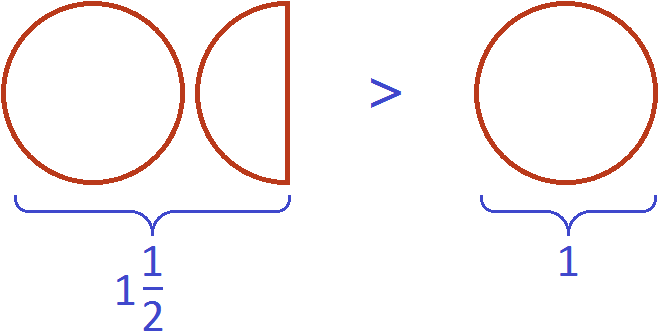
В этом и заключается суть фразы «неправильная дробь всегда больше единицы».

Одна целая пицца и ещё половина пиццы описывается смешанной дробью и эта смешанная дробь больше единицы:

Переведём смешанную дробь обратно в неправильную дробь, чтобы не противоречить правилу. Ведь речь в данном случае идёт о неправильных дробях:

что схематически будет выглядеть так:

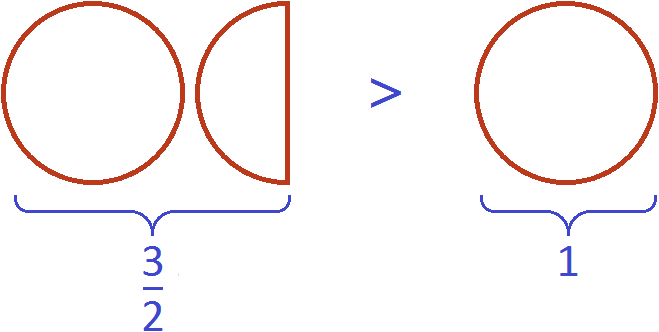
Выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 1,5. А это рациональное число больше единицы:

На координатной прямой можно увидеть, как располагаются эти числа:

Видно, что рациональное число 1,5 располагается правее, чем 1. А мы помним, что чем правее число располагается на координатной прямой, тем оно больше.

Неправильной также называется дробь равная единице. Речь в данном случае идет о тех дробях, у которых числитель и знаменатель равны.

Рассмотрим дробь . Изобразим её в виде двух одинаковых кусочков пиццы:

Фактически речь идёт не о дроби, а об одной целой пицце:

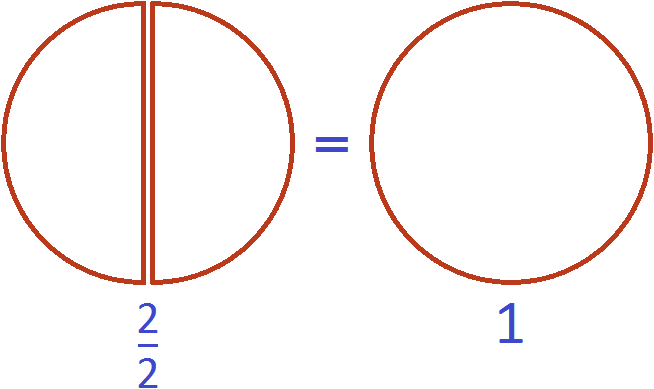
В этом и заключается суть фразы «неправильная дробь может равняться единице».

Любое целое число отличное от нуля (не равное нулю) можно представить в виде неправильной дроби со знаменателем 1. Например, числа 3, 5, 9, 12 можно представить в виде неправильных дробей со знаменателем 1

Представление объекта в виде единицы позволяет проще решать задачи. Рассмотрим примеры.

Пример 1. Куплен один шоколадный батончик. От него отрезали треть. Сколько батончика осталось?

Осталось две трети батончика. Сам батончик можно описать цифрой 1, далее из этой единицы вычесть треть:

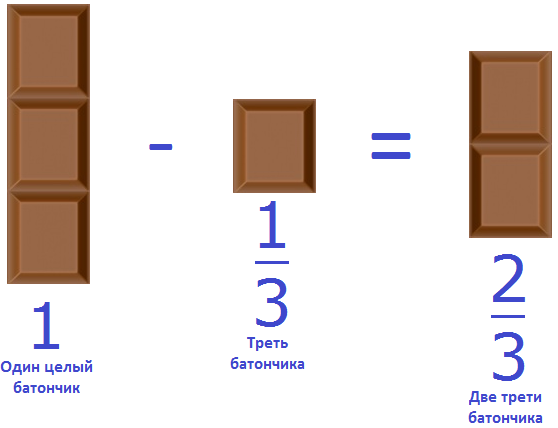
Не приводя на бумаге никаких вычислений, можно ответить на вопрос подобной задачи

Сказано «отрезали треть» — значит сразу нужно обратить внимание на то, что знаменатель равен 3

Если отрезали одну часть из трёх, то сколько частей должно остаться? Верно, две части. Поэтому и ответ «две части из трёх» или «две трети».

Пример 2. Куплен один пирог. От него отрезали две шестых. Сколько пирога осталось?

Осталось четыре шестых пирога. Сам пирог можно описать цифрой 1, далее из этой единицы вычесть две шестых:

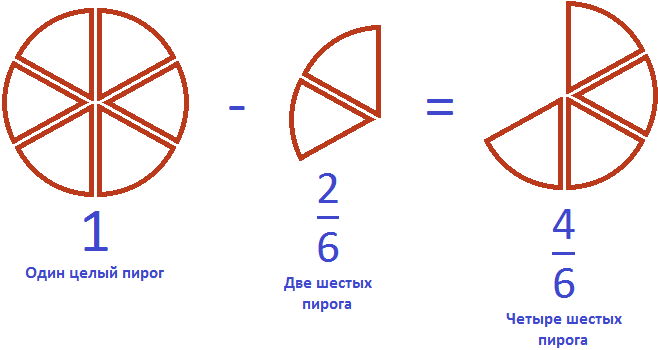
Как найти общий знаменатель дробей

Для того, чтобы найти общий знаменатель дробей, нужно найти наибольшее общее кратное знаменателей. Приведем пример, решим небольшое выражение:

$${3\over{5}}+{7\over{15}}$$

Найдем НОК знаменателей. Число 15 делится на число 5, значит

НОК(5,15)=15

$${3\over{5}}+{7\over{15}}={{3*3}\over{15}}+{7\over{15}}={9\over{15}}+{7\over{15}}={16\over{15}}=1 {1\over{15}}$$- обратите внимание, что при увеличении числителя, так же увеличился и знаменатель. В конце решения примера с дробями при возможности следует выделять целую часть выражения

Привести дроби к общему знаменателю можно только пользуясь основным свойством дроби. Формулировка этого свойства звучит так: если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится. Это значит, что при приведении дроби к общему знаменателю, требуется учитывать и увеличение числителя.

НОК можно найти аналитически, как мы это сделали в примере. Но чаще всего приходится прибегать к разложению на простые множители. Для того, чтобы найти НОК двух чисел следует:

• Разложить эти числа на простые множители
• Проверить, каких простых множителей не хватает в разложении.
• Берется число с наименьшим количеством множителей и к его разложению добавляют числа, которое есть в других разложениях, но отсутствуют в основном. При этом учитывается и количество чисел. Это значит, что если в основном разложении одно число 3, а в других разложениях два числа 3, то нужно домножить основное разложение на две тройки.

Что мы узнали?

Мы поговорили о приведении дробей к общему знаменателю. Рассказали, зачем это нужно, и какие операции с дробями можно выполнять без приведения к общему знаменателю. Привели пример и рассказали, как меняется числитель при приведении дробей к общему знаменателю.

1. /5

   Вопрос 1 из 5

   Знаменатель обозначает количество частей, на которое…

   • Разделили какой-то предмет
   • Количество частей, которое взяли для расчета
   • Количество частей яблока, которое было у Васи
   • Нет верного ответа

Как привести дроби к общему знаменателю, алгоритм

Чтобы осуществить операцию приведения, необходимо применить основное свойство дробей: если числитель и знаменатель дроби умножить на одно и то же число, отличное от нуля, дробь не изменится. То есть если подобрать правильные множители, то можно привести знаменатели к одному и тому же числу. Искомые множители называют дополнительными.

Это объяснение лежит в основе общего правила приведения дробей.

1. Найти общий знаменатель.
2. Для каждой дроби найти дополнительный множитель. Для этого необходимо разделить общий знаменатель на знаменатель каждой дроби.
3. Умножить обе части дроби на дополнительный множитель.

Существует несколько способов привести дроби к общему или наименьшему общему знаменателю.

Умножение «крест-накрест»

Самый простой способ — умножение «крест-накрест». Применяется следующий пошаговый алгоритм:

1. Умножить первую дробь на знаменатель второй дроби.
2. Умножить вторую дробь на знаменатель первой дроби.
3. При возможности — сократить получившиеся выражения.

\(\frac ab^{(d},\frac cd^{(b}=\frac{ad}{bd},\frac{cb}{bd}\)

Примечание

Недостаток этого метода — в размерах вычислений. При умножении могут получиться большие числа, которыми тяжело оперировать.

Метод общих делителей

Иногда один из знаменателей дроби уже делится на другой без остатка. В таком случае нет нужды перемножать их, количество действий сокращается.

1. Поделить больший знаменатель на меньший. Результат деления — это искомый дополнительный множитель.
2. Умножить дробь с меньшим знаменателем на дополнительный множитель. Другую дробь умножать ни на что не нужно.

\(\frac ab^{(x},\frac c{bx}=\frac{ax}{bx},\frac c{bx}\)

Этот метод хорош тем, что является более кратким вариантом умножения «крест-накрест». При этом его невозможно использовать при решении примеров, в которых числа в знаменателях не делятся друг на друга.

Метод наименьшего общего кратного

Суть приведения заключается в том, чтобы найти такое число, которое делится на каждый из знаменателей. К этому числу и необходимо привести знаменатели обеих дробей.

Определение

Наименьшее общее кратное (НОК) — это наименьшее число, на которое делится каждый из знаменателей. Обозначается он как НОК (a; b).

Пример

НОК (3; 4) = 12; НОК (8; 12) = 24.

Иногда найти НОК можно «на глаз», не выполняя дополнительных расчетов. К примеру, НОК (6; 9) = 18. Однако иногда на это может понадобиться больше времени. Описание примера таких вычислений приведено в примерах решения задач ниже.

Таким образом, основное преимущество это метода заключается в краткости вычислений. При этом его недостатком является сложность нахождения НОК в некоторых случаях.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2 . Это число намного меньше произведения 8 · 12 = 96 .

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Заметим, что 234 = 117 · 2; 351 = 117 · 3 . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4 . Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

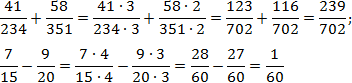
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!

Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.

Смешанная дробь

То, что у нас получилось (\( \displaystyle  5\frac{2}{3}\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

То, что между \( \displaystyle  5\) пирогами и \( \displaystyle  2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle  2x\)!!!

Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle  5\frac{2}{3}=5+\frac{2}{3}\).

Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.

Ты же знаешь, как это сделать?

Преобразование из смешанной дроби в неправильную дробь.

Конечно, нужно умножить знаменатель дроби (в случае с , \(\displaystyle5\frac{2}{3}\) знаменатель равен \( \displaystyle  3\)), умножить знаменатель…, верно, на \(\displaystyle5\) и прибавить нецелую часть, а именно – \( \displaystyle  2\) .

6 класс. Математика. Сложение и вычитание дробей с разными знаменателями. Сравнение дробей — Сложение и вычитание дробей с разными знаменателями. Сравнение дробей

Комментарии преподавателя

Вспом­ним, что мы уже знаем об обык­но­вен­ных дро­бях.

1. Любая дробь пред­став­ля­ет ко­ли­че­ство – часть от ка­ко­го-то числа. Эту часть мы умеем вы­чис­лять. На­при­мер,  от 100 – это .

2. Одну и ту же часть можно вы­ра­зить эк­ви­ва­лент­ны­ми дро­бя­ми (см. рис. 1). Эк­ви­ва­лент­ные дроби имеют раз­ную за­пись, од­на­ко вы­ра­жа­ют одно и то же ко­ли­че­ство, равны друг другу.

Рис. 1. При­мер эк­ви­ва­лент­ных дро­бей

3. При сло­же­нии/вы­чи­та­нии дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми скла­ды­ва­ем/вы­чи­та­ем чис­ли­те­ли.

4. При срав­не­нии двух дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми боль­шая та, у ко­то­рой чис­ли­тель боль­ше (см. рис. 2).

Рис. 2. При­мер срав­не­ния дро­бей с оди­на­ко­вым зна­ме­на­те­лем

Те­перь пе­рей­дем к во­про­су: что де­лать, если у дро­бей будут раз­ные зна­ме­на­те­ли. На­при­мер, как нам сло­жить  и  (см. рис. 3)?

Рис. 3. Ил­лю­стра­ция к при­ме­ру

Если мы за­ме­ним одну из дро­бей на эк­ви­ва­лент­ную, то их сумма, оче­вид­но, не из­ме­нит­ся.

Для дроби  су­ще­ству­ет бес­ко­неч­ное мно­же­ство дро­бей, ко­то­рые ей эк­ви­ва­лент­ны. Да­вай­те будем до­мно­жать чис­ли­тель и зна­ме­на­тель этой дроби на 2, 3, 4 и т.д. Тем самым мы по­лу­чим це­поч­ку эк­ви­ва­лент­ных дро­бей.

Ана­ло­гич­но по­сту­пим и со вто­рой дро­бью:

Мы можем за­ме­нить дробь эк­ви­ва­лент­ной. Нам нужно найти такие две дроби, у ко­то­рых зна­ме­на­тель оди­на­ко­вый, тогда мы смо­жем вы­пол­нить сло­же­ние. Оди­на­ко­вый зна­ме­на­тель у дро­бей  и , за­ме­ним ис­ход­ные дроби на них.

Рас­смот­рим еще несколь­ко при­ме­ров.

Необ­хо­ди­мо сло­жить дроби.

1) 

Ре­ше­ние

1) Неслож­но за­ме­тить, что дробь  легко пре­вра­ща­ет­ся в эк­ви­ва­лент­ную дробь со зна­ме­на­те­лем 4. Для этого нам нужно до­мно­жить ее чис­ли­тель и зна­ме­на­тель на 2.

Опре­де­ли­те раз­ность.

1)                                                2)                                                3) 

Ре­ше­ние

1) Неслож­но уви­деть, что мы вто­рую дробь может пре­вра­тить в дробь со зна­ме­на­те­лем 8, для этого умно­жим ее чис­ли­тель и зна­ме­на­тель на 2.

2) Обе дроби мы можем за­ме­нить эк­ви­ва­лент­ны­ми дро­бя­ми со зна­ме­на­те­лем 6. Чис­ли­тель и зна­ме­на­тель пер­вой дроби до­мно­жим на 3, а вто­рой – на 2.

3) Общим зна­ме­на­те­лем для этих дро­бей яв­ля­ет­ся число 30. По об­раз­цу ре­ша­ем по­след­ний при­мер.

Таким об­ра­зом, для сло­же­ния/вы­чи­та­ния двух дро­бей с раз­ны­ми зна­ме­на­те­ля­ми дроби необ­хо­ди­мо све­сти к об­ще­му зна­ме­на­те­лю.

Срав­ни­те дроби в при­ме­рах. Вы­пол­ни­те дей­ствия.

1)                                            2) 

Ре­ше­ние

1) Общий зна­ме­на­тель сла­га­е­мых дол­жен по­лу­чать­ся из чисел 15 и 18 умно­же­ни­ем на ка­кие-то числа. На­при­мер, зна­ме­на­тель 270 по­лу­ча­ет­ся при умно­же­нии 15 и 18 друг на друга, а зна­чит, может вы­сту­пать в ка­че­стве об­ще­го зна­ме­на­те­ля для ис­ход­ных дро­бей. Те­перь необ­хо­ди­мо умно­жить пер­вое сла­га­е­мое на 18, а вто­рое – на 15. По­лу­чен­ные дроби после умно­же­ния можно срав­нить:

Сле­до­ва­тель­но, пер&shy

Что такое дробь?

В 5 классе ученикам объясняют, что дробь это разделенное на кусочки целое. Причем знаменатель обозначает количество частей, на которое разделили какой-то предмет, а числитель количество этих частей, которое взяли для расчета.

Но в математике существует другое определение: дробью зовут незавершенную операцию деления. Это значит, что как любую дробь можно превратить в деление, так и любое деление можно превратить в дробь. Например:

$${5\over{7}}=5:7$$

$$7:13={7\over{13}}$$

$$12:9={12\over{9}}$$

Можно бесконечно приводить примеры, но смысл от этого не изменится: черта дроби заменяет знак деления.

Дроби — коротко о главном

Определения:

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.

Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.

Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle  \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).

Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).

Основное свойство дроби: 

Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).

Действия с дробями:

Сложение/вычитание дробей

• две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
• две обыкновенные дроби с разными знаменателями:
  • приводим дроби к наименьшему общему знаменателю;
  • складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
  • сокращаем полученную дробь
• две смешанные дроби с разными знаменателями: 
  • приводим дробные части этих чисел к наименьшему общему знаменателю;
  • по-отдельности складываем/вычитаем целые части и дробные части;
  • если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
  • сокращаем полученную дробь.

Умножение дробей

• умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
• умножение двух обыкновенных дробей: 
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь
• умножение двух смешанных чисел: 
  • преобразовываем смешанные дроби в неправильные;
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь;
  • если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

• деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
• деление натурального числа на дробь: число умножаем на дробь обратную данной
• деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
• деление двух смешанных чисел: 
  • преобразовываем смешанные дроби в неправильные;
  • умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).

Приведение дробей к наименьшему общему знаменателю

• найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
• разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
• умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).

Преобразования неправильной дроби в смешанную дробь

• поделите числитель дроби на ее знаменатель;
• остаток от деления запишите в числитель, знаменатель оставьте прежним;
• результат от деления запишите в качестве целой части.

Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).

Сравнение дробей:

• две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
• две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
• две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Десятичная точка в дробях

Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.

Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:

2.5 (две целых пять десятых)

15.65 (пятнадцать целых шестьдесят пять сотых)

Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.

Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.

Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.

Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.

Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».

Пример 1. Увеличить десятичную дробь 6,3 в десять раз.

Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.

Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.

Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63

На вопрос «как узнать на сколько цифр передвигать десятичную точку?», нужно смотреть во сколько увеличивается (или уменьшается) десятичная дробь. Если дробь нужно увеличить (или уменьшить) в десять раз, то десятичная точка сдвигается на одну цифру.

Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.

Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.

Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.

Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.

Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.

Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.

Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125

Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.

Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:

Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5

Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.

Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123

Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065

Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.