Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
2,1 : 10 = 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1 : 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Конечные десятичные дроби
До этого момента мы говорили лишь о десятичных дробях, в записи которых после десятичной запятой находится конечное число цифр. Такие дроби называют конечными десятичными дробями.
Определение.
Конечные десятичные дроби – это десятичные дроби, в записях которых содержится конечное число знаков (цифр).
Приведем несколько примеров конечных десятичных дробей: 0,317, 3,5, 51,1020304958, 230 032,45.
Любая конечная десятичная дробь может быть переведена в обыкновенную дробь или смешанное число (смотрите ). Например, конечной десятичной дроби 5,63 соответствует дробное число , а конечной десятичной дроби 0,2 отвечает правильная обыкновенная дробь 2/10 (или любая равная ей дробь, например, 1/5 или 10/50, смотрите ).
Однако не всякая обыкновенная дробь может быть представлена в виде конечной десятичной дроби. К примеру, дробь 5/13 не может быть заменена равной ей дробью с одним из знаменателей 10, 100, …, следовательно, не может быть переведена в конечную десятичную дробь. Подробнее об этом мы поговорим в разделе теории .
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
63 : 1 = 63
Значит значение выражения 6,3 : 0,1 равно 63
6,3 : 0,1 = 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
6,3 : 0,1 = 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
6,3 : 0,01 = 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3 : 0,001 = 6300
Десятичные дроби, определение, примеры десятичных дробей
Отталкиваясь от десятичной записи чисел, можно дать определение десятичных дробей.
Определение.
Десятичные дроби – это дробные числа, представленные в десятичной записи.
Озвученное определение позволяет привести примеры десятичных дробей: 152,21, 3,00762, 0,15, 0,00000003, 598 567 321,3500.
Возникает логичный вопрос: «Для чего нужны десятичные дроби»?
Например, десятичные дроби дают возможность более компактно записывать , знаменателями которых являются числа 10, 100, 1 000, …, и смешанные числа, знаменателями дробной части которых является числа 10, 100, 1 000, и т.д. К примеру, обыкновенной дроби 8/10 отвечает десятичная дробь 0,8, десятичной дроби 23/10 000 соответствует десятичная дробь 0,0023, смешанному числу соответствует десятичная дробь 512,03.
Отсюда вытекает следующий вопрос: «Как дробные числа со знаменателями 10, 100, … записываются в виде десятичных дробей»?
Ответом на него является информация из раздела .
Действия с десятичными числами

С дробями можно также выполнять и сравнения. Для этого используют алгебраические правила. Сложение дробей между собой осуществляют по правилу столбика. Это удобный метод, практически не позволяющий допускать ошибок. Согласно объяснению способа в математике, для сложения нужно записать два числа друг под другом так, чтобы их правые цифры были в одном столбике. Затем сложить цифры в нём, используя способ переноса десятков.
При сложении десятичных дробей происходит всё то же самое, но при этом нужно обязательно расположить выражения так, чтобы их запятые стояли чётко друг под другом. Сложение выполняют так, как и с натуральными числами, не учитывая запятые. После подсчёта запятую просто сносят вертикально вниз, отделяя целую часть от дольной.
При вычитании происходит всё аналогичным образом. При сложении и вычитании выполняют четыре пункта:
- Уравнивают количество знаков после запятой.
- Записывают дроби друг под другом так, чтобы запятые совпадали по вертикали.
- Складывают или вычитают по правилам арифметики.
- В полученном числе ставят запятую соответственно другим записям.

Для умножения дробей их записывают в столбик, а далее находят произведение, как и с обычными числами. Затем считают количество знаков после запятой первого умножаемого и умножителя и складывают их количество. Для получения ответа справа налево отсчитывают такое же количество знаков и после последнего ставят запятую. Умножаться могут любые дроби, исключений нет.
Чтобы разделить десятичную дробь, следует знать правило: если целая часть делимого меньше делителя, то в частном целых не будет. Деление выполняют по правилу того же столбика. Две части записывают через уголок и определяют неполное частное, сравнивая делимое с делителем. Далее выполняют действие, записывая цифру в частное. При записи под неполным частным правая его величина должна располагаться над правой цифрой произведения. После того как закончится деление целой части делимого, ставят запятую.
Слайды и текст этой презентации

История возникновения десятичных дробей

Зарождение десятичных дробей произошло в Китае Уже во II веке до н.э. там существовала десятичная система мер длины. Примерно в III веке н.э. десятичный счет распространился на меры массы и объема. Тогда и было создано понятие о десятичной дроби, сохранившей, однако метрологическую форму.В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Уже Лю Хуэй (III век), комментируя извлечение корней в « Математике в девяти книгах», рекомендовал пользоваться дробями со знаменателями 10, 100 и т.д.
Китай
Лю Хуэй


Узбекистан
ал-Каши
В XV веке, в Узбекистане, вблизи города Самарканда, который был тогда богатым культурным центром, жил математик и астроном, основатель астрономической обсерватории, ал-Каши. В 1427 году Ал-Каши написал книгу «Ключ к арифметике», в которой сформулировал основные правила действий с десятичными дробями, способы перевода шестидесятеричных дробей в десятичные и обратно. Целью ал-Каши было дать систему дробей, в которой все операции проводятся так же просто как с целыми числами, но которая основана на общеупотребительном десятичном основании. Десятичная дробь записывалась в одной строке с целой частью числа; для ее обозначения ал-Каши отделял дробь от целого вертикальной чертой или писал другим цветом или надписывал над цифрами названия разрядов, чаще всего называя только низший разряд, определяющий все остальные.


Франция
Франсуа Виет
В 1579 году десятичные дроби применяются в «Математическом каноне» французского математика Франсуа Виета (1540-1603), опубликованном в Париже. В этом сочинении, представляющем собой собрание тригонометрических таблиц, Виет решительно выступил в пользу употребления, как он выражался, тысячных и тысяч, сотых и сотен, десятых и десятков и т.д. взамен шестидесятеричной системы целых и дробей. При записи десятичных дробей Виет не придерживался какого-либо одного обозначения. Нередко он пишет как числитель, так и знаменатель, иногда отделяет цифры целой части от дробной вертикальной чертой, или же цифры целой части изображает жирным шрифтом, или, наконец, цифры дробной части дает более мелким шрифтом и подчеркивает.


Симон Стевин
Голландия
Широкое распространение десятичных дробей в Европе началось только после выхода в свет книги «Десятая» фламандского математика Симона Стевина (1548-1620). Его и считают изобретателем десятичных дробей. Стевин, уроженец Брюгге, вначале был купцом, затем во время Нидерландской революции инженером в войсках возглавлявшего республику Морица Оранского. «Астрологам , земледельцам, мерильщикам объемов, проверщикам емкостей бочек, стереометрам вообще, монетным мастерам и всему купечеству — Симона Стевина привет», — так обращается к своим читателям изобретатель десятичных дробей в своей книге «Десятая»(1585). Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. В книге он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании «изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов».

Стевин обозначает целые знаком 0, десятые – знаком 1, сотые – знаком 2 и т.д., причем цифры 0,1,2,. . . стоят над значащими цифрами или после них в кружках. Например, 5,13 Стевин обозначал
а 0,3752 обозначал


Иоганн Кеплер
Германия
Современную запись десятичных дробей т.е. отделение целой части запятой, предложил Иоганн Кеплер (1571 — 1630 гг.). В странах где говорят по -английски (Англия, США, Канада и др.), вместо запятой пишут точку.


В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого (1703г.)С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. Развитие техники, промышленности и торговли требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.
Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
3 − 1,2 = 1,8
Определение и понятие
История возникновения десятичных дробей тесно связана с учением о мерах. В Древнем Китае десятичную систему использовали для обозначения порядка. Полную теорию дробей в XV веке предложил узбекский астроном Джемшид Гиясэддин ал-Каши. Позже Стевин в своей книге «Десятая» начал записывать такие выражения в одну строку. Таким же образом их обозначал и Иоганн Кеплер. Используемая им запись осталась актуальной и сегодня.
Под дробью в математике понимают число, в состав которого входит одна или несколько равных долей единицы. Если стоит задача определить дробь конкретной величины, то её считают соответствующей единице. Например, пусть имеется круг, разделённый на шесть равных частей. Эти части называют долями. Всего их шесть, то есть каждая доля составляет шестую часть круга, исходную величину которого принимают как равную единице.
В математике это отношение обозначают в виде записи 1/6 и называют дробью. Читают его как «одна шестая». Любая дробь состоит из трёх элементов:
- Числителя — цифры или числа, стоящей в верхней части. Он показывает, сколько частей отобрано у целого, и является делимым.
- Знаменателя — числа, показывающего, на какое количество долей разделяют числитель.
- Дробной черты — разделяет числитель со знаменателем и фактически заменяет собой знак деления.
Краткая аннотация проекта
При работе над данным проектом рассматриваются предпосылки и история открытия десятичных дробей,что направленно на развитие познавательного интереса на уроках математики и приведёт к более осознанной работе по всей теме «Десятичные дроби».В проекте также рассматривается как записывать, сравнивать, складывать и вычитать десятичные дроби.Проводится аналогия со сложением и вычитанием натуральных чисел. Приведены примеры необходимости десятичных дробей в повседневной жизни.Материалы проекта могут использоваться в темах «Запись десятичных дробей», «Сложение и вычитание десятичных дробей».Выбранные мной цели и задачи обучения сформулированы, взяты из стандартов и поддерживаются основополагающим вопросом и вопросами учебной темы. Проект учитывает различные интересы учащихся и использует конкретные и качественно разработанные приемы.ИКТ в моем портфолио соответствуют возрасту учеников и учитывают их индивидуальные особенности.
Переход от обычных дробей к десятичным
Рассмотрим простую числовую дробь вида /. Можно воспользоваться основным свойством дроби и умножить числитель и знаменатель на такое число, чтобы внизу получилась степень десятки. Но прежде, чем это делать, прочитайте следующее:
Вот такие дела. Ну и как понять, приводится знаменатель к степени десятки или нет?
Ответ прост: разложите знаменатель на простые множители. Если в разложении присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 — что угодно), о степени десятки можно забыть.
Выпишем и разложим на множители знаменатели этих дробей:
20 = 4 · 5 = 22 · 5 — присутствуют только числа 2 и 5. Следовательно, дробь можно представить в виде десятичной.
12 = 4 · 3 = 22 · 3 — есть «запретный» множитель 3. Дробь не представима в виде десятичной.
640 = 8 · 8 · 10 = 23 · 23 · 2 · 5 = 27 · 5. Все в порядке: кроме чисел 2 и 5 ничего нет. Дробь представима в виде десятичной.
48 = 6 · 8 = 2 · 3 · 23 = 24 · 3. Снова «всплыл» множитель 3. Представить в виде десятичной дроби нельзя.
Итак, со знаменателем разобрались — теперь рассмотрим весь алгоритм перехода к десятичным дробям:
- Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
- Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
- Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.
Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом, чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.
И еще: если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную — и только затем применяйте описанный алгоритм.
Разложим на множители знаменатель первой дроби: 4 = 2 · 2 = 22. Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен 52 = 25. С ним количество двоек и пятерок сравняется. Имеем:
Теперь разберемся со второй дробью. Для этого заметим, что 24 = 3 · 8 = 3 · 23 — в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.
Две последних дроби имеют знаменатели 5 (простое число) и 20 = 4 · 5 = 22 · 5 соответственно — везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором — 5. Получаем:
![]()
Десятичные дроби — коротко о главном
1. Определение
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac{8}{10},\ \frac{13}{100},\frac{49}{1000}\));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac{1}{7}=0,\underbrace{142857}_{{период}}\underbrace{142857}_{период}142…=0,\left( 142857 \right)\))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac{3}{100}=0,03=0,030=0,030000\)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
- Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
- Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа
При умножении нам неважно, стоят ли запятые под запятыми и так далее
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
Чтение десятичных дробей
Скажем пару слов о правилах чтения десятичных дробей.
Десятичные дроби, которым соответствуют правильные обыкновенные дроби, читаются также как и эти обыкновенные дроби, только еще предварительно добавляется «ноль целых». Например, десятичной дроби 0,12 отвечает обыкновенная дробь 12/100 (читается «двенадцать сотых»), поэтому, 0,12 читается как «нуль целых двенадцать сотых».
Десятичные дроби, которым соответствуют смешанные числа, читаются абсолютно также как эти смешанные числа. Например, десятичной дроби 56,002 соответствует смешанное число , поэтому, десятичная дробь 56,002 читается как «пятьдесят шесть целых две тысячных».
Вопросы, направляющие проект
Когда и для чего возникли десятичные дроби?
-
Место и время появления десятичных дробей?
- Почему людям потребовалось новое число?
- Какие дроби можно записать в виде десятичной дроби?
- Как десятичную дробь записать в обыкновенном виде?
-
Родители: кто и когда придумал десятичные дроби?
- Кто же открыл десятичные дроби?
- Какая наука первая не смогла обойтись без десятичных дробей?
- Нужны ли в повседневной жизни десятичные дроби и если нужны,то где?
-
Как выглядели в детстве десятичные дроби?
- Как записывали самые первые десятичные дроби?
- Для чего служит запятая в записи десятичной дроби?
- Какие разряды в десятичных дробях?
- Десятичные дроби проще обыкновенных в применении?
- Чем сложение и вычитание десятичных дробей похоже на сложение и вычитание натуральных чисел?
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс преобразования десятичной дроби в обычный процент. Сформулируйте правило преобразования, состоящее из трех шагов. Как преобразовать десятичные дроби в дробные?
Правила преобразования десятичных дробей в дробные.
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение этого правила на примере.
Пример 8.Преобразование дробных дробей в десятичные дроби
Преобразуйте 3,025 в дробь.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
- В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
- Полученную дробь 3025 1000 можно сократить на 25, в результате чего мы получим: 3025 1000 = 121 40 .
Переведите десятичные дроби 0 и 0017 из десятичной системы счисления в обычную.
- В числителе запишем дробь 0, 0017, отбросив запятую и нули слева. Получится 17 .
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000. Данная дробь несократима.
Если в дробной дроби есть целое число, то дробь можно сразу преобразовать в смешанное число. Как это может произойти?
Давайте сформулируем другое правило.
Правило преобразования десятичной дроби в смешанное число.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Пример 10.Преобразование дробных дробей в смешанные числа
Пусть 155 и 06005 представлены в виде смешанных чисел.
- Записываем число 155, как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Возьмите смешанное число: 155,6005,100000.
Дробная часть может быть уменьшена на 5. Уменьшите его и получите конечный результат.
155, 06005 = 155 1201 20000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Рассмотрим пример дроби, преобразованной в повторяющуюся десятичную дробь. Прежде чем начать, давайте заявим, что каждая дробь может быть преобразована в обычную дробь.
В простейшем случае период дроби равен нулю. Дробь с нулевым периодом заменяется десятью десятичными знаками, и процесс преобразования таких дробей возвращается к преобразованию конечных дробей.
Пример 11.Преобразование дробных дробей в обычные дробные дроби
Преобразуйте периодическую дробь 3, 75 (0).
Используя нули справа, вы получите конечную десятичную дробь 3, 75.
Следуя алгоритму, описанному в предыдущем пункте, преобразуя эту дробь в обычную дробь, получаем
3, 75 (0) = 3, 75 = 375 100 = 15 4.
Что произойдет, если дробный период будет ненулевым? Периодические фракции следует рассматривать как сумму условий для сокращения геометрической прогрессии. Давайте проиллюстрируем это на примере.
Как читать десятичную дробь
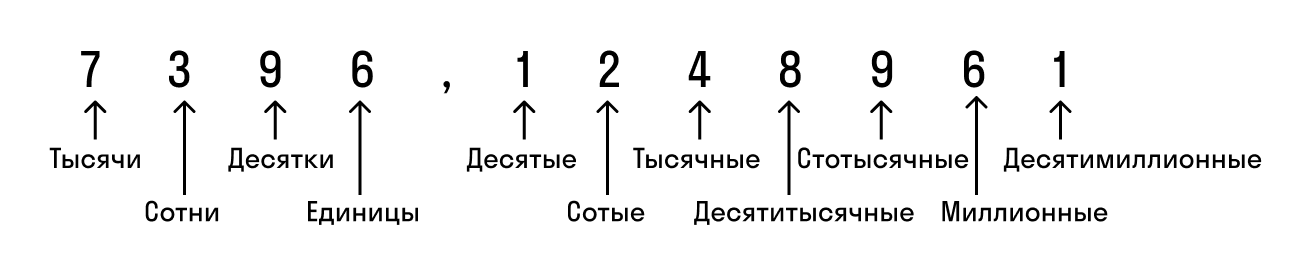
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Десятичные дроби на координатном луче
Между точками и десятичными дробями существует взаимно однозначное соответствие.
Разберемся, как строятся точки на координатном луче, соответствующие данной десятичной дроби.
Конечные десятичные дроби и бесконечные периодические десятичные дроби мы можем заменить равными им обыкновенными дробями, после чего построить соответствующие . Например, десятичной дроби 1,4 отвечает обыкновенная дробь 14/10, поэтому точка с координатой 1,4 удалена от начала отсчета в положительном направлении на 14 отрезков, равных десятой доле единичного отрезка.

Десятичные дроби можно отмечать на координатном луче, отталкиваясь от разложения данной десятичной дроби по разрядам. Например, пусть нам нужно построить точку с координатой 16,3007, так как 16,3007=16+0,3+0,0007, то в данную точку можно попасть, последовательно откладывая от начала координат 16 единичных отрезков, 3 отрезка, длина которых равна десятой доле единичного, и 7 отрезков, длина которого равна десятитысячной доле единичного отрезка.
Такой способ построения десятичных чисел на координатном луче позволяет сколь угодно близко приблизиться к точке, отвечающей бесконечной десятичной дроби.
Иногда возможно точно построить точку, соответствующую бесконечной десятичной дроби. Например, , тогда этой бесконечной десятичной дроби 1,41421… соответствует точка координатного луча, удаленная от начала координат на длину диагонали квадрата со стороной 1 единичный отрезок.
Обратный процесс получения десятичной дроби, соответствующей данной точке на координатном луче, представляет собой так называемое десятичное измерение отрезка. Разберемся, как оно проводится.
Пусть наша задача заключается в том, чтобы попасть из начала отсчета в данную точку координатной прямой (или бесконечно приблизиться к ней, если попасть в нее не получается). При десятичном измерении отрезка мы можем последовательно откладывать от начала отсчета любое количество единичных отрезков, далее отрезков, длина которых равна десятой доле единичного, затем отрезков, длина которых равна сотой доле единичного, и т.д. Записывая количество отложенных отрезков каждой длины, мы получим десятичную дробь, соответствующую данной точке на координатном луче.
К примеру, чтобы попасть в точку М на приведенном выше рисунке, нужно отложить 1 единичный отрезок и 4 отрезка, длина которых равна десятой доле единичного. Таким образом, точке М соответствует десятичная дробь 1,4.
Понятно, что точкам координатного луча, в которые невозможно попасть в процессе десятичного измерения, соответствуют бесконечные десятичные дроби.
Список литературы.
- Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
- Математика. 6 класс : учеб. для общеобразоват. учреждений / . — 22-е изд., испр. — М.: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.