Множества. операции над множествами.отображение множеств. мощность множества

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

1) Пересечение множеств характеризуется логической связкой И и обозначается значком

Пересечением множеств  и  называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:
Так, например, для множеств :

Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший .

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

Объединением множеств  и  называется множество , каждый элемент которого принадлежит множеству  или множеству :

Запишем объединение множеств : – грубо говоря, тут нужно перечислить все элементы множеств  и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если  , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

3) Разностью множеств  и  называют множество , каждый элемент которого принадлежит множеству  и не принадлежит множеству :
Разность  читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества . Чтобы записать разность , нужно из множества  «выбросить» все элементы, которые есть во множестве :

Пример с числовыми множествами: – здесь из множества целых чисел исключены все натуральные, да и сама запись  так и читается: «множество целых чисел без множества натуральных».

Зеркально: разностью множеств  и  называют множество , каждый элемент которого принадлежит множеству  и не принадлежит множеству :
Для тех же множеств  – из множества  «выброшено» то, что есть во множестве .

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется

Кроме того, иногда рассматривают симметрическую разность , которая объединяет оба «полумесяца»: – иными словами, это «всё, кроме пересечения множеств».

4) Декартовым (прямым) произведением множеств  и  называется множество  всех упорядоченных пар , в которых элемент , а элемент

Запишем декартово произведение множеств : – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества  последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества  присоединяем каждый элемент множества , затем к 3-му элементу множества  присоединяем каждый элемент множества »:

Зеркально: декартовым произведением множеств  и  называется множество  всех упорядоченных пар , в которых . В нашем примере: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы:

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары. А теперь гвоздь программы: декартово произведение  – это есть не что иное, как множество точек  нашей родной декартовой системы координат

А теперь гвоздь программы: декартово произведение  – это есть не что иное, как множество точек  нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

1) ;
2)

Множество  удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

3)

Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству , а  «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж

Краткое решение задачи в конце урока.

Отображение множеств

Отображение множества  во множество – это правило, по которому каждому элементу множества  ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой  – она ставит в соответствие каждому элементу  единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество  студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

 Векторы  Матрицы  Определители Комплексные числа (о, да!)  Теория пределов Что такое производная?

Установленное (добровольно или принудительно =)) правило  ставит в соответствие каждому студенту  множества  единственную тему реферата  множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества  образуют область определения функции (обозначается через ), а элементы множества  – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству  добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена –  одна из тем останется невостребованной.

Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)

Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .

Задумаемся, что это такое? Это правило , которое каждому элементу  области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:

Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Далее взглянем на старую знакомую параболу  . Здесь правило  каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной  – это правило , которое каждому значению независимой переменной  из области определения ставит в соответствие одно и только одно значение .

Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции  каждому «иксу» области определения  соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:  

А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при  или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

Другие способы построения

Существуют и другие способы построения системы вещественных чисел:

• теория бесконечных десятичных дробей. Действительными числами называются бесконечные десятичные дроби, среди которых периодические дроби составляют множество рациональных чисел, а непериодические дроби – иррациональные числа. Такой способ выгоден тем, что он является конструктивным и, кроме того, в наибольшей степени соответствует интуитивному понятию действительного числа. Этот способ изложен, например, в книге Ильина и Позняка.
• теория сечений в области рациональных чисел Дедекинда. Сечением в множестве рациональных чисел называется всякое разбиение совокупности всех рациональных чисел на два непустых класса — нижний и верхний, так что каждое число из нижнего класса строго меньше всякого числа из верхнего. Если в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества. В этом случае по определению полагают, что данное сечение определяет некоторое иррациональное число, которое находится между нижним и верхним классами, и тем самым производит данное сечение. Иначе говоря, для всякого сечения, не производимого никаким рациональным числом, вводят новый объект — иррациональное число, которое по определению больше всякого числа из нижнего класса и меньше всякого числа из верхнего класса.
• теория фундаментальных последовательностей Кантора. Вещественное число рассматривается как предел последовательности рациональных чисел. Последовательности, удовлетворяющие условию Коши, называются фундаментальными.

Во всех этих подходах в результате мы получаем некоторое множество объектов (вещественных чисел), обладающих определёнными свойствами: их можно складывать, умножать, сравнивать между собой. Более того, коль скоро установлены свойства этих объектов, мы можем больше не апеллировать к тем конкретным конструкциям, с помощью которых они были построены.

В математике важна не конкретная природа объектов, а лишь математические соотношения, существующие между ними.

Существуют и другие способы аксиоматизации вещественных чисел. Например, вместо аксиомы непрерывности можно использовать любое другое эквивалентное ей условие, или группу условий. Например, в системе аксиом, предложенной Гильбертом, используются следующие два условия:

• Аксиома Архимеда
• Аксиома полноты (в смысле Гильберта)

Таким образом, можно дать следующее эквивалентное определение: Множество вещественных чисел есть максимальное архимедово упорядоченное поле.

В качестве другого примера аксиоматизации вещественных чисел можно привести аксиоматику Тарского, состоящую всего из 8 аксиом.

Мощность множества

Интуиция подсказывает, что термин характеризует размер множества, а именно количество его элементов. И интуиция нас не обманывает!

Мощность пустого множества равна нулю.

Мощность множества  равна шести.

Мощность множества букв русского алфавита  равна тридцати трём.

И вообще – мощность любого конечного множества равно количеству элементов данного множества.

…возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. Что называется, и китайцы когда-нибудь закончатся.

Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью. Равномощность определяется следующим образом:

Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.

Множество  студентов равномощно множеству  тем рефератов, множество  букв русского алфавита равномощно любому множеству из 33 элементов и т.д. Заметьте, что именно любому множеству из 33 элементов – в данном случае имеет значение лишь их количество. Буквы русского алфавита можно сопоставить не только с множеством номеров 1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.

Гораздо более интересно обстоят дела с бесконечными множествами. Бесконечности тоже бывают разными! …зелёными и красными Самые «маленькие» бесконечные множества – это счётные множества. Если совсем просто, элементы такого множества можно пронумеровать. Эталонный пример – это множество натуральных чисел . Да – оно бесконечно, однако у каждого его элемента в ПРИНЦИПЕ есть номер.

Примеров очень много. В частности, счётным является множество всех чётных натуральных чисел . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:
Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество  счётно. Парадоксально, но с точки зрения мощности – чётных натуральных чисел столько же, сколько и натуральных!

Множество целых чисел тоже счётно. Его элементы можно занумеровать, например, так:

Более того, счётно и множество рациональных чисел . Поскольку числитель – это целое число (а их, как только что показано, можно пронумеровать), а знаменатель – натуральное число, то рано или поздно мы «доберёмся» до любой рациональной дроби  и присвоим ей номер.

А вот множество действительных чисел  уже несчётно, т.е. его элементы пронумеровать невозможно. Данный факт хоть и очевиден, однако строго доказывается в теории множеств. Мощность множества действительных чисел также называют континуумом, и по сравнению со счётными множествами это «более бесконечное» множество.

Поскольку между множеством  и числовой прямой существует взаимно-однозначное соответствие (см. выше), то множество точек числовой прямой тоже несчётно. И более того, что на километровом, что на миллиметровом отрезке – точек столько же! Классический пример: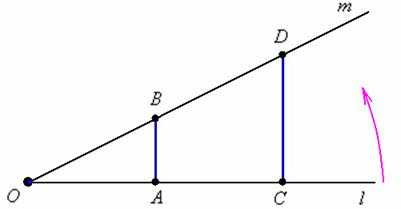
Поворачивая луч  против часовой стрелки до его совмещения с лучом  мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке  столько же точек, сколько и на отрезке и !

Данный парадокс, видимо, связан с загадкой бесконечности… но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди основы математической логики, а не философия =)

Спасибо за внимание и успехов вам в учёбе!

Решение заданий:

Задание 1

1)

2)  – это множество нечётных натуральных чисел:

3)

 – все точки  координатной плоскости
, удовлетворяющие двум указанным неравенствам. Аналогично:

Задание 2 Взаимно-однозначные функции на иллюстрациях урока Функции и графики:

(Переход на главную страницу)

Аксиома — непрерывность

Аксиома непрерывности, известная под названием аксиомы Дедекинда, формулируется так: если точки прямой разделены на два класса, то существуют пограничные точки, производящие это разделение и принадлежащие к одному из классов.
 

Аксиома непрерывности постулирует тот факт, что бесконечное множество точек ъ пространстве не имеет пустот. На числовой модели это значит, что координаты точек выражаются действительными числами.
 

Аксиома непрерывности выполняется в силу аксиомы Дедекинда для вещественных чисел.
 

Аксиома непрерывности, которая утверждает, что имеется набор точек, образующих границу ( кривую безразличия), которая разделяет расположенные в товарном пространстве ( commodity space) комбинации товаров на предпочтительные и непредпочтительные.
 

Вторая аксиома непрерывности называется аксиомой линейной полноты ( точки прямой линии образуют такую систему точек, которую нельзя дополнить новыми точками без нарушения ранее установленных аксиом) и лежит в основе взаимнооднозначного соответствия между множеством точек на числовой прямой и множеством вещественных чисел.
 

Из аксиомы непрерывности следует расширенная аксиома сложения.
 

Что касается аксиомы непрерывности, то она, очевидно, выполняется, так как сводится к аксиоме непрерывности для евклидовой прямой относительно следования пар.
 

Далее следует сформулировать аксиому непрерывности: относительно единичного отрезка ОЕ каждой точке Р соответствует в качестве абсциссы некоторое действительное число и наоборот.
 

Группа IV содержит две аксиомы непрерывности.
 

Группа IV содержит две аксиомы непрерывности.
 

Наконец, что касается аксиом непрерывности, то я укажу здесь только, как изображаются комплексные точки, лежащие как угодно близко к какой-нибудь действительной точке.
 

Из расширенной аксиомы сложения следует аксиома непрерывности.
 

Напротив, для бесконечных полей аксиома непрерывности V является независимой от аксиом I — IV. Так как новая аксиома существенна лишь для бесконечных полей вероятностей, то является почти невозможным разъяснить ее эмпирическое значение, например, так, как это было вкратце проделано для аксиом 1 — IV в § 2 главы первой. При описания какого-либо действительно наблюдаемого случайного процесса можно получать только конечные поля вероятностей. Бесконечные ноля вероятностей появляются только как идеализированные схемы действительных случайных явлений. Мы произвольно ограничиваемся при этом такими схемами, которые удовлетворяют аксиоме V. Это ограничение оказывается целесообразным в самых различных исследованиях.
 

Напротив, для бесконечных полей аксиома непрерывности V является независимой от аксиом I — IV-Так как новая аксиома существенна лишь для бесконечных полей вероятностей, то является почти невозможным разъяснить ее эмпирическое значение, например, так, как это было вкратце проделано для аксиом I — IV в § 2 главы первой. При описания какого-либо действительно наблюдаемого случайного процесса можно получать только конечные поля вероятностей. Бесконечные поля вероятностей появляются только как идеализированные схемы действительных случайных явлений.
 

Наконец, результат Ленсберга использует аксиому непрерывности ФКВ в дополнение к сепарабельности. При этом дополнительном требовании вне рассмотрения остаются любые оптимальные по Парето переопределения эгалитарного метода ( такие, как максимизация лексиминного ПКБ), которые удовлетворяют свойству сепарабельности.
 

Окрестность точки

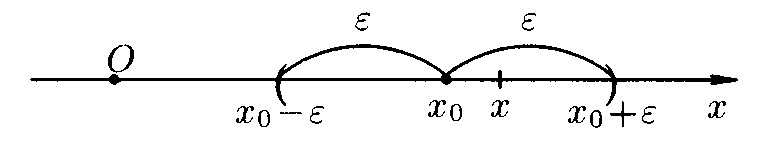
Рис. 2. Окресность точки

Любой интервал %%(a, b)%%, содержащий некоторую точку %%x_0%% называют окрестностью этой точки и обозначают %%\text{U}(x_0)%%, т.е. %%\text{U}(x_0) = (a, b)%%, если %%x_0 \in (a, b)%%. Точку %%x_0%%, расположенную в середине своей окрестности %%(a, b)%%, в этом случае именуют центром окрестности, а расстояние %%\varepsilon = \frac{(b — a)}{2}%% — радиусом окрестности. Тогда множество %%\{x: |x — x_0| < \varepsilon\}%% называют %%\varepsilon%%-окрестностъю точки %%x_0%% и обозначают %%\text{U}(x_0, \varepsilon)%% или %%\text{U}_\varepsilon(x_0)%% (рис. 2).

На расширенной числовой прямой вводят понятие окрестности и для бесконечных точек %%+\infty%% и %%—\infty%%, тем самым уравнивая эти точки с конечными при рассмотрении многих вопросов. Пусть %%M%% — некоторое положительное число. Тогда %%\text{U}(+\infty) = \{x \in \mathbb{R}: x > M\}%% и %%\text{U}(-\infty) = \{x \in \mathbb{R}: x < -M\}%%, а для объединения бесконечных точек %%\text{U}(\infty) = \{x \in \mathbb{R}: |x| > M\}%%. Ясно, что для любой из бесконечных точек окрестность с меньшим значением %%M%% включает окрестность с большим значением %%M%%.

Абсолютное значение

Абсолютным значением (или модулем) %%|a|%% любого действительного числа %%a%% называют действительное число, удовлетворяющее условиям:
$$
|a| = \begin{cases}
a, \text{ если } a \geq 0 \\
-a, \text{ если } a < 0
\end{cases} ~~~~~~~~~~(1)
$$

Отсюда следует, что абсолютное значение любого действительного числа неотрицательно %%(|a| \geq 0)%%, а также
$$
\begin{array}{l}
|a| = |-a|, \\
|a| \geq a, \\
|a| \geq -a, \\
-|a| \leq a \leq |a|.
\end{array}~~~~~~~~~~(2)
$$

Геометрически %%|a|%% соответствует расстоянию между точками числовой прямой, изображающими числа %%0%% и %%a%%.

Пусть справедливо неравенство %%|a| < \varepsilon%%, где %%\varepsilon%% — некоторое
положительное число (%%\varepsilon > 0%%). Тогда это неравенство равносильно двойному неравенству
$$
-\varepsilon < a < \varepsilon.
$$
Равносильность рассмотренных неравенств будет сохранена, если строгие неравенства (%%<%%) заменить на нестрогие (%%\leq%%): %%|a| \leq \varepsilon%% равносильно %%-\varepsilon \leq a \leq \varepsilon%%.

Для любых действительных чисел %%a%% и %%b%% справедливо равенство
$$
|ab| = |a||b| ~~~~~~~~~~(3)
$$
и выполняются неравенства:
$$
\begin{array}{lr}
|a + b| \leq |a| + |b| &~~~~~~~~~~(4),\\
|a — b| \geq \big||a| — |b|\big|&~~~~~~~~~~(5).
\end{array}
$$

При помощи (1) и (2) докажем неравенство (4): если %%a + b \geq 0%%, то
$$
|a + b| = a + b \leq |a| + |b|
$$
а если %%a + b < 0%%, то
$$
|a + b| = -(a + b) = (-a) + (-b) < |a| + |b|
$$

Приведенные выше свойства полностью описывают множество всех действительных чисел.

Множество всех действительных чисел, а также множество точек числовой прямой обычно обозначают %%\mathbb R%%.

История становления понятия вещественного числа

Наивная теория вещественных чисел

Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом.

Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса дошла до нас в изложении Евклида («Начала», книга V). По существу, теория Евдокса — это геометрическая модель вещественных чисел. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Классическая теория Дедекинда для построения вещественных чисел по своим принципам чрезвычайно похожа на изложение Евдокса. Однако модель Евдокса неполна во многих отношениях, например, не содержит аксиомы непрерывности, не даёт общей теории арифметических операций для величин или их отношений и др.

Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным». После гибели античной науки на передний план выдвинулись математики Индии и стран ислама, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе, где поначалу разделяли рациональные и иррациональные (буквально: «неразумные») числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века), который провозгласил:
Шаблон:Цитата
Он же, с некоторыми оговорками, легализовал отрицательные числа, а также развил теорию и символику десятичных дробей, которые с этого момента начинают вытеснять неудобные шестидесятеричные.

Спустя столетие Ньютон в своей «Универсальной арифметике» (1707 года) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону:
Шаблон:Цитата
Долгое время это прикладное определение считалось достаточным, так что практически важные свойства вещественных чисел и функций не доказывались, а считались интуитивно очевидными (из геометрических или кинематических соображений). Например, считался самоочевидным тот факт, что непрерывная кривая, точки которой расположены по разные стороны от некоторой прямой, пересекает эту прямую. Строгое определение понятия непрерывности также отсутствовало. Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.

Даже после того, как Коши разработал достаточно строгий фундамент анализа, положение не изменилось, поскольку теории вещественных чисел, на которую обязан был опираться анализ, не существовало. Из-за этого Коши сделал немало ошибок, положившись на интуицию там, где она приводила к неверным выводам: например, он полагал, что сумма ряда из непрерывных функций всегда непрерывна.

Создание строгой теории

Первую попытку заполнить пробел в основаниях математики сделал Бернард Больцано в своей статье «Чисто аналитическое доказательство теоремы, что между любыми двумя значениями, дающими результаты противоположного знака, лежит по меньшей мере один действительный корень уравнения» (1817 год). В этой пионерской работе ещё нет целостной системы вещественных чисел, но уже приводится современное определение непрерывности и показывается, что на этой основе теорема, упомянутая в заглавии, может быть строго доказана. В более поздней работе Больцано даёт набросок общей теории вещественных чисел, по идеям близкой к канторовской теории множеств, но эта его работа осталась неопубликованной при жизни автора и увидела свет только в 1851 году. Взгляды Больцано значительно опередили своё время и не привлекли внимания математической общественности.

Современная теория вещественных чисел была построена во второй половине XIX века, в первую очередь трудами Вейерштрасса, Дедекинда и Кантора. Они предложили различные, но эквивалентные подходы к теории этой важнейшей математической структуры и окончательно отделили это понятие от геометрии и механики.

Примечания[ | код]

1. Зорич, В. А. Математический анализ. Часть I. — Изд. 4-е, испр.. — М.: «МЦНМО», 2002. — С. 43.

2. Например, при аксиоматическом определении действительного числа принцип непрерывности Дедекинда входит в число аксиом, а при конструктивном определении действительного числа с помощью дедекиндовых сечений то же самое утверждение уже является теоремой — см. например
   Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002. — Т. 1. — 416 с. — ISBN 5-9221-0196-X.

3. Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 38.

4. Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 84.

5. Зорич, В. А. Математический анализ. Часть I. — Изд. 4-е, испр.. — М.: «МЦНМО», 2002. — С. 81.

Архимедово свойство

Каково бы ни было число %%a%%, существует такое целое число %%n \in \mathbb{N}%%, что %%n > a%%.

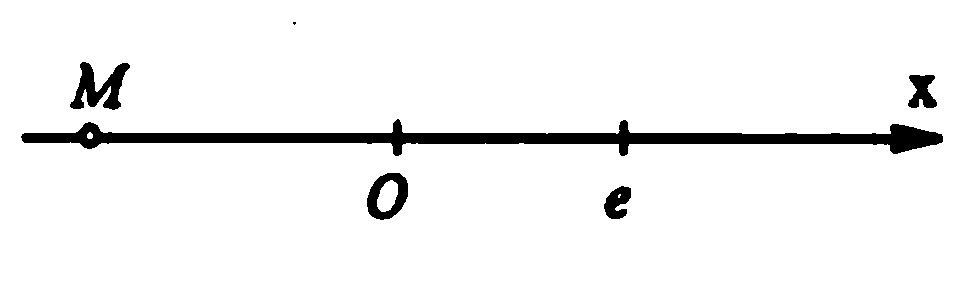
Рис. 1. Числовая прямая

Прежде чем сформулировать следующее свойство действительных чисел, напомним, что на прямой задана система отсчета, если на этой прямой фиксированы две различные точки (точки %%O%% и %%e%% на рис. 1). Левую из них (точку %%O%%) называют началом отсчета, а длина отрезка %%Oe%% задает единицу масштаба. Прямую с заданной системой отсчета называют координатной осью. Ее обычно обозначают %%Ox%%. Точка %%O%% делит координатную ось на две части: положительную полуось, где лежит точка %%e%%, и отрицательную полуось.

Координатой точки %%M%% на оси %%Ox%% называют длину отрезка %%OM%%, взятую со знаком %%+%%, если точка %%M%% лежит на положительной полуоси, и со знаком %%-%%, если точка %%M%% лежит на отрицательной полуоси.

Очевидно, что каждой точке %%M%% на оси %%Ox%% соответствует действительное число %%x%%, а именно, ее координата. И обратно, каждому действительному числу на оси %%Ox%% соответствует
точка, для которой это действительное число является ее координатой. Всякий раз, когда это потребуется, будем считать, что между действительными числами и точками некоторой прямой установлено такого рода соответствие, причем %%e = 1%%, %%O = 0%%.

Таким образом, совокупность всех действительных чисел можно рассматривать как числовую прямую. Иногда вместо числовой прямой используют также термин «вещественная прямая». Отождествление действительных чисел с точками на числовой прямой будет в дальнейшем чрезвычайно полезным, так как служит вспомогательным средством для понимания и мотивацией введения новых понятий.

Подмножество %%X%% множества действительных чисел называют промежутком, если вместе с любыми двумя числами %%x_1, x_2%% это подмножество содержит любое %%x%%, заключенное между ними. Используют промежутки следующих видов:

• %%(a, b) = \{x: a < x < b\}%% — интервал, или открытый промежуток;
• %% = \{x: a \leq x \leq b\}%% — отрезок, или замкнутый промежуток (иногда используют термин «сегмент»);

• %%(a, b] = \{x: a < x \leq b\}%% и %%[a, b) = \{x: a \leq x < b\}%% — полуинтервалы.

Если %% \supseteq %%, то отрезок %%%% называют вложенным в отрезок %%%%.

Аксиомы поля

Множество, на котором определены 2 операции, которые удовлетворяют следующим свойствам, называется полем.

• На множестве должно быть определено отображение — операция сложения, сопоставляющее каждой упорядоченной паре элементов из множества некоторый элемент из того же множества, называемый суммой.
• Также, на множестве должно быть определено отображение — операция умножения, сопоставляющее каждой упорядоченной паре элементов из множества некоторый элемент, называемый произведением.

При этом имеют место следующие свойства.

• Коммутативность сложения $a+b=b+a$ для любых $a, b$ из множества.
• Ассоциативность сложения $(a+b)+c=a+(b+c)$

• Существование нуля. Существует элемент 0 из этого множества, называемый нулём, такой, что для любого $a$ из множества $a+0 = a$

• Существование противоположного элемента. Для любого $a$ существует элемент $-a$, называемый противоположным к $a$, такой что $a+(-a) = 0$
• Коммутативность умножения $a \cdot b=b \cdot a$
• Ассоциативность умножения $(a \cdot b) \cdot c=a \cdot (b \cdot c)$

• Существование единицы. Существует элемент множества 1, называемый единицей, такой, что для любого $a$ из множества $a \cdot 1 = a$

• Существование обратного элемента. Для любого $a$ не равного нулю, существует элемент $a^{-1}$, обозначаемый также $\frac{1}{a}$ и называемый обратным к $a$, такой, что $a \cdot a^{-1} = 1$
• Дистрибутивный закон умножения относительно сложения $a \cdot (b+c) = a \cdot b+a \cdot c$
• Нетривиальность поля. Единица и ноль — различные элементы множества: $1 \ne 0$