Гравитационная постоянная: определение, формула, единицы измерения, опыт кавендиша

К закону о всемирном тяготении

Ньютон продолжил размышления. Поскольку Земля притягивает Луну, то и она сама должна притягиваться к Солнцу. Причем сила такого притяжения тоже должна подчиняться описанному им закону. А потом Ньютон распространил его на все тела вселенной. Поэтому и название закона включает слово «всемирное».

Силы всемирного тяготения тел определяются как пропорционально зависящие от произведения масс и обратные квадрату расстояния. Позже, когда был определен коэффициент, формула закона приобрела такой вид:

F т = G (m 1 *х m 2) : r 2 .

В ней введены такие обозначения:

Формула гравитационной постоянной вытекает из этого закона:

G = (F т Х r 2) : (m 1 х m 2).

Определение

В соответствии с законом Ньютона всемирного тяготения , притяжения силы ( F ) между двумя точечными телами прямо пропорциональна произведению их масс ( м ₁ и м ₂ ) и обратно пропорционально квадрату расстояния , г , между их центры масс .:

Fзнак равнограммм1м2р2.{\ displaystyle F = G {\ frac {m_ {1} m_ {2}} {r ^ {2}}} \ ,.}

Константа пропорциональности , G , гравитационная постоянная. В просторечии гравитационная постоянная также называется «Большой G», в отличие от «малого g» ( g ), которое является локальным гравитационным полем Земли (эквивалентным ускорению свободного падения). Где M _⊕ — масса Земли, а r _⊕ — радиус Земли , эти две величины связаны соотношением:

g =GM _⊕г _⊕2.

Гравитационная постоянная появляется в поле Эйнштейна уравнений в общей теории относительности ,

граммμν+Λграммμνзнак равноκТμν,{\ Displaystyle G _ {\ mu \ nu} + \ Lambda g _ {\ mu \ nu} = \ kappa T _ {\ mu \ nu} \ ,,}

где G _μν — тензор Эйнштейна , Λ — космологическая постоянная , g _μν — метрический тензор , T _μν — тензор энергии-импульса , а κ — константа, первоначально введенная Эйнштейном, которая напрямую связана с ньютоновской постоянной гравитации:

κзнак равно8πграммc2{\ Displaystyle \ каппа = {\ гидроразрыва {8 \ pi G} {с ^ {2}}}} ≈ 1,866 × 10 −26 м⋅кг −1 .

Задачи, в которых требуется знание гравитационной постоянной

Задача первая

Условие. Чему равно ускорение свободного падения на одной из планет Солнечной системы, например, на Марсе? Известно, что его масса 6,23·1023 кг, а радиус планеты 3,38·106 м.

Решение. Нужно воспользоваться той формулой, которая была записана для Земли. Только подставить в нее значения, данные в задаче. Получится, что ускорение свободного падения будет равно произведению 6,67 х 10-11 и 6,23 х 1023, которое потом нужно разделить на квадрат 3,38·106. В числителе получается значение 41,55 х 1012. А в знаменателе будет 11,42 х 1012. Степени сократятся, поэтому для ответа достаточно только узнать частное двух чисел.

Ответ: 3,64 м/с2.

Задача вторая

Условие. Что нужно сделать с телами, чтобы уменьшить их силу притяжения в 100 раз?

Решение. Поскольку массу тел изменять нельзя, то сила будет уменьшаться за счет удаления их друг от друга. Сотня получается от возведения в квадрат 10. Значит, расстояние между ними должно стать в 10 раз больше.

Ответ: отдалить их на расстояние, превышающее изначальное в 10 раз.

Измерение гравитационной постоянной

Наиболее раннее упоминание гравитационной постоянной, как отдельной константы, определяющей гравитационное взаимодействие, найдено в «Трактате по механике», написанном в 1811-м году французским физиком и математиком — Симеоном Дени Пуассоном.

Измерение гравитационной постоянной проводится различными группами ученых и по сей день. При этом, несмотря на обилие доступных исследователям технологий, результаты экспериментов дают различные значения данной константы. Из этого можно было бы сделать вывод, что, возможно, гравитационная постоянная на самом деле непостоянная, а способна менять свое значение, с течением времени или от места к месту. Однако, если значения константы по результатам экспериментов разнятся, то неизменность этих значений в рамках этих экспериментов уже проверена с точностью до 10-17. Кроме того, согласно астрономическим данным постоянная G не изменилась в значительной степени за несколько последних сотен миллионов лет. Если постоянная Ньютона и способна меняться, то ее изменение не превысило б отклонение на число 10-11 – 10-12 в год.

Примечательно, что летом 2014-го года совместно группа итальянских и нидерландских физиков провели эксперимент по измерению гравитационной постоянной совсем иного вида. В эксперименте использовались атомные интерферометры, которые позволяют отследить влияние земной гравитации на атомы. Значение константы, полученное таким образом, имеет погрешность 0,015% и равняется G = 6.67191(99) × 10−11 м3·с−2·кг−1.

Уменьшение силы притяжения тел с их отдалением

Для начала он выдвинул предположение о том, что сила тяжести убывает. И ее значение находится в обратной зависимости от расстояния, возведенного в квадрат. Причем это расстояние нужно отсчитывать от центра планеты. И провел теоретические расчеты.

Потом этот ученый воспользовался данными астрономов о движении естественного спутника Земли — Луны. Ньютон рассчитал, с каким ускорением она вращается вокруг планеты, и получил те же результаты. Это свидетельствовало о правдивости его рассуждений и позволило сформулировать закон всемирного тяготения. Гравитационная постоянная в его формуле пока отсутствовала

На этом этапе было важно определить зависимость. Что и было сделано

Сила тяжести уменьшается обратно пропорционально расстоянию от центра планеты, возведенному в квадрат.

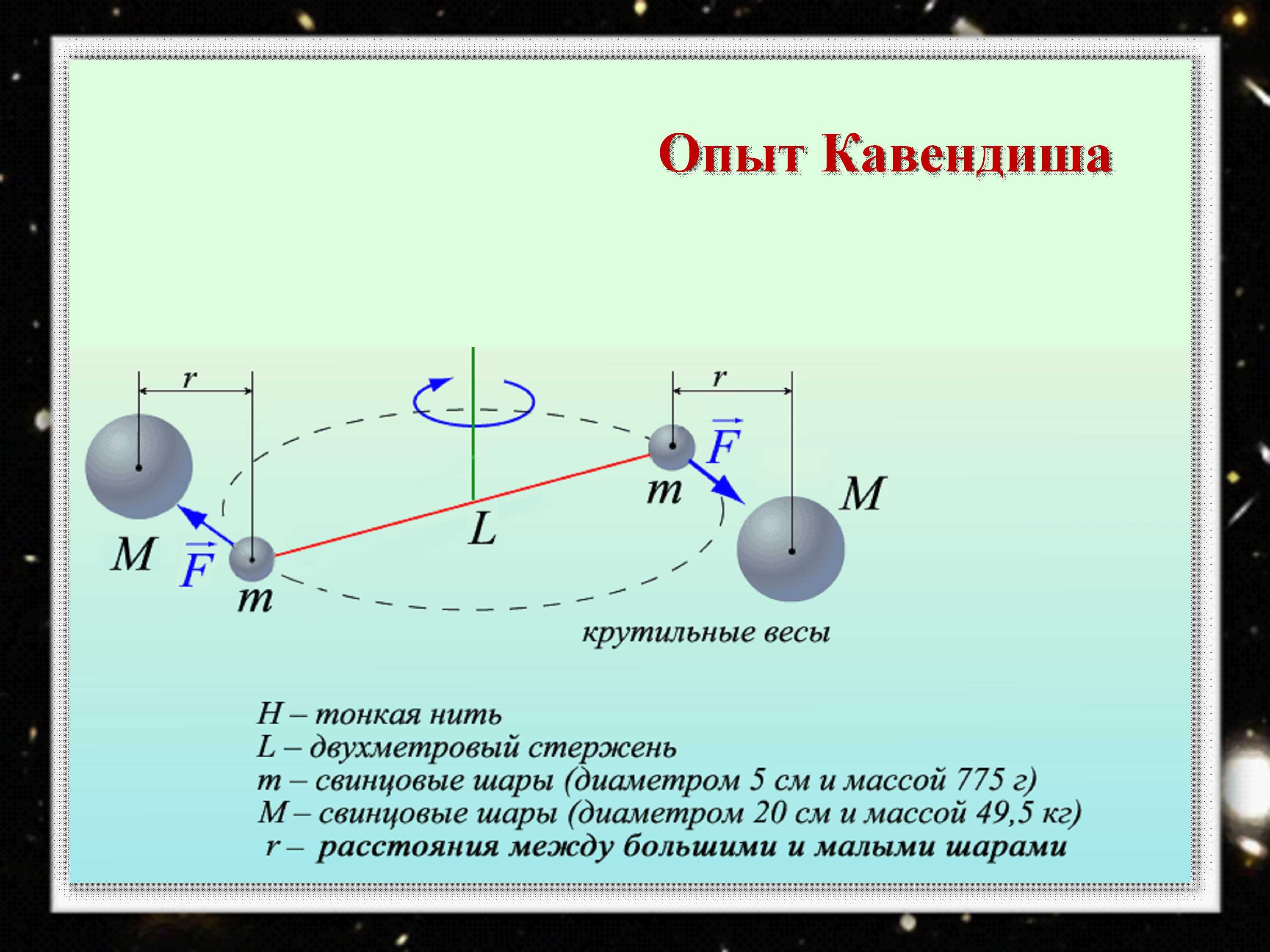
Эксперимент Кавендиша

Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».

Генри Кавендиш (1731 — 1810)

Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.

Установка Генри Кавендиша

Более наглядное описание эксперимента доступно в видео ниже:

https://www.youtube.com/watch?v=iOgrSlzyFMA» frameborder=»0″ allowfullscreen>

Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли. Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила.

Третий закон Ньютона

F₁ — сила, с которой первое тело действует на второе

F₂ — сила, с которой второе тело действует на первое

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

Материалы по теме

Гравитационные волны

Значение

Гравитационная постоянная — это константа пропорциональности гравитационной силе (то есть притяжения между телами), последняя подчиняется закону обратных квадратов расстояний и пропорциональна произведению масс и .
грамм{\ displaystyle G}м1{\ displaystyle m_ {1}}м2{\ displaystyle m_ {2}}

Ценность в международной системе

грамм{\ displaystyle G} соответствует силе между двумя массами в один килограмм каждая, на расстоянии одного метра.

В 2018 году CODATA рекомендует следующее значение в единицах СИ :

граммзнак равно6,67430(15)×10-11м3kграмм-1s-2{\ displaystyle G = 6 {,} 674 \, 30 (15) \ times 10 ^ {- 11} \; {\ rm {m ^ {3} \, kg ^ {- 1} \, s ^ { — 2}}}}

где число в скобках — это стандартная неопределенность последних объясненных цифр, то есть:

σграммзнак равно0,00015×10-11м3kграмм-1s-2{\ displaystyle \ sigma _ {G} = 0 {,} 000 \, 15 \ times 10 ^ {- 11} \; {\ rm {m ^ {3} \, кг ^ {- 1} \, s ^ {-2}}}},

либо относительная неопределенность:

σграммграммзнак равно2,2×10-5{\ displaystyle {\ frac {\ sigma _ {G}} {G}} = 2 {,} 2 \ times 10 ^ {- 5}}, или с точностью до 22 частей на миллион.

Производная единица м 3 кг -1 с -2 также может быть записана в Н м 2 кг -2 .

Значение в системе CGS

В системе CGS значение константы:

граммзнак равно(6,67430±0,00015)×10-8противм3грамм-1s-2{\ displaystyle G = (6 {,} 674 \, 30 \ pm 0 {,} 000 \, 15) \ times 10 ^ {- 8} \; {\ rm {cm ^ {3} \, g ^ {- 1} \, s ^ {- 2}}}}.

Стоимость в натуральных единицах

В так называемых « естественных » единицах и другие физические константы, такие как скорость света, имеют значение 1.
грамм{\ Displaystyle G \,} против{\ displaystyle c \,}

Получены новые значения

Согласно отчету Erland Myles Standish (в) до Международного астрономического союза в 1994 году, наилучшая оценка величины G был:

граммзнак равно6,67259(30)×10-8противм3 грамм-1 s-2{\ Displaystyle G = 6 {,} 672 \, 59 (30) \ times 10 ^ {- 8} \; {\ rm {cm ^ {3} \ g ^ {- 1} \ s ^ {- 2}} }}

В 2007 году JB Fixler, GT Foster, JM McGuirk и MA Kasevich получили следующий рейтинг:

граммзнак равно6,693(72)×10-11м3 kграмм-1 s-2{\ displaystyle G = 6 {,} 693 (72) \ times 10 ^ {- 11} \; {\ rm {m ^ {3} \ kg ^ {- 1} \ s ^ {- 2}}}}

В исследовании, проведенном в 2010 году, Гарольд В. Паркс и Джеймс Э. Фаллер получили значение, отличное от уже найденного:

граммзнак равно6,67234(14)×10-11м3 kграмм-1 s-2{\ Displaystyle G = 6 {,} 672 \, 34 (14) \ times 10 ^ {- 11} \; {\ rm {m ^ {3} \ kg ^ {- 1} \ s ^ {- 2}} }}

В 2014 году CODATA рекомендовала следующее значение (теперь заменено значением CODATA 2018) в единицах СИ :

граммзнак равно6,67408(31 год)×10-11м3 kграмм-1 s-2{\ Displaystyle G = 6 {,} 674 \, 08 (31) \ times 10 ^ {- 11} \; {\ rm {m ^ {3} \ kg ^ {- 1} \ s ^ {- 2}} }}

пусть будет относительная неопределенность .
σграммграммзнак равно4,6×10-5{\ displaystyle {\ frac {\ sigma _ {G}} {G}} = 4 {,} 6 \ times 10 ^ {- 5}}

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

формула закона всемирного тяготения

G – коэффициент пропорциональности или гравитационная постоянная;

m_1,m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

значение гравитационной постоянной

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

гравитационная постоянная в законе всемирного тяготения

ФИЗИКА

Физический смысл гравитационной постоянной

Из формулы (3.2.8) находим

Отсюда следует, что если расстояние между телами численно равно единице (R = 1 м) и массы взаимодействующих тел тоже равны единице (m₁ = m₂ = 1 кг), то гравитационная постоянная численно равна модулю силы . Таким образом, гравитационная постоянная численно равна модулю силы тяготения, действующей на тело массой 1 кг со стороны другого тела такой же массы при расстоянии между телами, равном 1 м.

Из формулы (3.3.1) также видно, что в СИ гравитационная постоянная выражается в .

Опыт Кавендиша

Значение гравитационной постоянной G может быть найдено только опытным путем. Для этого, как видно из формулы (3.3.1), надо измерить модуль силы тяготения , действующей на тело массой m₁ со стороны тела массой m₂ при известном расстоянии R между телами.

Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1798 г. с помощью прибора, называемого крутильными весами. Схематично крутильные весы показаны на рисунке 3.8. Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Для этой проволоки предварительно определялись силы упругости, возникающие в ней при закручивании на различные углы. Два больших свинцовых шара (диаметром 20 см и массой 49,5 кг) можно было близко подводить к маленьким шарам. Силы притяжения со стороны больших шаров заставляли маленькие шары перемещаться к ним, при этом натянутая проволока немного закручивалась. Степень закручивания была мерой силы, действующей между шарами. Угол закручивания проволоки (или поворота стержня с малыми шарами) оказался столь малым, что его пришлось измерять с помощью оптической трубы. Результат, полученный Кавендишем, только на 1% отличается от значения гравитационной постоянной, принятого сегодня:

Таким образом, силы притяжения двух тел массой по 1 кг каждое, находящихся на расстоянии 1 м друг от друга, по модулям равны всего лишь 6,67 • 10-11 Н. Это очень малая сила. Только в том случае, когда взаимодействуют тела огромной массы (или по крайней мере масса одного из тел велика), сила тяготения становится большой. Например, Земля притягивает Луну с силой F = 2 • 1020 Н.

Гравитационные силы — самые «слабые» из всех сил природы. Это связано с тем, что гравитационная постоянная мала. Но при больших массах космических тел силы всемирного тяготения становятся очень большими. Эти силы удерживают все планеты возле Солнца.

Ускорение свободного падения

В условиях нашей планеты, мы привыкли оперировать понятие силы тяжести – силы, что действует на объект со стороны планеты.

Сила тяжести выводится из закона всемирного притяжения путем замены величин, не зависящих от массы тела, на одну величину – ускорение свободного падения.

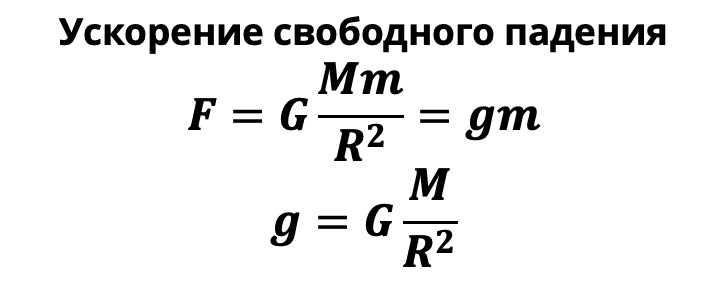
Таким образом, вместо использования многих значений: массы планеты, ее радиуса и гравитационной константы, можно использовать одно.

Чем отличается вес и масса

Эти два понятия перепутались в повседневной жизни и часто заменяют одно другое. Но вес и масса – это две совершенно разных величины.

Масса – это то, сколько килограммов «есть» в теле. Это его характеристика, которая зависит только от свойств самого объекта.

А вес – это сила, с которой объект давит на опору. На горизонтальных поверхностях он равен силе тяжести, на наклонных чуть меньше, но тоже зависит от силы тяжести.

Именно из-за маленькой силы притяжения, космонавты на Луне могли так высоко подпрыгивать, ведь их вес стал значительно меньше, а их масса осталась неизменной.

В чем физический смысл этого числа?

Если в формулу, которая дана для закона всемирного тяготения, подставить конкретные числа, то получится интересный результат. В частном случае, когда массы тел равны 1 килограмму, а расположены они на расстоянии 1 метра, сила тяготения оказывается равной самому числу, которое известно для гравитационной постоянной.

То есть смысл гравитационной постоянной заключается в том, что она показывает, с какой силой будут притягиваться такие тела на расстоянии одного метра. По числу видно, насколько мала эта сила. Ведь она в десять миллиардов меньше единицы. Ее даже невозможно заметить. Даже при увеличении тел в сотню раз результат существенно не изменится. Он по-прежнему останется гораздо меньше единицы. Поэтому становится понятно, отчего сила притяжения заметна только в тех ситуациях, если хотя бы одно тело имеет огромную массу. Например, планета или звезда.

Общие сведения

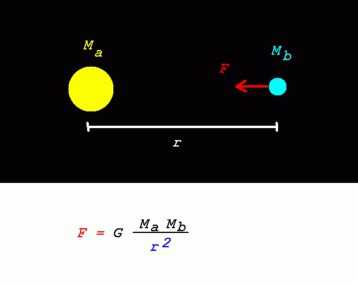
Гравитационная постоянная или иначе – постоянная Ньютона – одна из основных констант, используемых в астрофизике. Фундаментальная физическая постоянная определяет силу гравитационного взаимодействия. Как известно, силу, с которой каждое из двух тел, взаимодействующих посредством гравитации, притягивается можно высчитать из современной формы записи закона всемирного тяготения Ньютона:

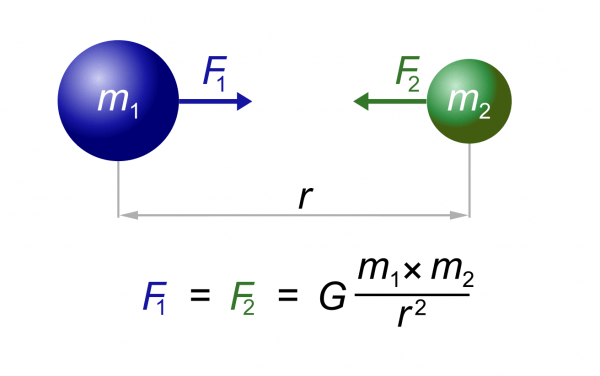
Гравитационное взаимодействие двух тел

Здесь:

m1 и m2 — тела, взаимодействующие посредством гравитации
F1 и F2 – векторы силы гравитационного притяжения, направленные к противоположному телу
r – расстояние между телами
G – гравитационная постоянная

Данный коэффициент пропорциональности равен модулю силы тяготения первого тела, которая действует на точечное второе тело единичной массы, при единичном расстоянии между этими телами.

G = 6,67408(31)·10−11 м3·с−2·кг−1, или Н·м²·кг−2.

Очевидно, что данная формула широко применима в области астрофизики и позволяет рассчитать гравитационное возмущение двух массивных космических тел, для определения дальнейшего их поведения.

Связанные константы

Стандартный гравитационный параметр

Произведение называется стандартным гравитационным параметром и обозначается ( мю ).
граммM{\ displaystyle GM}μ{\ displaystyle \ mu}

Этот параметр обеспечивает практическое упрощение различных формул, связанных с гравитацией.

В зависимости от того, обозначает ли масса Земли или Солнца , называется геоцентрическая или гелиоцентрическая гравитационная постоянная .
M{\ displaystyle M}μ{\ displaystyle \ mu}

Фактически, для Земли и Солнца этот продукт известен с большей точностью, чем тот, который связан с каждым из двух факторов и . Таким образом, можно использовать известное значение продукта с большей точностью, вместо того, чтобы заменять значения двух параметров.
грамм{\ displaystyle G}M{\ displaystyle M}

Для Земли : то есть, чтобы сказать до 0,002 частей на миллион частей на миллиард = 2 вблизи, что в 10 000 раз лучше , чем G в одиночку.μзнак равнограммMзнак равно398600 4418±0,0008 kм3⋅s-2{\ displaystyle \ mu = GM = 398 \, 600 {,} 441 \, 8 \ pm 0 {,} 000 \, 8 \ {\ rm {km ^ {3} \ cdot s ^ {- 2}}}}

Для Солнца :, или с точностью до 0,06 частей на миллиард, что в 366 666 раз лучше, чем только G.1,32712440018±0,00000000008×1020 м3⋅s-2{\ displaystyle 1 {,} 327 \, 124 \, 400 \, 18 \ pm 0 {,} 000 \, 000 \, 000 \, 08 \ times 10 ^ {20} \ {\ rm {m ^ {3} \ cdot s ^ {- 2}}}}

Гравитационная постоянная Гаусса

Точно так же расчеты небесной механики могут выполняться в единицах солнечной массы, а не в единицах Международной системы единиц , таких как килограмм .

В этом случае используется гравитационная постоянная Гаусса , которая отмечается :
k{\ displaystyle k}

kзнак равно0,01720209895 В32 D-1 S-12{\ displaystyle k = 0 {,} 017 \, 202 \, 098 \, 95 \ A ^ {\ frac {3} {2}} \ D ^ {- 1} \ S ^ {- {\ frac {1} {2}}}}

с участием:

В{\ displaystyle A}является астрономической единицы ;
D{\ displaystyle D}это средний солнечный день ;
S{\ displaystyle S}- масса Солнца .

Если вместо среднего солнечного дня использовать звездный год как единицу времени , то значение будет очень близко к .
k {\ displaystyle {k} \}2π{\ displaystyle 2 \ pi}

Эксперимент Генри Кавендиша

В конце 18 века британский физик и химик Генри Кавендиш хотел измерить среднюю плотность нашей планеты. В эксперименте ученый использовал крутильные весы и коромысло, которое он закрепил на длинной металлической нити. В него физик положил два свинцовых шара примерно по 730 граммов каждый. К каждому из этих шаров – на одной высоте – Кавендиш подвел тяжелый шар, около 150 кг, также сделанный из свинца. Кавендиш приложил максимум усилий в ходе эксперимента и поместил установку в деревянный ящик, чтобы потоки воздуха и перепады температуры не оказывали на нее никакого влияния.

Результат, как вероятно знает уважаемый читатель, позволил с удовлетворительной точностью измерить плотность Земли и стал первым в истории экспериментом по изучению гравитационного взаимодействия между телами в лабораторных условиях. Отметим также, что полученные Кавендишом данные впоследствии позволили ученым вычислить гравитационную постоянную.

Средняя плотность Земли равна 5,51. Эти значения разделяют два века и подтверждают огромный экспериментальный талант британца Генри Кавендиша.

Важно понимать, что ученый в своем эксперименте не ставил задачу определения гравитационной постоянной, так как в те годы еще не было выработано единого представления о ней в научном сообществе

Из истории гравитационной постоянной

Интересно, что в работах Ньютона нет такой величины. Она появилась в физике существенно позже. Если быть конкретнее, то только в начале девятнадцатого века. Но это не значит, что ее не было. Просто ученые ее не определили и не узнали ее точное значение. Кстати, о значении. Гравитационная постоянная постоянно уточняется, поскольку является десятичной дробью с большим количеством цифр после запятой, перед которой стоит ноль.

Именно тем, что эта величина принимает такое маленькое значение, объясняется то, что действие сил гравитации незаметно на небольших телах. Просто из-за этого множителя сила притяжения оказывается ничтожно маленькой.

Впервые опытным путем установил значение, которое принимает гравитационная постоянная, физик Г. Кавендиш. И случилось это в 1788 году.

В его опытах использовался тонкий стержень. Он был подвешен на тоненькой проволоке из меди и имел длину около 2 метров. К концам этого стержня были прикреплены два одинаковых свинцовых шара диаметром 5 см. Рядом с ними были установлены большие свинцовые шары. Их диаметр был уже 20 см.

При сближении больших и маленьких шаров наблюдался поворот стержня. Это говорило об их притяжении. По известным массам и расстоянию, а также измеренной силе закручивания удалось достаточно точно узнать, чему равно гравитационное постоянное.

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении — явлении притяжения тел к Земле, от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

А началось все со свободного падения тел

Если поместить в пустоту тела разной массы, то они упадут одновременно. При условии их падения с одинаковой высоты и его начала в один и тот же момент времени. Удалось рассчитать ускорение, с которым все тела падают на Землю. Оно оказалось приблизительно равно 9,8 м/с2.

Ученые установили, что сила, с которой все притягивается к Земле, присутствует всегда. Причем это не зависит от высоты, на которую перемещается тело. Один метр, километр или сотни километров. Как бы далеко ни находилось тело, оно будет притягиваться к Земле. Другой вопрос в том, как ее значение будет зависеть от расстояния?

Именно на этот вопрос нашел ответ английский физик И. Ньютон.

История измерения

Гравитационная постоянная фигурирует в современной записи закона всемирного тяготения (b) , однако отсутствовала в явном виде у Ньютона (b) и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная в нынешнем виде впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном (b) в «Трактате по механике» (1809), по крайней мере, никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявленоисточник не указан 1802 дня.

В 1798 году (b) Генри Кавендиш (b) поставил эксперимент (b) с целью определения средней плотности Земли с помощью крутильных весов (b) , которые предложил использовать для этого Джон Мичелл (b) (Philosophical Transactions 1798). Кавендиш сравнивал маятниковые колебания пробного тела (b) под действием тяготения шаров известной массы и под действием тяготения Земли. Численное значение гравитационной постоянной было вычислено позже на основе значения средней плотности Земли. Точность измеренного значения G со времён Кавендиша увеличилась, но и его результат был уже достаточно близок к современному.

Значение этой постоянной известно гораздо менее точно, чем у всех других фундаментальных физических постоянных, и результаты экспериментов по её уточнению продолжают различаться.

В то же время известно, что проблемы не связаны с изменением самой постоянной от места к месту и во времени (неизменность гравитационной постоянной проверена с точностью до ΔG/G ~ 10−17), но вызваны экспериментальными трудностями измерения малых сил с учётом большого числа внешних факторов. В будущем, если опытным путём будет установлено более точное значение гравитационной постоянной, то оно может быть пересмотрено.

В 2013 году значение гравитационной постоянной было получено группой ученых, работавших под эгидой Международного бюро мер и весов (b) :

G = 6,67554(16)⋅10−11 м3·с−2·кг−1 (стандартная относительная погрешность (b) 25 ppm (или 0,0025 %), первоначальное опубликованное значение несколько отличалось от окончательного из-за ошибки в расчётах и было позже исправлено авторами).

В июне 2014 года в журнале «Nature (b) » появилась статья итальянских и нидерландских физиков, где были представлены новые результаты измерения G, сделанные при помощи атомных интерферометров (b) . По их результатам

G = 6,67191(99)⋅10−11 м3·с−2·кг−1 с погрешностью 0,015 % (150 ppm).

Авторы указывают, что поскольку эксперимент с применением атомных интерферометров основан на принципиально других подходах, он помогает выявить некоторые систематические ошибки, не учитывающиеся в других экспериментах.

В августе 2018 года в журнале «Nature (b) » физиками из Китая и России были опубликованы результаты новых измерений гравитационной постоянной с улучшенной точностью (погрешность 12 ppm, или 0,0012 %). Были использованы два независимых метода — измерение времени качаний торсионного подвеса и измерение углового ускорения (b) , получены значения G, соответственно:

G = 6,674184(78)⋅10−11 м3·с−2·кг−1;

G = 6,674484(78)⋅10−11 м3·с−2·кг−1.

Оба результата в пределах двух стандартных отклонений совпадают с рекомендованным значением CODATA, хотя отличаются друг от друга на ~2,5 стандартных отклонения.

Как связана гравитационная постоянная с ускорением свободного падения?

Если сравнить две формулы, одна из которых будет для силы тяжести, а другая для закона тяготения Земли, то можно увидеть простую закономерность. Гравитационная постоянная, масса Земли и квадрат расстояния от центра планеты составляют коэффициент, который равен ускорению свободного падения. Если записать это формулой, то получится следующее:

g = (G х M) : r2.

Причем в ней используются такие обозначения:

Масса Земли	M
Радиус Земли	r

Кстати, гравитационную постоянную можно найти и из этой формулы:

G = (g х r2) : M.

Если требуется узнать ускорение свободного падения на некоторой высоте над поверхностью планеты, то пригодится такая формула:

g = (G х M) : (r + н)2, где н — высота над поверхностью Земли.

История измерения

Гравитационная постоянная фигурирует в современной записи закона всемирного тяготения , однако отсутствовала в явном виде у Ньютона и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная в нынешнем виде впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном в «Трактате по механике» (1809), по крайней мере никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявлено [] .

G
относительная погрешность