Определить среднюю величину по способу моментов

Решения задач методом моментов

Для оценивания неизвестных параметров статистических распределений наравне с методом наибольшего правдоподобия используют метод моментов.

Суть метода: выразить числовые параметры теоретического распределения через моменты распределения, оценненные по выборки. Число моментов должно соответствовать числу неизвестных параметров распределения (чаще всего используют первые два момента). После вычисления приравниваем теоретические и выборочные моменты друг к другу и выражаем оценки параметров.

Данный метод прост в в реализации, дает неплохие оценки и удобен для отработки навыков. Про свойства оценок: состоятельность оценок выполняется при непрерывной зависимости от параметра, асимптотическая эффективность оценок, полученных по ММП всегда лучше чем у ММ, оценки по ММ чаще всего смещенные (требуется проверка).

Примеры нахождения оценок по методу моментов для разных распределений вы найдете ниже. Удачи!

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

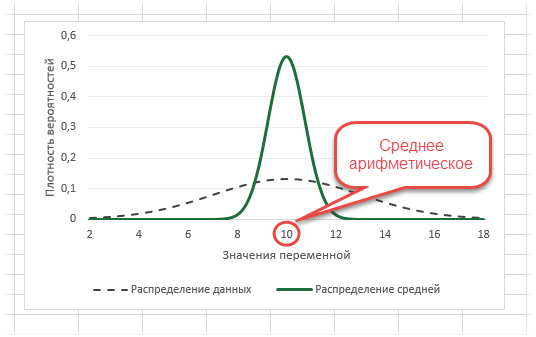
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

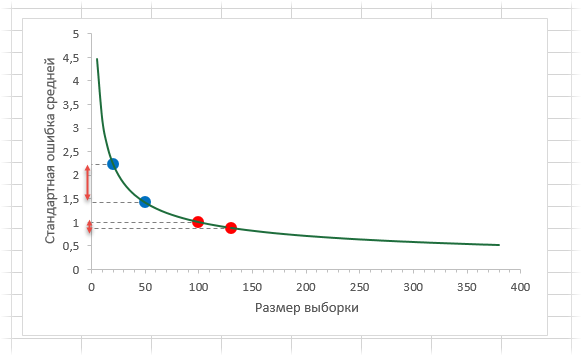
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Задача на определение средней арифметической

Рассчитать средний возраст студентов в группе из 20 человек:

Если сгруппировать данные, то получим ряд распределения:

2. Задача на нахождение средней арифметической взвешенной

Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим, шт., Х _i

Число рабочих, fi

3. Задача на в ычисление средней по групповым средним или по частным средним.

Распределение рабочих по среднему стажу работы

Средний стаж работы, лет.

Число рабочих, чел.,

4. Задача на в ычисление средних в рядах распределения (интервальный ряд).

Распределение рабочих АО по уровню ежемесячной оплаты труда

Группы рабочих по оплате труда у.е.

Число рабочих, чел.

Середина интервала, х i

Задача 5 . Вычисление средних в интервальных рядах методом моментов

Распределение малых предприятий региона по стоимости основных производственных фондов

Группы предприятий по стоимости ОПФ, у.е.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.

Один из вариантов, обладающий наибольшей частотой принимают за А, i — величина интервала.

А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I , получим новый вариационный ряд распределения новых вариантов х _i_. Средняя арифметическая их новых вариантов- момент первого порядка m _i_{= = 0/25=0}

_I*

Задача 6 на определение Средней гармонической.

Заработная плата предприятий АО

Численность промышленно- производственного персонала, чел

Месячный фонд заработной платы, тыс руб.

Средняя заработная плата, руб.

Определить среднюю з/п по всем предприятиям.

Составим логическую формулу средней: средняя з/п по всем предприятиям =

1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.

Искомая средняя величина определяется по средней агрегатной:

_{= =}

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.

_{= =(1046*540+1210*275+1130*458)/1273=1112 руб.}

3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:

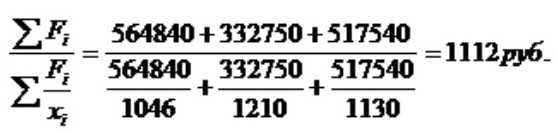
Все ответы верны.

Задача 7. Определить среднюю цену моркови по всем магазинам.

Цена и выручка от реализации по трем коммерческим магазинам.

Цена моркови., руб за кг.

Выручка от реализации, руб.

Решение.

Логическая формула средней: средняя цена моркови =

нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.

Искомая средняя определяется по средней гармонической взвешенной:

Задача 8 по статистике с решением: средние величины.

Информация о вкладах в банке

Число вкладов, тыс., f

Средний размер вклада, руб., x

Сумма вкладов, млн. руб., F

Средний размер вклада, x

Определить средний размер вклада по двум видам.

1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:

₌₌

2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:

Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.

1) Решение задачи по средней арифметической простой:

2) решение по средней арифметической взвешенной

₌₌

Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.

Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная

Источник

Алгоритм нахождения среднего арифметического

Рассмотрим следующую задачу.

Два брата-садовода продавали собранные фрукты. Первый брат продал яблок на 25000 рублей, а второй брат продал груш на сумму 15000 рублей. Все заработанные деньги братья разделили поровну. Сколько денег заработал каждый садовод?

Чтобы ответить на вопрос, необходимо использовать изученное правило.

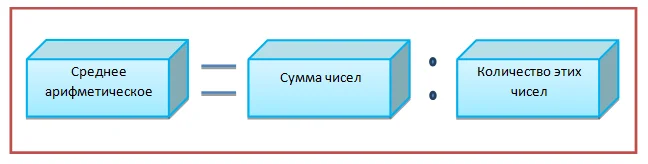
Чтобы найти среднее арифметическое нескольких чисел, нужно сумму этих чисел разделить на их количество. Для этого:1. Определяем количество слагаемых;2. Находим сумму всех слагаемых;3. Делим полученную сумму на количество слагаемых

В начале давайте определим количество слагаемых. Так как фрукты продавали два садовода, то и делить выручку будем между ними. То есть количество слагаемых в сумме – два.

Теперь можем найти общую сумму, заработанную братьями. Для этого, складываем выручку первого и второго брата:

25000+15000=40000

Всего они заработали 40000 рублей.

Зная, что общая сумма равна 40000 рублей, мы можем найти сумму заработка каждого садовода. Для этого полученную сумму (40000) делим на количество слагаемых (2):

40000 : 2 = 20000.

Получается, заработок садовода составил 20000 рублей.

В ходе решения данной задачи мы составили алгоритм нахождения среднего арифметического.

Запомни!

Алгоритм вычисления среднего арифметического:1. Находим слагаемые и считаем их количество;2. Суммируем все слагаемые;3. Полученную сумму делим на количество слагаемых

Держи табличку всегда под рукой, тогда сможешь найти среднее арифметическое любых чисел!

Выполним задание.

Найди среднее арифметическое чисел 10,20,30,40.

Чтобы выполнить необходимые вычисления, вспоминаем,

среднее арифметическое — частное суммы всех слагаемых и их количества

Мы уже знаем, что для вычисления заданий, такого вида, существует специальный алгоритм. Используя данный алгоритм,выполним все необходимые действия.

Следуя определенному алгоритму, мы без труда выполнили задание.

Запомни формулу среднего арифметического!

В заключение нашего урока рассмотрим еще одну задачу.

В школе четыре пятых класса 5А,5Б,5В,5Г. 5А – 22 ученика, 5Б –30 учеников, 5В – 28 детей, 5Г – 20. Найдите, сколько детей училось бы в каждом классе, если во всех классах учеников будет поровну.

Исходя из условия, в этой задаче нужно найти среднее количество учеников в одном классе. Чтобы ответить на главный вопрос, необходимо воспользоваться алгоритмом вычисления среднего арифметического.

Значит, если бы во всех пятых классах школы, училось равное количество учеников, в каждом классе было по 25 детей.

Запишем решение.

Сегодня вы узнали, как найти среднее арифметическое число. Внимательно рассмотрите урок, и запомните основные определения и алгоритмы! Тогда, любая контрольная будет по плечу!

Понятие среднего арифметического

К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?

Ответ на вопрос, можно получить двумя способами. Рассмотрим их.

Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.

Разделим конфеты между детьми:

18 : 3 = 6.

Теперь известно, что каждому ребенку досталось 6 конфет.

Разделим шоколадки:

6 :3 = 2.

Каждой внучке досталось две шоколадки.

Разделим шоколадные яйца:

6 : 3 = 2.

Выяснили, бабушка привезла по два киндер-сюрприза.

Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:

6+2+2=10.

Получается, бабушка привезла по 10 сладостей.

Запишем решение задачи.

Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.

Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть. Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:

Среднее арифметическое нескольких чисел — результат деления суммы этих чисел на их количество

Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:

18+6+6=30.

Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:

30 : 3 =10.

Каждой внучке досталось по 10 сладостей.

Запишем решение этой задачи с использованием второго способа.

Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!

1 Расчет дисперсии способом моментов

Вычисление дисперсий связано с громоздкими расчетами (особенно если средняя величина выражена большим числом с несколькими десятичными знаками). Расчеты можно упростить, если использовать упрощенную формулу и свойства дисперсии.
Дисперсия обладает следующими свойствами:

если все значения признака уменьшить или увеличить на одну и ту же величину А, то дисперсия от этого не уменьшится:

, то или
Используя свойства дисперсии и сначала уменьшив все варианты совокупности на величину А, а затем разделив на величину интервала h, получим формулу вычисления дисперсии в вариационных рядах с равными интервалами способом моментов:
,

где – дисперсия, исчисленная по способу моментов;
h – величина интервала вариационного ряда; – новые (преобразованные) значения вариант;
А– постоянная величина, в качестве которой используют середину интервала, обладающего наибольшей частотой; либо вариант, имеющий наибольшую частоту; – квадрат момента первого порядка; – момент второго порядка.
Выполним расчет дисперсии способом моментов на основе данных о сменной выработке рабочих бригады.
Таблица 4 – Расчет дисперсии по способу моментов

Группы рабочих по выработке, шт.	Число рабочих,	Середина интервала,	Расчетные значения

Порядок расчета:

рассчитываем дисперсию:

Интересные факты

По статистике, дети улыбаются 400 раз в день, а взрослые всего 17. Улыбайтесь чаще!

В России продолжительность жизни мужчин составляет 70 лет, женщин – 78 лет!

Ежедневно в Росси рождается 5000 детей.

Ученые подсчитали, за всю жизнь, человек тратит 5 лет на процесс приема пищи,

Ученые подсчитали, за 70 лет, человек поглощает более 50000 килограммов пищи, в том числе около 200-300 килограммов поваренной соли. Так же, каждый человек, достигший 70 летнего возраста, выпил за всю жизнь 50000 литров воды, что больше в 1400 раз массы человеческого тела.

Одной хорошей шариковой ручкой можно написать 50000 слов.

Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.

Примеры решений

Пример 1. Число семян сорняков в пробах зерна подчинено закону Пуассона. Имеется выборка проб зерна. Результаты записаны в таблице Т1. Найти параметр $\lambda$ по выборке методом моментов.

Пример 2. При условии равномерного распределения случайной величины $Х$ произведена выборка 3 5 7 9 11 13 15 17 19 21 21 16 15 26 22 14 21 22 18 25 Найти оценку параметров $a$ и $b$ по методу моментов.

Пример 3. Найти методом моментов по выборке $x_1, x_2, . x_n$ точечную оценку параметра $p$ биномиального распределения $P_m(x_i)=C_^ p^ (1-p)^$, где $x_i$ — число появлений события в $i$-ом опыте ($i=1,2. n$), $m$ — количество испытаний в одном опыте.

Пример 4. Найти методом моментов по выборке $x_1, x_2, . x_n$ точечные оценки неизвестных параметров $a$ и $\sigma$ нормального распределения.

Пример 5. Пусть случайная величина $\xi$ имеет плотность $p(x)=1/(b-a)$, если $x\in(a;b)$, и $p(x)=0$, иначе. Произведена выборка. Используя метод моментов, найти $a$ и $b$.

Основные понятия и определения по теме

Средние величины используются в здравоохранении:

для оценки здоровья населения (показатели физического развития, средняя длительность пребывания на больничном листе и т.д.);
для оценки деятельности лечебно-профилактических учреждений (средняя длительность работы койки в году, оборот койки и т.д.);
для планирования (число жителей на терапевтическом, педиатрическом участке, стоимость одного койко-дня и т.д.);
для оценки санитарно-гигиенических параметров (освещенность, температура, влажность воздуха и т.д.);
для определения разовых доз лекарственных веществ и т.д.

средних величинСредние величины обладают тремя свойствами:

средняя занимает срединное положение в вариационном ряду;
средняя выражает общую меру изучаемого явления;
сумма отклонений всех вариант от средней равна нулю.

Наиболее широко используются три средние величины:

мода (Мо) – соответствует величине признака, который чаще встречается в статистической совокупности, т.е. варианте наиболее часто встречающейся в вариационном ряду;
медиана (Ме) – варианта, занимающая срединное положение в вариационном ряду и делящая его пополам. Для того, чтобы узнать значение медианы, необходимо определить порядковый номер варианты, занимающей срединное положение (n/2), где n – число вариант в вариационном ряду. При нечетном числе вариант используется формула n+1/2;
средняя арифметическая (простая, взвешенная).

Вариационный рядВариационный ряд может быть:

простой, несгруппированный;
сгруппированный;
прерывный или непрерывный;
правильный или неправильный;
ранжированный или неранжированный.

Обозначения, используемые в вариационном ряду:

варианта (V) – отдельное числовое выражение изучаемого признака;
частота (р) – количество вариант определенной величины;
число наблюдений (n) – общее число вариант в вариационном ряду.

Пример:

V	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	p=45
p	1	2	2	2	3	3	4	5	6	4	3	2	2	2	1	1	1	1
d	-8	-7	-6	-5	-4	-3	-2	-1	1	2	3	4	5	6	7	8	9	dp=-23
dp	-8	-14	-12	-10	-12	-9	-8	-5	4	6	6	8	10	6	7	8	9

Мода (Мо)Медиана (Ме)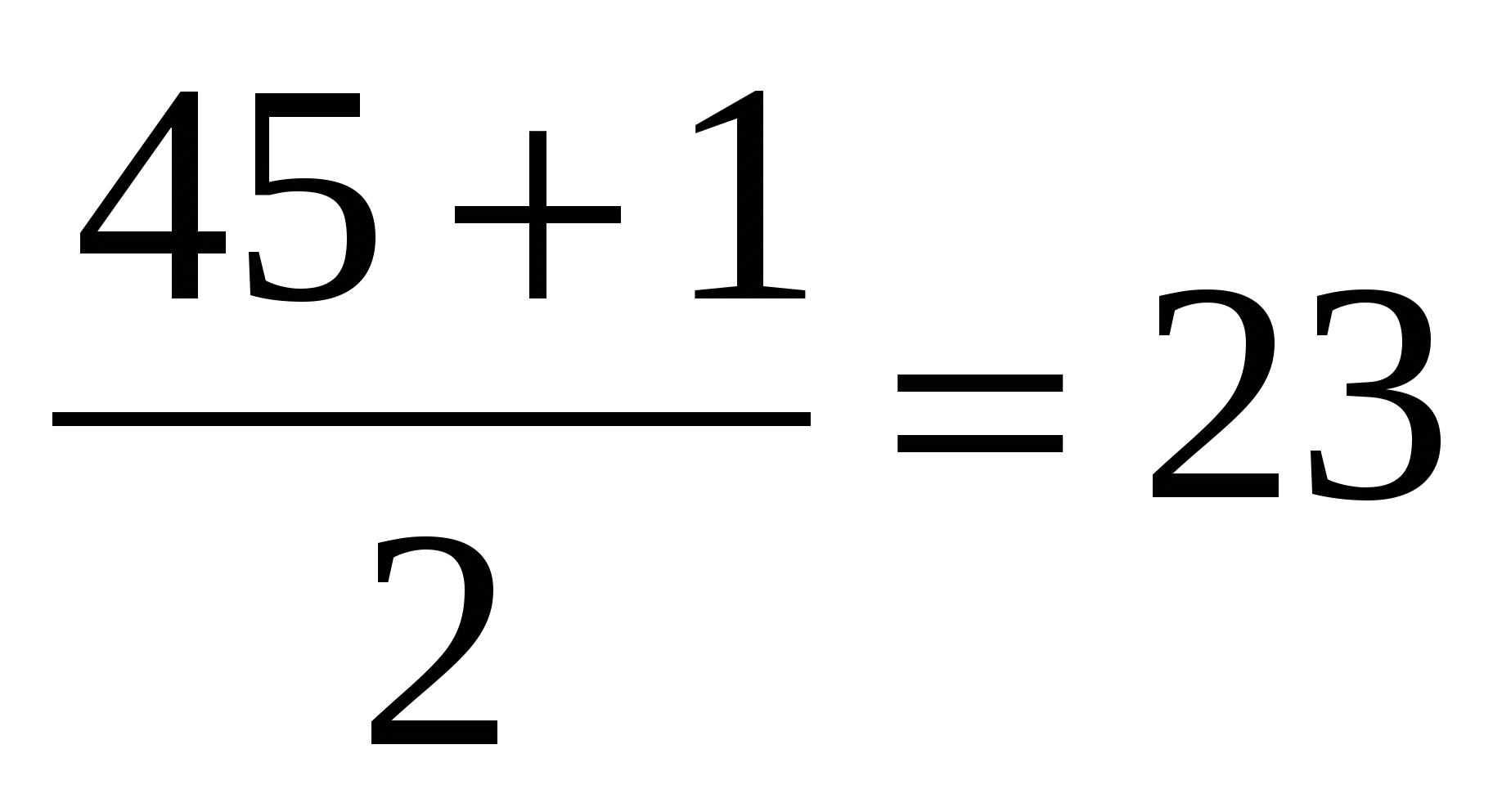Средняя арифметическаяДля вычислениядва способа:среднеарифметический способ и способ моментов.среднюю арифметическую простуюиспользуя среднеарифметический способ: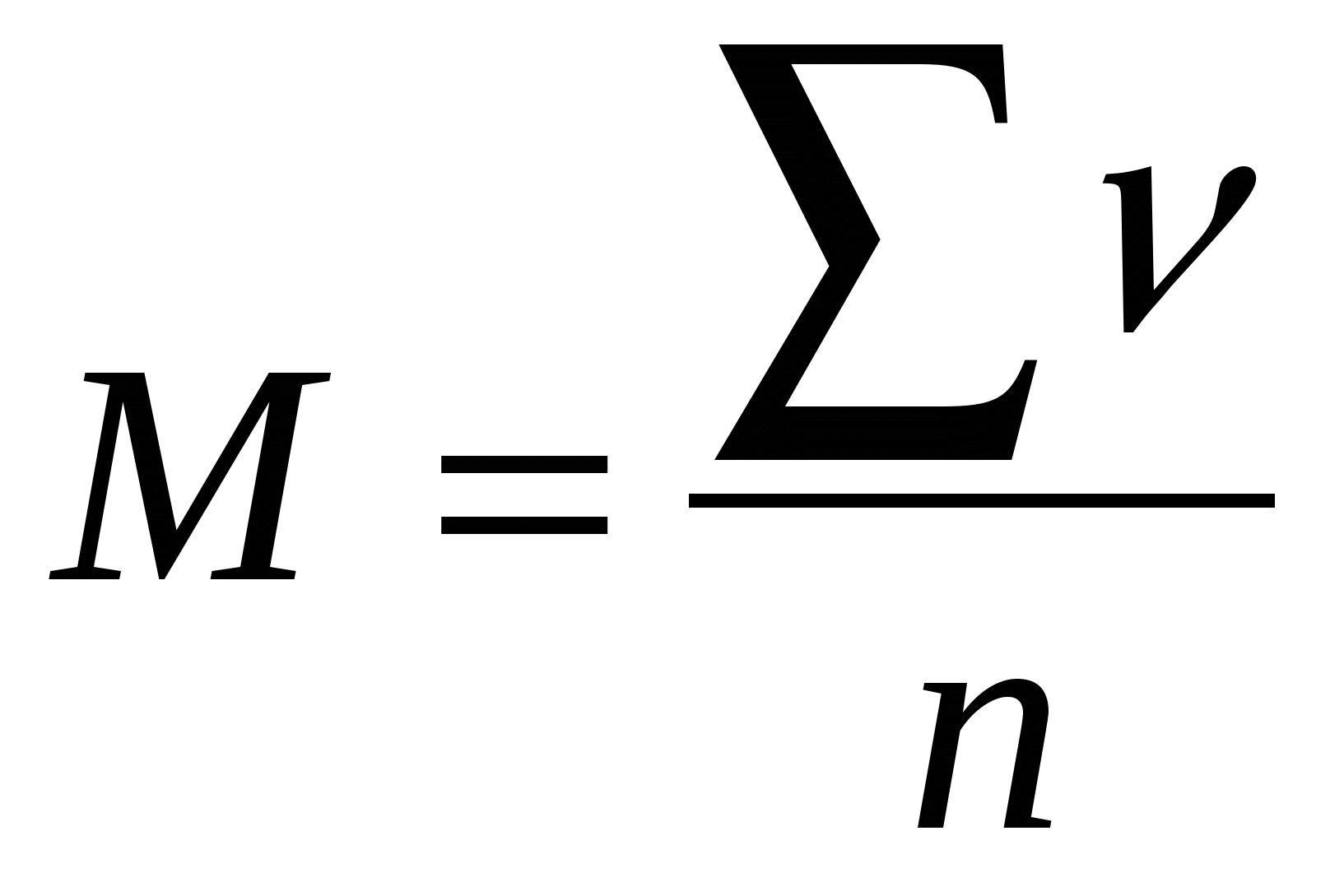среднюю арифметическую взвешеннуюсреднеарифметическому способуПо способу моментовсгруппированного ряда

определение V_min и V_max V_min=3, V_max=20;
определение количества групп (по таблице);
расчет интервала между группами ;
определение начала и конца групп;
определение частоты вариант каждой группы (таблица 2).

Методика построения сгруппированного ряда

Длительность лечения в днях (V)	Число больных (р)	V ср. гр.	Vxp	d=V-Mo	d*p	d2	d2*p
3-5	5	4	20	-6	-30	36	180
6-8	8	7	56	-3	-24	9	72
9-11	15	10	150
12-14	9	13	117	3	27	9	81
15-17	5	16	80	6	30	36	180
18-20	3	19	57	9	27	81	243
n=45 Vp=480 dp=30 d2p=766

Преимущество сгруппированного вариационного рядагрупповых свойств генеральной совокупностиразнообразие признакакритериями

лимит (lim),
амплитуда (Amp),
среднеквадратическое отклонение (),
коэффициент вариации (С).

Лимит (lim)_min_maxАмплитуда (Amp)_max_minдва способа расчетасреднеарифметический и способ моментовварианты от средней вариационного ряда_max_min_max_minТаблица значений k (по С.И. Ермолаеву)

	1	2	3	4	5	6	7	8	9
–	–	1,13	1,69	2,06	2,33	2,53	2,70	2,85	2,97
10	3,08	3,17	3,26	3,34	3,41	3,47	3,53	3,59	3,64	3,69
20	3,73	3,78	3,82	3,86	3,90	3,93	3,96	4,00	4,03	4,06
30	4,09	4,11	4,14	4,16	4,19	4,21	4,24	4,26	4,28	4,30
40	4,32	4,34	4,36	4,38	4,40	4,42	4,43	4,45	4,47	4,48
50	4,50	4,51	4,53	4,54	4,56	4,57	4,59	4,60	4,61	4,63
60	4,64	4,65	4,66	4,68	4,69	4,70	4,71	4,72	4,73	4,74
70	4,75	4,77	4,78	4,79	4,80	4,81	4,82	4,83	4,83	4,84
80	4,85	4,86	4,87	4,88	4,89	4,90	4,91	4,91	4,92	4,93
90	4,94	4,95	4,96	4,99	4,97	4,98	4,99	4,99	5,00	5,01
	100	200	300	400	500	600	700	800	900	1000
К	5,02	5,49	5,76	5,94	6,07	6,18	6,28	6,35	6,42	6,48

Таблица коэффициентов Пирсона

n	2	4	6	8	10	20	30	40	50
К	0,89	0,49	0,39	0,35	0,32	0,27	0,24	0,23	0,22

сравнения разнообразия двух средних величинкоэффициент вариации (C_V)_V_V_Vкоэффициент асимметрии_а_а_а
8

	Программа квалификационного экзамена по специальности медицинская реабилитология 14. 00. 12Программа предназначена для подготовки и сдачи квалификационного экзамена по специальности медицинская реабилитология и содержит…		Министерство здравоохранения Республики Узбекистан Ташкентская медицинская академия Кафедра факультетской и госпитальной хирургии лечебного факультетаЗаведующим кафедрой является академик Каримов Ш. И. На кафедре работают профессора Асраров А. А., Кротов Н. Ф., Хакимов М. Ш., доценты…
	Ўзбекистон Республикаси Давлат статистика қўмитасининг 2009 йил 16 ноябрдаги 5 сонли қароригаКичик корхона ва микрофирмалар – асосий фаолият тури саноат ишлаб чиқаришга асосланган юридик шахслар (Давлат статистика қўмитаси…		Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат
	Ўзбекистон Республикаси Давлат статистика қўмитасининг 2009 йил 16 ноябрдаги 4–сонли қароригаДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат статистика…		Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат
	Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат		Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат
	Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат		Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат
	Ушбу ҳисобот шакли статистика органлари томонидан бепул тақдим этилади, Ўзбекистон Республикаси Давлат статистика қўмитасининг расмий рухсатисиз тираж қилинмайди ва тижорат мақсадида тарқатилмайдиДавлат статистика кузатувини олиб бориш учун зарур бўлган ҳисобот ва бошқа маълумотларни тақдим этмасликда ифодаланган давлат