Дифракция света. принцип гюйгенса-френеля. зоны френеля

Принцип Гюйгенса-Френеля. Дифракція світла

Дифракцією називається сукупність явищ, що спостерігаються при поширенні світла в середовищі з різними неоднорідностями (поблизу границь непрозорих або прозорих тіл, через малі отвори) і які пов’язані із зміною напрямку поширення світлових хвиль (порівняно з напрямком, передбаченим геометричною оптикою).

Дифракція, зокрема, приводить до огинання світловими хвилями перешкод і проникнення світла в область геометричної тіні.

Між інтерференцією і дифракцією немає суттєвої фізичної відмінності.

 Інтерференція хвиль – це перерозподіл інтенсивності, який виникає в результаті суперпозиції хвиль, що збуджуються скінченним джерелом когерентних джерел.

Перерозподіл інтенсивності, який виникає внаслідок суперпозиції хвиль, що збуджуються когерентними джерелами, які розміщені неперервно, називається дифракцією хвиль.

Явище дифракції пояснюється за допомогою принципу Гюйгенса

кожна точка, до якої доходить хвиля, служить центром вторинних хвиль, а обвідна цих хвиль дає положення хвильового фронту в наступний момент часу.

Як приклад застосування принципу Гюйгенса розглянемо падіння плоскої хвилі на перешкоду з отвором (рис.220).

Коли хвильовий фронт доходить до перешкоди, то кожна точка отвору стає джерелом вторинних хвиль, а обвідна цих хвиль задає фронт хвилі, що пройшла через отвір. Цей фронт плоский лише в се­редній частині, а біля границі отвору відбувається загинання хвильового фронту, тобто хвиля проникає в область геометрич­ної тіні, огинаючи краї перешкоди.

Принцип Гюйгенса – суто геометричний спосіб побудови хвильових поверхонь –  розв’язує лише задачу про напрямок поширення хвильового фронту, але не зачіпає, по суті, питання про амплітуду, а отже, і про інтенсивність хвиль, що поширюються в різних напрямках. Френель вклав у принцип Гюйгенса фізичний зміст, доповнивши його ідеєю інтерференції вторинних хвиль.

•  Принцип Гюйгенса-Френе­ля можна виразити такими положеннями:
• 1).    під час розрахунку амплітуди світло­вих коливань, що збуджуються джерелом   в довільній точці М, джерело   можна замінити еквівалентною йому системою вторинних джерел – малих ділянок dS будь-якої замкненої допоміжної поверхні S, проведеної так, щоб вона охоплювала джерело   і не охоплювала розглядувану точку М;
• 2).    вторинні джерела, які еквівалентні джерелу  , когерентні між собою, тому вторинні хвилі, збуджені ними, інтерферують, і розрахунок інтерференції найбільш простий, якщо S – хвильова поверхня для світла джерела  , оскільки при цьому фази коливань всіх вторинних джерел однакові;

3).    амплітуда   коливань, що збуджуються в точці М вторинним джерелом, пропорційна до площі dSвідповідної ділянки хвильової поверхні обернено пропорційна до від­стані r від неї до точки М і залежить від кута   між зов­нішньою нормаллю до хвильової поверхні і напрямком від елемента dS до точки М (рис. 221):

,

де   – фаза коливань в місці розміщення хвильової поверхні, a – величина, яка пропорційна до амплітуди первинних хвиль в точках елемента dS;   монотонно спадає від 1 при   до при   (вторинні джерела не випромінюють назад); кут   називається кутом дифракції.

4).    якщо частина поверхні S закрита не­прозорими екранами, то вона не випро­мінює енергію, а інші випромінюють так само, як і за відсутності екранів.

Врахування амплітуд і фаз вторинних хвиль дозволяє в кожному конкретному випадку знайти амплітуду результуючої хвилі в довільній точці простору, тобто визначити закономірності поширення світла.

В загальному випадку розрахунок інтерференцій вторинних хвиль досить складний і громіздкий, однак для ряду випадків знаходження амплітуди результуючого коливання здійснюється алгебраїчним або геометричним додаванням.

1. Результуюче коливання в точці М є суперпозицією коливань , взятих для всієї хвильової поверхні S:
2. .
3. Ця формула є аналітичним виразом принципу Гюйгенса-Френеля.

Расчет интерференционной картины от двух источников.

Расчет интерференционной картины от
двух когерентных источников.

Рассмотрим две когерентные световые
волны, исходящие из источников
и(рис.1.11.).

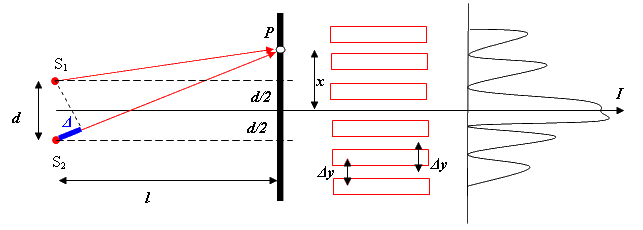
Экран для наблюдения интерференционной
картины (чередование светлых и темных
полос) поместим параллельно обеим щелям
на одинаковом расстоянии
.Обозначим
за x — расстояние от центра интерференционной
картины до исследуемой точки Р на
экране.

Расстояние между источниками
иобозначим
какd
. Источникиирасположены
симметрично относительно центра
интерференционной картины. Из рисунка
видно, что

Следовательно

и оптическая разность хода равна

Разность хода
составляет
несколько длин волн и всегда значительно
меньшеи,
поэтому можем считать, чтои.
Тогда выражение для оптической разности
хода будет иметь следующий вид:

Так как расстояние от источников до
экрана во много раз превосходит
расстояние от центра интерференционной
картины до точки наблюдения
,
то можно допустить, чтот.
е.

Подставив значение
(1.95)
в условие (1.92) и выразив х, получим, что
максимумы интенсивности будут наблюдаться
при значениях

, (1.96)

где
—
длина волны в среде, аm
— порядок
интерференции, ах
max
—
координаты максимумов интенсивности.

Подставив (1.95) в условие (1.93), получим
координаты минимумов интенсивности

, (1.97)

На экране будет видна интерференционная
картина, которая имеет вид чередующихся
светлых и темных полос. Цвет светлых
полос определяется светофильтром,
используемым в установке.

Расстояние между соседними минимумами
(или максимумами) называется шириной
интерференционной полосы. Из (1.96) и
(1.97) следует, что эти расстояния имеют
одинаковое значение. Чтобы рассчитать
ширину интерференционной полосы, нужно
из значения координаты одного максимума
вычесть координату соседнего максимума

Для этих целей можно использовать и
значения координат двух любых соседних
минимумов.

Дисперсия света

Дисперсия света – это зависимость показателя преломления среды от длины волны (частоты) падающего на вещество света.

Опыт Ньютона (1672)

Из-за дисперсии световые волны с различной длиной волны поразному преломляются веществом, что приводит к разложению белого света на цветные монохроматические лучи – спектр.

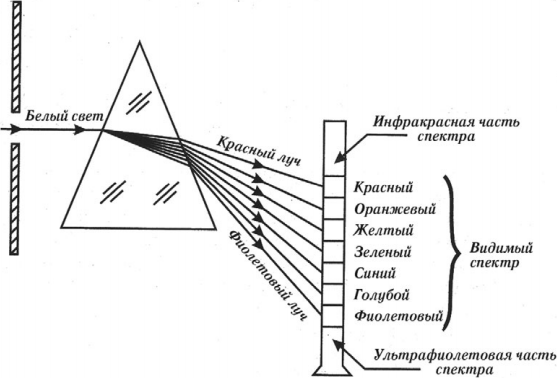
Для лучей света различной цветности показатели преломления данного вещества различны, т. к. различны скорости распространения электромагнитных волн, у которых разная длина волны. Луч красного света преломляется меньше из-за того, что красный свет имеет в веществе наибольшую скорость, а луч фиолетового цвета преломляется больше, так как скорость для фиолетового цвета наименьшая. Это объясняется особенностями взаимодействия этих волн с электронами, входящими в состав атомов и молекул вещества среды, где они движутся.

Дисперсией света объясняется такое природное явление, как радуга.

Принцип Гюйгенса — Всё для чайников

Подробности Категория: Оптика

Законы отражения и преломления света можно вывести из одного общего принципа, описывающего поведение волн. Этот принцип впервые был выдвинут современником Ньютона Христианом Гюйгенсом.

Принцип Гюйгенса. Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

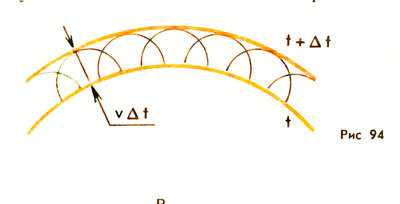
Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t +Δt, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис. 94).

Этот принцип в равной мере пригоден для описания распространения волн любой природы: механических, световых и т. д. Гюйгенс сформулировал его первоначально именно для световых волн.

Закон отражения. С помощью принципа Гюйгенса можно вывести закон, которому подчиняются волны при отражении от границы раздела сред.

Рассмотрим отражение плоской волны. Волна называется , плоской если поверхности равной фазы (волновые поверхности) представляют собой плоскости. На рисунке 95     MN — отражающая поверхность, прямые А1А и В1В— два луча падающей плоской волны (они параллельны друг другу). Плоскость АС—волновая поверхность этой волны.

Угол а между падающим лучом и перпендикуляром к отражающей поверхности в точке падения называют углом падения.Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности АС достигают отражающей границы неодновременно.

Возбуждение колебаний в точке А начнется раньше, чем в точке В, на время Δt=CB/v (v — скорость волны).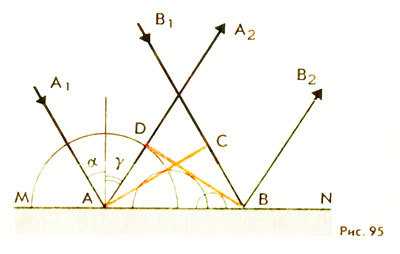

В момент, когда волна достигнет точки Вив этой точке начнется возбуждение колебаний, вторичная волна с центром в точке А уже будет представлять собой полусферу радиусом r = AD = vΔt = CB. Радиусы вторичных волн от источников, расположенных между точками А и В, меняются так, как показано на рисунке 95. Огибающей вторичных волн является плоскость , касательная к сферическим поверхностям. Она представляет собой волновую поверхность отраженной волны. Отраженные лучи АА2 и ВВ2 перпендикулярны волновой поверхности    DB. Уголϒ между перпендикуляром к отражающей поверхности и отраженным лучом называют углом отражения.

Так как AD=СВ и треугольники ADB и АСВ прямоугольные, то ∠ DBA = ∠CAB и ϒ=∠DBA как углы с перпендикулярными сторонами. Следовательно, угол отражения равен углу падения:

а=ϒ

Кроме того, как вытекает из построения Гюйгенса, падающий луч, луч отраженный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости.

Эти два утверждения представляют собой закон отражения света.Если обратить направление распространения световых лучей, то отраженный луч станет падающим, а падающий — отраженным.

Обратимость хода световых лучей — их важное свойство. Сформулирован общий принцип распространения волн любой природы — принцип Гюйгенса

Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент. Из принципа Гюйгенса выведен закон отражения волн

Сформулирован общий принцип распространения волн любой природы — принцип Гюйгенса. Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент. Из принципа Гюйгенса выведен закон отражения волн.

Измерение скорости света               

Механические модели волн. 1.                

Механические модели волн. 2.                 

Диаграмма направленности диполя                  

Спектр модулированного колебания                  

Принцип суперпозиции. Модель на осциллографе                   

Частота сигнала и характерное время прибора                    

«Стоячая волна» на экране осциллографа                    

Построение изображений в линзах

Для построения изображения в линзах следует помнить:

1. луч, идущий вдоль главной оптической оси линзы, не преломляется;
2. луч, проходящий через оптический центр линзы, не преломляется;
3. луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
4. луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
5. луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
6. произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
7. произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.

Изображение, даваемое тонкой линзой, может быть действительным или мнимым.

Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.

Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.

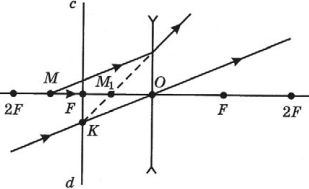
Построение изображений точки, даваемых собирающей линзой

Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.

Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.

Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.

Если точка находится в фокусе линзы, то его изображение находится в бесконечности.

Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.

Построение изображений предмета, даваемых собирающей линзой

Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.

Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.

Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.

Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.

Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.

Построение изображений точки, даваемых рассеивающей линзой

В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.

Построение изображений предмета, даваемых рассеивающей линзой

Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.

Важно!
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние

Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.

При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.

Дифракция механических волн

Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.

На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.

Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней. Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения

Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает

Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.

Дифракция — явление отклонения от прямолинейного распространения волн.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.

Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.

Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.

Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.

Линзы. Оптическая сила линзы

Линза – это прозрачное тело, ограниченное двумя сферическими или криволинейными поверхностями, одна из которых может быть плоской.

Тонкая линза – физическая модель линзы, в которой ее толщиной можно пренебречь по сравнению с диаметром линзы.

Классификация линз

1. По форме:

• выпуклые – это линзы, у которых средняя часть толще, чем края;
• вогнутые – это линзы, у которых края толще, чем средняя часть.

2. По оптическим свойствам:

собирающие – это линзы, после прохождения которых параллельный пучок лучей собирается в одной точке;

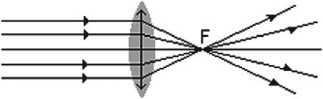
рассеивающие – это линзы, после прохождения которых параллельный пучок лучей рассеивается.

Условные обозначения:

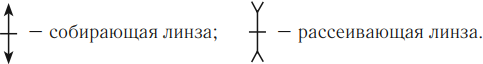
Величины, характеризующие линзу

Главная оптическая ось – это прямая, проходящая через центры сферических поверхностей линзы.

Оптический центр линзы – это точка пересечения главной оптической оси с линзой, проходя через которую луч не изменяет своего направления.

Побочная оптическая ось – это любая прямая, проходящая через оптический центр линзы под произвольным углом к главной оптической оси.

Фокус линзы – это точка, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси.

Обозначение – ​\( F \)​.

Фокусное расстояние – это расстояние от оптического центра линзы до ее фокуса. Обозначение – \( F \), единица измерения – м.

Фокальная плоскость – это плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.

Побочный фокус – это точка пересечения побочной оптической оси с фокальной плоскостью.

Оптическая сила линзы – это величина, обратная фокусному расстоянию.

Обозначение – ​\( D \)​, единица измерения – диоптрия (дптр):

1 дптр – это оптическая сила линзы с фокусным расстоянием 1 м.

Важно!
Оптическая сила линзы зависит от показателя преломления линзы и от радиусов кривизны сферических поверхностей, ограничивающих линзу:

где ​\( n_л \)​ – показатель преломления линзы, ​\( n_{ср} \)​ – показатель преломления среды, ​\( R_1 \)​ и \( R_2 \) – радиусы сферических поверхностей.

Если поверхности выпуклые, то ​\( R_1 \)​ > 0 и \( R_2 \) > 0, если поверхности вогнутые, то \( R_1 \) < 0 и \( R_2 \) < 0.

Если одна из поверхностей линзы плоская, например первая, то ​\( R_1\to\infty \)​, а вторая поверхность выпуклая: \( R_2 \) > 0, то

Классическое объяснение явления [ править | править код ]

Во времена Ньютона из-за недостатка сведений о природе света дать полное объяснение механизма возникновения колец было крайне трудно. Ньютон установил связь между размерами колец и кривизной линзы; он понимал, что наблюдаемый эффект связан со свойством периодичности света, но удовлетворительно объяснить причины образования колец удалось лишь значительно позже Томасу Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстаёт от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

Δ = m λ <displaystyle Delta =mlambda > — max,

где m <displaystyle m> — любое целое число, λ <displaystyle lambda > — длина волны.

Напротив, если вторая волна отстаёт от первой на нечётное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах, и волны гасят друг друга.

Δ = ( 2 m + 1 ) λ 2 <displaystyle Delta =(2m+1)<lambda over 2>> — min,

где m <displaystyle m> — любое целое число, λ <displaystyle lambda > — длина волны.

Для учёта того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода (разность оптических длин пути).

Если n r <displaystyle nr> — оптическая длина пути, где n <displaystyle n> — показатель преломления среды, а r <displaystyle r> — геометрическая длина пути световой волны, то получаем формулу оптической разности хода:

n 2 r 2 − n 1 r 1 = Δ . <displaystyle n_<2>r_<2>-n_<1>r_<1>=Delta .>

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами тёмных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на π <displaystyle pi > ; этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы.

Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

r k = ( k − 1 2 ) λ R n , <displaystyle r_=<sqrt <left(k-<1 over 2>
ight)<frac <lambda R>>>>,>

где R <displaystyle R> — радиус кривизны линзы, k = 1 , 2 , . . . , <displaystyle k=1,2. > λ <displaystyle lambda > — длина волны света в вакууме, n <displaystyle n> — показатель преломления среды между линзой и пластинкой.

Радиус k-го тёмного кольца Ньютона в отражённом свете определяется в соответствии с формулой:

r k = k λ R n , <displaystyle r_=<sqrt >>>,>