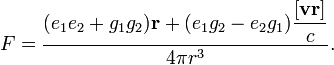Секреты магнитного монополя

Введение

Магни́тный монопо́ль — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд определяет напряжённость магнитного поля совершенно так же, как электрический заряд определяет напряжённость электрического поля.

Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у обычного магнита всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Все известные элементарные частицы, обладающие электромагнитным полем, являются магнитными диполями.

Искусственный спиновый лед

Если пытаться складывать из тетраэдров решетку так, чтобы соединять положительные вершины молекул воды с отрицательными вершинами и сохранять расстояния между ионами кислорода равными 2.76, то будут получаться либо гексагональный, либо кубический лед, причем на каждой водородной связи для протонов будет по две возможные позиции.

Так как число возможных позиций вдвое больше числа протонов, то распределить протоны по ним можно многими способами. Не имея возможности экспериментально определить положение протонов на связях, Бернал и Фаулер предположили, что распределение протонов должно удовлетворять двум ограничениям. Первое из ограничений, сохранение структуры молекулы воды, является достаточно обоснованным, так как энергия водородной связи около 0.4эВ, а энергия отрыва протона от молекулы воды намного больше, около 7.0эВ. Сохранение структуры молекулы воды можно сформулировать так: при распределении протонов по возможным позициям вблизи каждого иона кислорода должно быть два и только два протона. Второе ограничение следует из минимизации кулоновской энергии взаимодействия между протонами и формулируется так: на каждой водородной связи может находиться один и только один протон. Эти два правила получили название правил льда или правил Бернала-Фаулера, а распределения протонов, удовлетворяющие этим правилам, стали называть конфигурациями Бернала – Фаулера.

В 1933 году была опубликована экспериментальная работа Жиока и Эшли , основной результат которой сводился к обнаружению очень большой энтропии льда при низких температурах. В 1935 году Полинг получил для числа конфигураций Бернала-Фаулера простую и достаточно точную оценку G=(3/2)N, где N число молекул воды в кристалле . Более того, зная о работах , он высказал удивительную гипотезу: все конфигурации Бернала-Фаулера имеют одинаковую энергию. Гипотеза Полинга приводила к остаточной, то есть к ненулевой энтропии при нулевой абсолютной температуре, равной S0=Bh(G)/A 0.5598-10 Дж-К»1 (1.1) и качественно объясняла экспериментальный результат . Можно также сказать, что гипотеза Полинга приводила к нарушению третьего закона термодинамики о стремлении энтропии любой физической системы к нулю при стремлении к нулю температуры. Фактически гипотеза Полинга означала, что основное состояние обыкновенного льда экспоненциально вырождено, несмотря на кажущееся очевидным нарушение этого вырождения дальнодействующим кулоновским взаимодействием между протонами. Вскоре Жиок и Стаут провели более точное измерение остаточной энтропии льда и получили для нее значение SF =(0.570±0.03)-10-23Дж-К-1 (1.2) что очень точно совпадало с теоретическим результатом Полинга. Таким образом, экспериментальный результат работы подтверждает гипотезу Полинга. В последующие годы были уточнены как теоретический, так и экспериментальный результаты относительно остаточной энтропии. Так в работе получена более точная теоретическая оценка 0.5661 Ю- ДжК-1, а в работе соответственно был уточнен экспериментальный результат (0.5659±0.0316)10 23ДжК 1. Согласие между экспериментом и теорией стало еще более точным, и это удивительно точное согласие можно считать косвенным подтверждением правил льда и гипотезы Полинга. Прямое подтверждение правил льда было получено значительно позднее методом рассеяния медленных нейтронов .

С теоретической точки зрения гипотеза Полинга кажется на первый взгляд совершенно необоснованной. Действительно, между протонами существуют кулоновское взаимодействие, которое убывает с расстоянием медленно, как \1г и которое, на первый взгляд, для различных распределений протонов должно давать различную энергию. Но экспериментальные результаты говорят в пользу гипотезы Полинга и заставляют провести более детальное теоретическое исследование этого вопроса. В работе для описания протонов во льду был получен псевдо-спиновый гамильтониан следующего вида н= ші3тЬм (13) где J — константа дипольного взаимодействия, равная примерно 0.35эВ, псевдоспиновые переменные сг = ±1 в зависимости от положения протона на связи, ег -единичные вектора вдоль водородных связей, г1} — единичные вектора между серединами связей с индексами ij, rtJ — соответствующее расстояние между центрами связей в единицах длины водородной связи. Из этой формулы следуют сразу два важных вывода. Во-первых, при учете взаимодействия только между ближайшими соседями гамильтониан принимает вид н= ИаЪ (1.4) 2 ( А причем J 0. Здесь суммирование идет только по парам ближайших соседей. Гексагональный и кубический лед содержат правильные тетраэдры или правильные треугольники из ближайших соседей (смотри рисунок 1.3):

обсуждение

Мы можем поместить эти результаты в контекст соответствующей диаграммы состояний (по существу, фазовой диаграммы Т * в сравнении с х ) для ограниченного примитивного модельного электролита, базовой модели поведения электролита. В случае сплошного электролита на этой диаграмме отмечены три значимые границы, соответственно, начало значительной димеризации, минимум проводимости и разделение фаз (см., Например, рис. 1 в ссылке 25). В Dy ₂ Ge ₂ O ₇ мы достигли первой из этих границ для спинового льда. Чтобы достичь других границ, нам потребуется найти материал для раскручивания льда с | ν | ≪ 3.3 K. Однако решетчатый кулоновский газоподобный спиновый лед может демонстрировать еще более сложное фазовое поведение в этом пределе, включая упорядоченные по заряду фазы 26, 27 . Фактически, предельный предел настройки химического потенциала монополя на ν ≪ 3 K уже был определен посредством численных исследований на модели дипольного спинового льда 14 . На монопольном языке эта структура состоит из порядка «двойных зарядов» ± 2 Q, чтобы создать магнитную структуру с «4 спинами в / 4 спинами» на альтернативных тетраэдрах. Эта структура (также известная как структура FeF ₃ ) становится стабильной при ν = 2, 4 К, J _eff = 0, 2 К. В неисследованной области между ν ≈3, 3 К и ν ≈ 2, 4 К мы ожидаем найти много интересного физика связана с увеличением монопольных корреляций и постепенным появлением двойных зарядов. Наши результаты показывают, что эта область должна быть доступна для эксперимента, так как мы показали, как методы высокого давления позволяют резко изменить химический потенциал магнитных монополей в спиновом льду до такой степени, что могут быть обнаружены новые аспекты физики монополей.

Пробоподготовка и характеристика

Партии до 50 мг германата пирохлора диспрозия, Dy ₂ Ge ₂ O ₇, были изготовлены в прессе типа Уокера с несколькими наковальнями. Стехиометрические количества Dy ₂ O ₃ и GeO ₂ тщательно измельчали, оборачивали в золотую фольгу, сжимали до 7 ГПа и нагревали до 1000 ° С. Уточнение Ритвельдом порошковой рентгенограммы подтвердило гранецентрированную кубическую пространственную группу (Fd-3m, № 227) и отсутствие тетрагонального пирогерманата. Параметр решетки при комнатной температуре был определен равным 9, 9290 (5) Å (рис. 2 (вставка)). Измерения в зависимости от температуры и поля намагниченности подтвердили редкоземельный магнитный момент moment 10 мкБ и постоянную Кюри – Вейсса 0, 0 К. Теплоемкость была измерена с использованием метода тепловой релаксации от 0, 34 до 25 К. Вклад решетки был вычтен из измеренной удельной теплоемкости, чтобы выявить магнитный вклад. Энергия u ( T ) была найдена путем численного интегрирования измеренной удельной теплоты.

2. Симметрия уравнений Максвелла

Сформулированные Максвеллом уравнения классической электродинамики связывают электрическое и магнитное поле с движением заряженных частиц. Эти уравнения почти симметричны относительно электричества и магнетизма. Они могут быть сделаны полностью симметричными, если в дополнение к электрическому заряду и току ввести некий магнитный заряд ρ_m и магнитный ток :

Название	Без магнитных монополей	С магнитными монополями
Теорема Гаусса:
Магнитный закон Гаусса
Закон индукции Фарадея:
Закон Ампера (с током смещения):

При этом изменённые уравнения из правой колонки переходят в классические уравнения при подстановке ρ_m = 0 и , то есть если в рассматриваемой области пространства отсутствуют магнитные заряды. Таким образом можно создать систему уравнений Максвелла с учетом существования магнитных зарядов, при этом классические уравнения просто отражают тот факт, что обычно магнитные заряды не наблюдаются.

Если магнитные заряды существуют, то существование магнитных токов приведёт к существенным поправкам уравнений Максвелла, которые можно наблюдать на макроскопических масштабах.

В новой форме уравнений Максвелла возникают трудности математического описания при помощи вектор-потенциала. При наличии и магнитных и электрических зарядов электромагнитное поле не может быть описано при помощи вектор-потенциала , непрерывного во всём пространстве. Поэтому при наличии магнитных зарядов уравнения движения заряженных частиц не выводятся из вариационного принципа наименьшего действия. В классической электродинамике это не приводит к принципиальным трудностям (хотя и делает теорию несколько менее красивой), но квантовую динамику невозможно сформулировать вне рамок гамильтонова или лагранжева формализма.

6. Попытки найти монополь

Неоднократные попытки экспериментального обнаружения магнитного монополя не увенчались успехом. Особенно интенсивно поиски магнитного монополя космического происхождения проводились с начала 80-х годов XX века. Эксперименты можно разделить на несколько групп.

1. Магнитный монополь можно обнаружить непосредственно по связанному с ним магнитному потоку. Прохождение магнитного заряда ng сквозь сверхпроводящий контур изменит поток на 2πΦ, где  — квант магнитного потока, и явление электромагнитной индукции приведёт к скачку тока в контуре, который может быть измерен с помощью сверхпроводящего квантового интерферометра (так называемого «СКВИДа» — SQUID, англ. Superconducting Quantum Interference Detector). По теоретическим оценкам, плотность монополей настолько мала, что через один прибор пролетает один монополь в год: в среднем один монополь приходится на 1029 нуклонов. Несмотря на то, что были зафиксированы обнадёживающие события, в частности событие Бласа Кабреры (Blas Cabrera) в ночь на 14 февраля 1982 года (иногда в шутку называемый «монополем Дня Святого Валентина»), эти эксперименты не удалось воспроизвести, и существование монополей не было установлено.
2. Тяжёлый магнитный монополь должен обладать высокой проникающей способностью и создавать на своём пути сильную ионизацию. Поэтому для поисков магнитного монополя использовались подземные детекторы, сооружённые для изучения потоков космических нейтрино и поисков распада протона. Вероятность того, что пролетающий монополь родит фотон в детекторе, является убывающей функцией его массы. Недавние эксперименты на Тэватроне показали, что монополи с массами менее 600 и 900 ГэВ в зависимости от спина не существуют, в то время как верхний предел их массы равен 1017 ГэВ.
3. Проводились также поиски магнитных монополей, захваченных в магнитных рудах земного и внеземного (метеориты, Луна) происхождения, а также треков, оставленных ими в слюде, заключённой в древних земных породах. Ставились и опыты с целью обнаружения процессов рождения магнитных монополей при столкновениях частиц высокой энергии на ускорителях, однако массы таких магнитных монополей, естественно, ограничены энергией, доступной на современных ускорителях. Наиболее сильное ограничение на возможное число магнитных монополей в космическом пространстве дают соображения, связанные с наличием галактических магнитных полей, так как монополи ускорялись бы в этих полях, отбирая тем самым энергию у их источников, что приводило бы к ослаблению полей со временем. Численная оценка этого ограничения зависит от ряда предположений, но едва ли поток космических магнитных монополей в единичном телесном угле может превосходить 10−12 м−2 ср−1.

6.1. Магнитные «квазимонополи»

В некоторых системах в физике конденсированного вещества могут существовать структуры, напоминающие магнитный монополь — трубки магнитного потока (flux tubes). Концы магнитной трубки образуют магнитный диполь, однако поскольку их движение независимо, во многих случаях они могут приближённо рассматриваться как независимые квазичастицы-монополи.

В сентябре 2009 года сразу несколько независимых исследовательских групп объявило об обнаружении в твёрдом теле (спиновом льду из титаната диспрозия Dy₂Ti₂O₇) квазичастиц, имитирующих магнитные монополи (то есть выглядящих как монополи на расстояниях, значительно превышающих постоянную кристаллической решётки). В некоторых СМИ и научно-популярных публикациях это наблюдение было подано как обнаружение магнитных монополей.

Однако эти явления не связаны и, согласно сообщению в Physics World, магнитные монополи, обнаруженные в «спиновом льду», своим происхождением отличаются от фундаментальных монополей, предсказываемых теорией Дирака.

Обнаруженные «монополи» являются квазичастицами (магнитные силовые линии, входящие в одну из таких квазичастиц, остаются замкнутыми, проходя сквозь тонкий «шнур», соединяющий две такие квазичастицы, каждая из которых в этом смысле не представляет собой изолированный магнитный заряд), а не элементарными частицами, поэтому данное открытие не произвело переворота в физике элементарных частиц. Тем не менее «квазимонополи» интересны сами по себе и являются объектом интенсивных исследований. Теоретически подобные образования могут существовать не только в спиновом льду, но также в конденсате Бозе — Эйнштейна.

Техническое описание

В 1935 году Линус Полинг заметил, что атомы водорода в водяном льду, как ожидается, останутся неупорядоченными даже при абсолютном нуле . То есть даже при охлаждении до нулевой температуры ожидается , что водяной лед будет иметь остаточную энтропию , то есть внутреннюю хаотичность. Это связано с тем, что гексагональная кристаллическая структура обычного водяного льда содержит атомы кислорода с четырьмя соседними атомами водорода . Во льду для каждого атома кислорода два соседних атома водорода находятся рядом (образуя традиционную молекулу H ₂ O ), а два — дальше (являясь атомами водорода двух соседних молекул воды). Полинг отметил, что количество конфигураций, соответствующих этому правилу льда «два-близко, два-далеко», растет экспоненциально с увеличением размера системы, и, следовательно, энтропия льда при нулевой температуре должна была быть значительной . Выводы Полинга были подтверждены измерениями удельной теплоемкости , хотя чистые кристаллы водяного льда создать особенно сложно.

Рис. 2. Участок решетки пирохлора из тетраэдров с угловой связью. Магнитные ионы (темно-синие сферы) сидят на сети тетраэдров, соединенных в своих вершинах. Другие атомы (например, Ti и O), образующие кристаллическую структуру пирохлора, не отображаются. Магнитные моменты (голубые стрелки) подчиняются правилу спинового льда «два входа — два выхода» для всей решетки. Таким образом, система находится в состоянии спинового льда.

Спин-льды — это материалы, которые состоят из правильных тетраэдров магнитных ионов с угловыми связями , каждый из которых имеет ненулевой магнитный момент , часто сокращенный до « спина », который в своем низкоэнергетическом состоянии должен удовлетворять условию «два-в-два». -out «правило на каждом тетраэдре, образующем кристаллическую структуру (см. рисунок 2). Это очень похоже на правило «два — близко, два — далеко» в водяном льду (см. Рис. 1). Так же, как Полинг показал, что правило льда приводит к большой энтропии в водяном льду, то же самое делает правило «два входа — два выхода» в системах спинового льда — они обладают такими же остаточными энтропийными свойствами, что и водяной лед. Как бы то ни было, в зависимости от конкретного материала спинового льда, как правило, намного легче создать большие монокристаллы материалов спинового льда, чем кристаллы водяного льда. Кроме того, легкость создания взаимодействия магнитных моментов с внешним магнитным полем в системе спинового льда делает спиновые льды более подходящими, чем водяной лед, для исследования того, как на остаточную энтропию могут влиять внешние воздействия.

В то время как Филип Андерсон уже отметил в 1956 году связь между проблемой фрустрированного антиферромагнетика Изинга на ( ) решетке тетраэдров с общими углами и проблемой водяного льда Полинга, настоящие материалы спинового льда были открыты только сорок лет спустя. Первыми материалами, идентифицированными как спиновые льды, были Dy ₂ Ti ₂ O ₇ ( титанат диспрозия ), Ho ₂ Ti ₂ O ₇ (титанат гольмия). Кроме того, были получены убедительные доказательства того, что Dy ₂ Sn ₂ O ₇ ( станнат диспрозия ) и Ho ₂ Sn ₂ O ₇ ( станнат гольмия ) являются прядильными льдами. Эти четыре соединения принадлежат к семейству редкоземельных оксидов пирохлора. CdEr ₂ Se ₄ , шпинель, в которой магнитные ионы Er 3+ сидят на тетраэдрах с угловыми связями, также демонстрирует поведение спинового льда.

Материалы спинового льда характеризуются случайным беспорядком в ориентации момента магнитных ионов , даже когда материал находится при очень низких температурах . Измерения магнитной восприимчивости на переменном токе (AC) обнаруживают доказательства динамического замораживания магнитных моментов, поскольку температура несколько понижается ниже температуры, при которой удельная теплоемкость достигает максимума. Широкий максимум теплоемкости не соответствует фазовому переходу. Скорее, температура, при которой происходит максимум, около 1 К в Dy ₂ Ti ₂ O ₇ , сигнализирует о быстром изменении числа тетраэдров, где нарушается правило «два входа — два выхода». Тетраэдры, в которых правило нарушается, — это участки, в которых находятся вышеупомянутые монополи.

4. Модель ‘т Хоофта — Полякова

В 1974 А. М. Поляков и Герард ‘т Хоофт (G. ‘t Hooft) независимо обнаружили, что существование магнитного монополя не только возможно, но и обязательно в полевых теориях определённого класса. В моделях великого объединения, рассматривающих симметрию относительно фазовых преобразований волновых функций заряженных частиц как составную часть более широкой неабелевой калибровочной симметрии, электромагнитное поле связано с мультиплетом заряженных калибровочных полей X с большими массами (эти массы возникают при спонтанном нарушении симметрии). Для некоторых калибровочных групп симметрии существуют устойчивые конфигурации полей X, локализованные в области размером и создающие вне этой области сферически симметричное магнитное поле. Существование таких конфигураций зависит от топологических свойств калибровочной группы, точнее, от того, каким образом в неё вложена подгруппа симметрии, сохранившейся после спонтанного нарушения. Стабильность этих магнитных монополей определяется особым поведением полей на больших расстояниях от центра. Масса магнитного монополя M_m может быть вычислена, она зависит от конкретной полевой модели, однако во всяком случае должна быть большой, (по оценке, для широкого класса моделей ). Эти магнитные монополи могли бы рождаться в горячей Вселенной вскоре после Большого Взрыва при фазовом переходе, связанном со спонтанным нарушением симметрии и возникновением отличных от нуля однородных скалярных полей в вакууме. Количество рождающихся магнитных монополей определяется процессом развития Вселенной на ранней стадии, поэтому по их отсутствию в настоящее время можно судить об этом процессе. Одно из объяснений того, что реликтовые магнитные монополи не обнаружены, даётся теорией раздувающейся Вселенной (инфляции). Магнитные монополи ‘т Хоофта — Полякова обладают некоторыми необычными свойствами, благодаря которым их было бы легко обнаружить. В частности, взаимодействие с магнитным монополем может стимулировать распад нуклона, предсказываемый некоторыми моделями великого объединения, то есть выступать в качестве катализатора такого распада.

5. Основные физические свойства

5.1. Заряд магнитного монополя

Размерность заряда магнитного монополя совпадает с размерностью электрического заряда в системе СГС:

где c — скорость света в вакууме,  — постоянная Планка и e — элементарный заряд.

В системе СИ размерности магнитного и электрического зарядов различны:

где h — постоянная Планка.

5.2. Константа связи монополя

Известно, что электрические заряды имеют достаточно малую константу связи (т. н. постоянную тонкой структуры). В системе СГС она имеет следующее значение:

В системе СИ мы имеем более громоздкое выражение:

где ε_E — диэлектрическая постоянная.

Аналогичным образом можно ввести и магнитную константу связи для системы СГС:

Для системы СИ имеет место выражение:

где μ_E — магнитная постоянная вакуума. Здесь следует отметить, что магнитная константа значительно больше единицы и поэтому использование пертурбативных методов в квантовой электродинамике для магнитных зарядов не предоставляется возможным.

5.3. Масса монополя

Теория Дирака не предсказывает «массу магнитного монополя». Поэтому в настоящее время отсутствует единое мнение по оценке массы монополя (эксперимент только указывает на нижнюю границу). Здесь также можно отметить, что значение массы электрона является чисто экспериментальным фактом и не предсказывается существующими теориями.

5.3.1. Нижняя оценка массы монополя

Нижнюю оценку для массы монополя можно оценить исходя из классического радиуса электрона (система СИ):

где λ — комптоновская длина волны электрона, m — масса электрона

Аналогичным образом можно ввести значение для классического радиуса магнитного монополя (система СИ):

где m_D — масса монополя. Таким образом, приравнивая классические радиусы, можно получить нижнюю оценку массы монополя:

Анализ теплоемкости

Чтобы рассчитать удельную теплоемкость, для каждого узла решетки алмаза была записана энергия u = | ν | х, где х — число монополей на узел решетки:

, Здесь ν _DH — стандартная поправка Дебая-Хюккеля к химическому потенциалу (связанная с коэффициентом электрохимической активности): | ν _DH | / k _B T = l _T / ( l _D + a ), где l _T = μ Q 2 / (8 πk _B T ), длина Бьеррума,

— длина Дебая, а V _d — объем на узел алмазной решетки (подробное обсуждение этих величин см. в ссылке 23). Используя эти уравнения, x и l _D определялись самосогласованно, а затем удельная теплоемкость определялась путем дифференцирования u .

Чтобы включить димеры заряда, мы рассматривали их как пары ближних соседей, что подходит для решетки 26 . Их химический потенциал ν _d = 2 | ν | — μ Q 2 / (4 πa ), давая число пар на узел решетки алмаза: x _B ≈2exp− | ν _d | / ( k _B T ). Поправка Дебая-Хюккеля была изменена, чтобы избежать двойного учета этих пар следующим образом: ν _DH / ( k _B T ) → l _T / ( l _D +2 a ). Затем энергия была рассчитана как: u = | ν _д | х _B + | ν | х, который был сравнен с измеренным u ( T ).

Эти методы были всесторонне проверены и продемонстрировали, что они обеспечивают надежный анализ данных по удельной теплоемкости материалов с ледяным покровом. Они были использованы для оценки кривых на рисунках 1, 3 и 4. На рисунке 1 химические потенциалы: 3, 35 К (DyGe), 4, 35 К (DyTi), 5, 5 К (HoGe) и 5, 8 К (HoTi) в очевидная запись; для материалов Ho это только приблизительные оценки из-за сложности точной изоляции электронной удельной теплоемкости от ядерного компонента 9 .

Теория Дебая-Хюккеля

На рисунке 3 мы показываем измеренные значения c _m / T, построенные в зависимости от температуры и соответствующие теории Дебая-Хюккеля с химическим потенциалом монополя ν = (3, 35 ± 0, 05) K. Используемый нами метод был разработан для расширения теории Дебая-Хюккеля до хорошее приближение к высокотемпературному режиму; при применении к Dy ₂ Ti ₂ O ₇ этот метод дает такое же хорошее соответствие c _m ( T ) / T с химическим потенциалом ожидаемой величины. Он основан на сопоставлении системы с решеточным газом с исключением сайтов. Считается, что решеточный газ имеет изменяющийся при температуре химический потенциал, равный сумме истинного химического потенциала, как определено в работе. 28 и стандартная кулоновская поправка Дебая-Хюккеля к химическому потенциалу 30 . Без последней поправки предсказанная удельная теплоемкость (пунктирная линия на рис. 3) хорошо описывает экспериментальные данные в пределе высоких и низких температур, подчеркивая, что этот подход является надежным методом получения экспериментальной оценки химического потенциала монополя, который существенно не смещены ограничениями теории Дебая-Хюккеля. Попутно отметим, что происхождение приблизительного коллапса экспериментальных данных и расчета Дебая-Хюккеля на модель идеального решеточного газа при высокой температуре имеет другое происхождение, чем при низкой температуре. В последнем случае монопольный газ достаточно разбавлен, чтобы можно было пренебрегать взаимодействиями, тогда как в первом случае плотный и взаимодействующий монопольный газ воспроизводит кажущееся поведение идеального газа, что приводит к сильному кулоновскому экранированию.

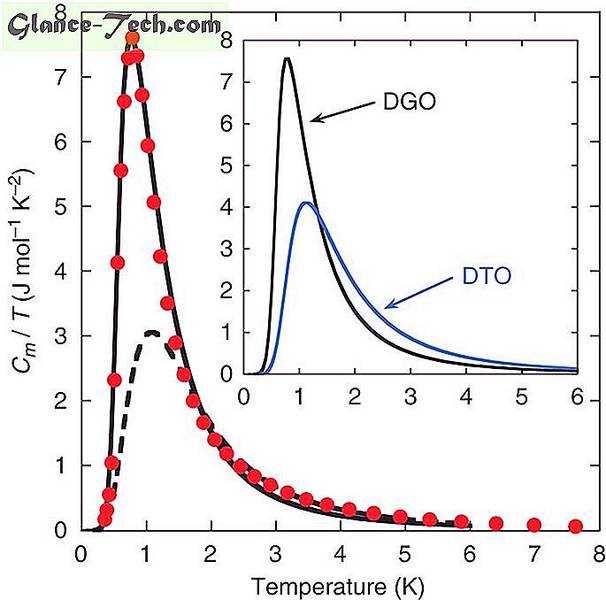
Основная фигура: модифицированная теория Дебая-Хюккеля (черная линия), с монопольным химическим потенциалом ν = 3, 35 (5) K, единственным регулируемым параметром, дает превосходное описание экспериментальной магнитной теплоемкости Dy ₂ Ge ₂ O ₇ (баллы), Пунктирная черная линия показывает теплоемкость идеального решетчатого газа с исключением на месте с тем же химическим потенциалом. Эта модель хорошо описывает данные при низких температурах, когда кулоновскими взаимодействиями можно пренебречь, и при высоких температурах, где взаимодействия сильно экранированы. Врезка: влияние изменения химического потенциала от -3, 35 К (соответствует Dy ₂ Ge ₂ O ₇ (DGO)) до -4, 35 К (соответствует Dy ₂ Ti ₂ O ₇ (DTO)).

Изображение в полном размере

В качестве дальнейшего теста на согласованность, мы можем использовать наше подогнанное значение ν, чтобы получить значение эффективной константы связи ближнего соседа, J _eff, в соответствии с соотношением, обсужденным в работе. 16, а затем сравните это с J _eff, оцененным по температуре максимума удельной теплоемкости, как обсуждалось в работе. 31. Результатом являются J _eff = (0, 62 ± 0, 1) K, (0, 60 ± 0, 1) K, соответственно, оценки, которые равны в пределах ошибки эксперимента. Для Dy ₂ Ti ₂ O ₇ соответствующее значение равно J _eff ≈1, 1 К, что примерно в два раза больше. Большая разница объясняется более отрицательным (антиферромагнитным) обменным вкладом в спин-спиновое взаимодействие в Dy ₂ Ge ₂ O _7, который противодействует положительному (ферромагнитному) дипольному взаимодействию, что почти одинаково в двух соединениях.

Энтропия Полинга

Фаза чистого кубического Dy ₂ Ge ₂ O ₇ и Ho ₂ Ge ₂ O ₇ были приготовлены и охарактеризованы, как описано в методах. Здесь мы подробно опишем наши результаты только для соединения Dy и просто отметим, что мы выполнили аналогичную характеристику соединения Ho, которое оказалось менее интересным в данном контексте, так как оно имеет более типичный химический потенциал (рис. 1). Магнитная энтропия, определенная путем интегрирования удельной теплоты, деленной на температуру (см / т ), показана на рисунке 2, где остаточная энтропия Полинга, ожидаемая для спинового льда 8, очень хорошо воспроизводится. Магнитометрические измерения на Dy ₂ Ge ₂ O ₇ показали, что этот материал обладает магнитным моментом, очень похожим на Dy ₂ Ti ₂ O ₇ . Имея незначительную погрешность, мы впредь будем считать, что магнитный момент на Dy одинаков в двух материалах (9, 87 мкБ ) 15 .

3. Дираковский монополь

Поль Дирак создал квантовую теорию взаимодействия электрического заряда e с магнитным зарядом g, которая применима при условии: , где n — целое число. Таким образом, магнитный заряд частицы должен быть кратен элементарному магнитному заряду , где e — элементарный электрический заряд.

Примечательно обратное утверждение: существование магнитного заряда не противоречит стандартной квантовой механике только в том случае, если электрические заряды всех частиц квантуются. (Таким образом, существование в природе хотя бы одного магнитного монополя с определённым зарядом объяснило бы наблюдаемую на опыте кратность электрических зарядов частиц величине e; магнитный заряд при этом тоже с необходимостью квантовался бы.)

Условие квантования Дирака обобщается на взаимодействие двух частиц, каждая из которых обладает как электрическим, так и магнитным зарядом (такие частицы называется дионами)

(В используемой системе единиц e и g имеют одинаковую размерность, причём заряд e фиксирован соотношением .)

В нерелятивистском приближении сила, действующая на дион 1 с координатами r и скоростью v со стороны диона 2, закреплённого в начале координат, равна

Отметим, что входящие в эту формулу комбинации зарядов инвариантны относительно дуального преобразования.