Исследование фракталов: ковер серпинского

Комплексные числа

Комплексное число — это число, состоящее из двух частей — действительной и мнимой, то есть формальная сумма x + iy (x и y здесь — вещественные числа). i — это т.н. мнимая единица, то есть то есть число, удовлетворяющее уравнению
i^2 = -1. Над комплексными числами определены основные математические операции — сложение, умножение, деление, вычитание (не определена только операция сравнения). Для отображения комплексных чисел часто используется геометрическое представление — на плоскости (ее называют комплексной) по оси абсцисс откладывают действительную часть, а по оси ординат — мнимую, при этом комплексному числу будет соответствовать точка с декартовыми координатами x и y.

Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f (z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жулиа для функции f (z).

Броуновское движение на ковре Серпинского [ править ]

Тема броуновского движения на ковре Серпинского вызывает интерес в последние годы. Мартин Барлоу и Ричард Басс показали, что случайное блуждание по ковру Серпинского распространяется медленнее, чем неограниченное случайное блуждание по плоскости. Последний достигает среднего расстояния, пропорционального √ n, после n шагов, но случайное блуждание по дискретному ковру Серпинского достигает только среднего расстояния, пропорционального β √ n для некоторого β > 2 . Они также показали, что это случайное блуждание удовлетворяет более сильному большому отклонениюнеравенства (так называемые «субгауссовские неравенства») и что оно удовлетворяет эллиптическому неравенству Гарнака, не удовлетворяя параболическому неравенству . Существование такого примера долгие годы оставалось открытой проблемой.

Математические фракталы

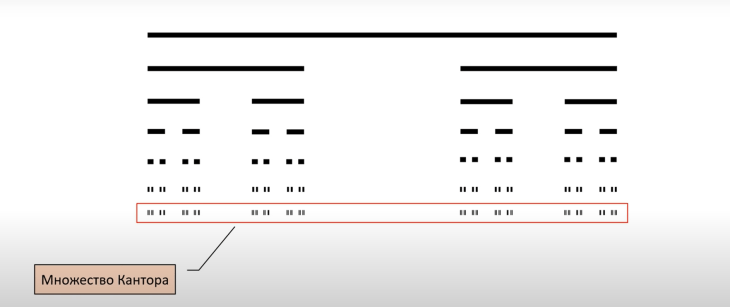
Для лучшего понимания определения можно вспомнить простые примеры математических фракталов. Например, множество Кантора – это бесконечная череда отрезков, из которых изъяли среднюю часть. Понять, что это такое проще, посмотрев на рисунок. В итоге мы получаем множество, которое при масштабировании переходит само в себя.

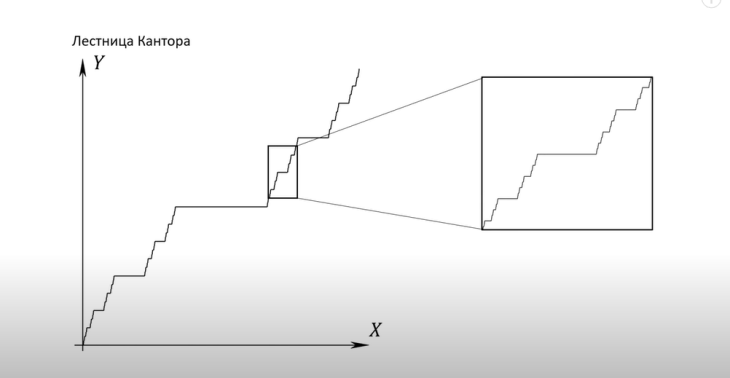
Еще один пример – это лестница Кантора. Это функция, которая строится из одинаковых повторяющихся элементов. Она представляет собой непрерывный график. При масштабировании ее отдельных частей получается она сама целиком.

Треугольник Серпинского строится путем построения в каждом элементе новой аналогичной геометрической фигуры. В результате такого построения получается очень красивое множество, состоящее из самоподобных треугольников.

Сито Уоллиса [ править ]

Третья итерация сита Уоллиса

Вариант ковра Серпинского, называемый решето Уоллиса , начинается таким же образом, когда единичный квадрат делится на девять меньших квадратов и удаляется середина из них. На следующем уровне подразделения он делит каждый из квадратов на 25 меньших квадратов и удаляет средний, и продолжается на i- м шаге, разделяя каждый квадрат на (2 i + 1) 2 ( нечетные квадраты ) квадратов меньшего размера и удаления среднего.

По произведению Уоллиса площадь результирующего множества равнаπ4, в отличие от стандартного ковра Серпинского, который имеет нулевую предельную площадь.

Однако по результатам Уайберна, упомянутым выше, мы видим, что сито Уоллиса гомеоморфно ковру Серпинского. В частности, его интерьер по-прежнему пуст.

Области применения

Сферы применения фракталов очень многочисленны, в частности можно процитировать:

• в биологии — распределение структур растений, бактерий, листьев, ветвей деревьев …
• в геологии , изучении рельефа, побережьях и водотоках, структурах горных пород, сходах лавин …
• в палеонтологии — степенной закон появления и исчезновения видов
• в морфологии животных, строении беспозвоночных, перьях птиц …
• в медицине строение легких, кишечника, сердцебиение
• в метеорологии , облака, вихрь , льдина , волны-убийцы , турбулентность , структура молнии
• в вулканологии , предсказании извержений вулканов , землетрясений
• в астрономии с описанием строения Вселенной , кратеров на Луне , распределения экзопланет и галактик …
• в гуманитарных науках , эволюция демографии
• в области экономики и финансов , (неточная) попытка предсказать крах фондового рынка (» мультифрактальная  » теория  )
• в электронике , широкополосные антенны для мобильных телефонов
• в городской географии , для анализа городских форм
• в градостроительной и общественно-политической сферах
  
• в искусстве , графике, конечно, но также в литературе , музыке , кино …

Все эти поля — и многие другие — могут извлечь выгоду из описания и моделирования связанных явлений во фрактальных терминах.

Модель начинает развиваться частности, в финансах, где фрактальный подход Мандельброта подходит для волатильных рынков. Некоторые компании используют модель, которая определяет математические повторения для прогнозирования определенных краткосрочных ценовых движений. Этот систематический подход основан на волатильности и ускорении торговли ценными бумагами с целью проверки тенденций. Таким образом, в модели сразу же регистрируется ожидание изменений: если изменение имеет достаточную величину, это позволяет, например, открыть короткую позицию («короткую» позицию, то есть короткую продажу , спекулирующую на нижней стороне. рынок.

Промышленное использование

Блейн удельная площадь поверхности : тонина помола из цемента выражается в терминах удельной площади поверхности (см ² / г) и измеряется Blaine методом , известным как воздушной проницаемости , используя закон Дарси , и права по Козени-Кармана , который установил что на прохождение жидкости через слой гранул влияет удельная площадь поверхности гранул.

Таким образом, вычисляя время, которое требуется сжатому газу для прохождения через заданный объем гранул, из него выводят площадь поверхности гранул. Чем мельче шлифовка, тем больше расчетная поверхность.

Поскольку этот опыт происходит в определенном объеме, можно представить себе получение бесконечно развитой поверхности путем все более и более тонкого измельчения цемента. Это промышленное использование модели, объясненной фрактальной математикой (объект размерности конечной меры, ограниченный границей измерения , меры, стремящейся к бесконечности).
нет{\ displaystyle n}нет-1{\ displaystyle n-1}

Информатика

• Fractint — это бесплатное программное обеспечение для рисования многих типов фракталов.
• Sterling — бесплатный генератор фракталов для Windows.
• XaoS — это бесплатное программное обеспечение, позволяющее как техническое, так и поэтическое открытие фракталов.
• FractaNep — это бесплатное программное обеспечение для построения множеств Мандельброта, Джулии и Ньютона (совместимо с Windows ).
• Qosmic — это программное обеспечение, предназначенное для создания фрактального пламени, визуализация которого генерируется алгоритмически.
• Компьютерные методы расчета
  • Система итерационных функций (IFS).
  • Игра хаос
  • Система Линденмайера или L-система .
  • Топологические методы.
  • Алгоритм алмаз-квадрат

Фракталы вокруг нас

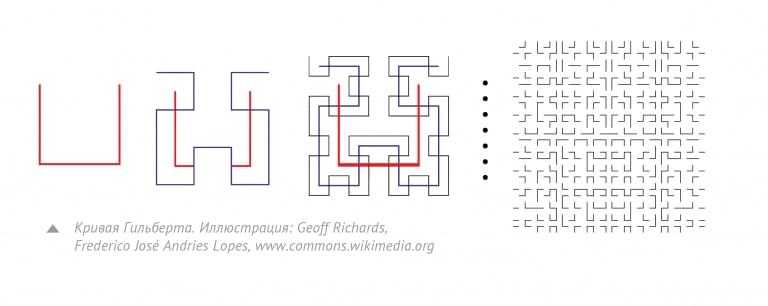
Например, одно из свойств фракталов основано на их способности иметь дробную размерность. Рассмотрим в качестве примера необычную кривую Гильберта с размерностью, очень близкой к 2, и нарисуем ее на плоскости. Она будет настолько извилистой, что полностью займет всю предоставленную ей плоскость, при этом оставаясь кривой с бесконечной длиной. Аналогично можно представить объемную структуру с небольшим объемом и бесконечной площадью – это человеческие легкие. Способность поглощать кислород напрямую зависит от площади дыхательной поверхности легких, но при этом они должны занимать относительно небольшой объем. Именно поэтому небольшие человеческие легкие имеют дыхательную поверхность большую, чем стандартный теннисный корт.

Теорию фракталов используют в материаловедении. Шероховатости и неровности, остающиеся на поверхности любого металла после его полировки или изготовления, имеют фрактальную природу. И более того, по ним можно предсказать прочностные характеристики металла – существует прямая зависимость между фрактальной размерностью и энергией, необходимой для разрушения металла. Аналогичные результаты были в исследованиях полимеров. Оказалось, что полимерные цепочки образуют сложные и запутанные структуры, которые определяют ключевые показатели полимеров. И эти запутанные цепочки – тоже фракталы!

Отдельное развитие получили алгоритмы для генерации фракталов. Часть из них придумали еще в XIX веке, другие появились, когда возникла теория фракталов. Вместе они стали основой раздела в искусстве, посвященного фрактальным узорам. Вскоре выяснилось, что можно генерировать компьютерную графику при помощи фракталов. Особенно актуально это оказалось для биологических структур: деревьев и растений. У капусты Романеско, например, невооруженным глазом видна фрактальная структура.

Капуста романеско, www.fr.freepik.com
алгоритмы фрактального сжатия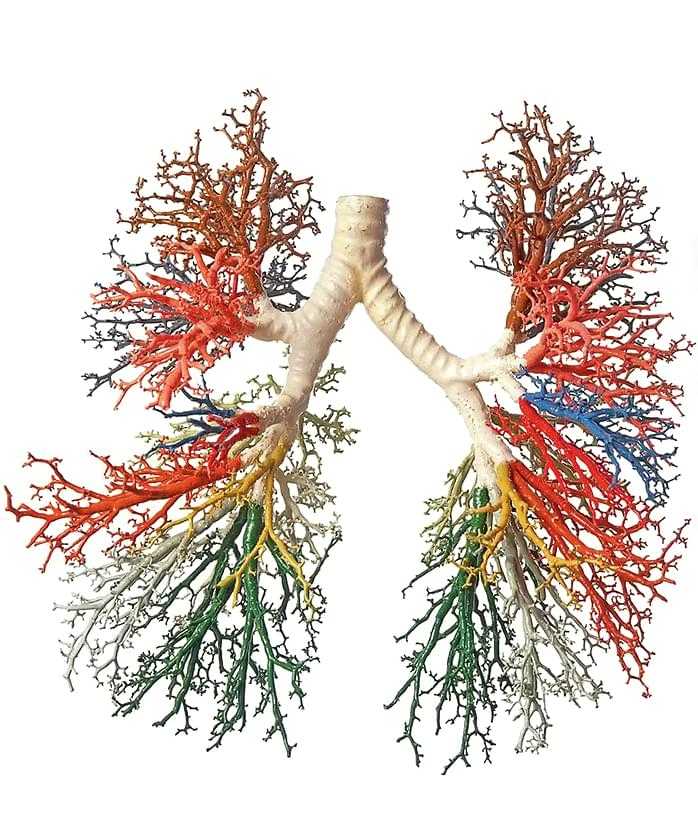«Дерево» бронхов. Фото: Dorling Kindersley/uig, www.fineartamerica.com Сечение губки Менгера. Иллюстрация: Cmglee, commons.wikimedia.org

Геометрия и алгебра

Изучение фракталов на рубеже XIX и XX веков носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс строит пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.

Другой класс — динамические (алгебраические) фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный мемуар Жулиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жулиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жулиа среди математиков того времени, о ней довольно быстро забыли

Вновь внимание к ней обратилось лишь полвека спустя с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов

Что такое фрактал

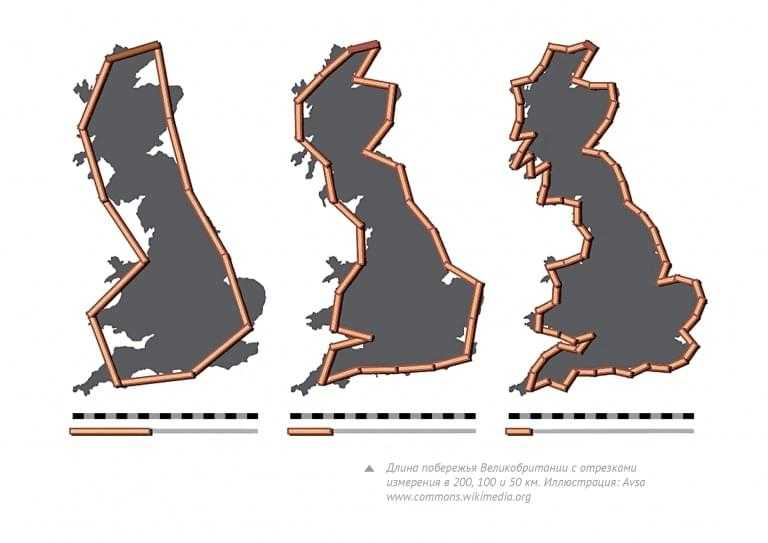
Предположим, что нам понадобилось измерить длину побережья какой-нибудь страны, например, Великобритании. Обычный метод – последовательно соединять две точки побережья линейкой на географическом атласе. Так же думал и английский ученый Льюис Фрай Ричардсон. Но, в отличие от других исследователей, он решил взять линейку покороче и измерить длину еще раз. И еще. И еще. И в каждом случае у него получалась разная длина! Казалось бы, здесь явно закралась ошибка. Однако, если мы внимательно посмотрим на изображение побережья Великобритании, то увидим, что Ричардсон был прав в своих подсчетах.

Длина измеряемой кривой зависит от масштаба измерений. И вот тут мы и подходим вплотную к понятию фрактала. Для обычной кривой при бесконечном уменьшении масштаба измерений ее длина станет постоянной. Например, для окружности таким образом можно получить формулу длины L = 2pR. Но длина побережья при постоянном уменьшении линейки будет неограниченно возрастать – это называется «парадоксом береговой линии», и именно с него началось научное изучение фракталов.

Если рассмотреть этот вопрос с физической точки зрения, то может показаться, что такое невозможно. Действительно, для реального, физического объекта мы не сможем бесконечно уменьшать масштаб измерений – рано или поздно мы дойдем до размеров атома. Однако из этого логичного рассуждения не следует невозможность существования фракталов – оно лишь показывает, что каждый объект обладает фрактальными свойствами лишь до определенного момента. И только математические объекты являются фракталами в полной мере и при любых измерениях. Из-за этой запутанности и сложности фракталов ученые обнаружили их как математический объект лишь во второй половине XX века. Хотя из примера с береговой линией очевидно, что они существовали и до этого, но только в 1975 году французский математик Бенуа Мандельброт написал книгу о фракталах и фактически основал теорию фракталов в недавно возникшей области науки – теории хаоса.

Однако еще до выхода книги, в 1967 году в журнале Science была опубликована его статья «How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension» о парадоксе береговой линии. В статье ни разу не встречается слово «фрактал», хотя именно она считается стартовой точкой для фрактальной геометрии. Мандельброт решает этот парадокс удивительным образом – он заявляет, что нельзя говорить о таком понятии, как «длина береговой линии», в привычном нам понимании. Чтобы доказать свое утверждение, он вводит ключевое для теории фракталов понятие фрактальной размерности. Самое странное в ней то, что она не является целой!

В математике размерностью обычно называют топологическую размерность, которая просто-напросто соответствует количеству измерений предмета. Так, куб имеет три измерения – длину, ширину и высоту, следовательно, его размерность равна трем. А линия на бумаге имеет только длину, и ее размерность равна единице. Поэтому на первый взгляд кажется невозможным представить предмет с нецелой размерностью. Какой объект может иметь размерность 1,26? А ведь его описали еще в 1904 году и более полувека попросту не обращали на него внимания, считая забавной игрушкой. Это снежинка Коха, представляющая собой замкнутую кривую с простейшим алгоритмом построения, из которого ясно, что ее длина в привычном нам понимании бесконечна. Математики ввели для такой нецелой размерности отдельный термин – размерность Хаусдорфа-Безиковича.

Также можно заметить схожесть этой снежинки с изрезанной береговой линией – каждый ее фрагмент в крупном масштабе подобен ее же более мелкому фрагменту. Это свойство называется самоподобием – оно ключевое для всех фракталов. Из аналогии с береговой линией мы можем получить интуитивное понимание нецелой размерности – ее можно описать как «степень изрезанности кривой».

Губка Менгера. Иллюстрация: Niabot, www.de.wikipedia.org

Из-за неоднозначного понимания фракталов существует целое множество их определений. Наиболее общее, предложенное Мандельбротом, гласит, что фракталом называют структуру, состоящую из частей, которые в каком-то смысле подобны целому. При этом фрактал не обязательно должен быть кривой, как в предыдущих примерах, – это может быть как плоская, так и объемная фигура. Например, фракталами являются ковер Серпинского или губка Менгера.

Характеристики

Анимированная конструкция: кривая фон Коха .

Фрактальный объект обладает как минимум одной из следующих характеристик:

• его хаусдорфова размерность строго больше его топологической размерности . Эта характеристика обычно принимается как само определение фрактального объекта. Другими словами, ирригационная сеть — это развертывание линий («в 1D  »), которые предлагают характеристики, которые начинают вызывать поверхность («в 2D»). Поверхность легкого («в 2D  ») складывается в своего рода объем («в 3D  »). Пиктографически фракталы характеризуются нецелочисленным измерением. ( Мандельброт не считает это определение полностью удовлетворительным);
• он имеет аналогичные детали в произвольно малых или больших масштабах;
• он слишком неправильный, чтобы его можно было эффективно описать в традиционных геометрических терминах;
• оно точно или статистически автоподобно , то есть целое похоже на одну из своих частей.

Основные параметры при проектировании антенн

Существует несколько важных характеристик, которые следует учитывать при разработке антенны для конкретного устройства, а именно: частота и размер, направленность, особенности конструкции, особенности использования.

Частота и размер

Антенны, используемые для ВЧ, отличаются от антенн, используемых для УКВ и СВЧ. Длина волны различна на разных частотах, поэтому антенны должны быть разного размера, чтобы излучать сигналы на соответствующей длине волны. В качестве примера интересны антенны, работающие в микроволновом диапазоне, особенно на частотах 2,4 и 5 ГГц. На частоте 2,4 ГГц длина волны составляет 12,5 см, а при 5 ГГц — 6 см.

Направленность

Антенны могут быть всенаправленными, секторными или узконаправленными. Всенаправленные антенны излучают один и тот же сигнал по всей антенне по всем 360°. Наиболее популярными типами всенаправленных антенн являются дипольные и плоские. Излучение секторных антенн распространяется только в определенной области. Луч может охватывать сектор 180°или 60°. Узконаправленными называют антенны, в которых ширина луча намного меньше, чем в секторных антеннах. Они имеют самый высокий коэффициент усиления и поэтому используются для линий дальней связи. Это, например, волновые, параболические, логопериодические, зигзагообразные, синфазные и многие другие антенны.

Особенности конструкции

Антенны могут быть построены различными способами, начиная от простых проводов и заканчивая параболическими конструкциями. При рассмотрении антенн, подходящих для использования WLAN с частотой 2,4 ГГц, можно использовать классификацию, приведенную ниже.

Применение

Можно выделить две основные категории для применения антенн: базовые станции и связь типа точка-точка. Каждая из этих категорий предполагает применение антенн разных типов. Базовые станции должны обеспечивать доступ для многих устройств. Для них целесообразно использование всенаправленных или секторных антенн, охватывающих только определенную область. В случае соединений типа точка-точка, напротив, эффективным будет использование узконаправленных антенн.

Немного о размерностях.

В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы прикидываем длину дороги (250 м), узнаем площадь квартиры (78 м2) и ищем на наклейке объем бутылки пива (0.33 дм3). Это понятие вполне интуитивно ясно и, казалось бы, не требует разъяснения. Линия имеет размерность 1. Это означает, что, выбрав точку отсчета, мы можем любую точку на этой линии определить с помощью 1 числа — положительного или отрицательного. Причем это касается всех линий — окружность, квадрат, парабола и т.д.

Размерность 2 означает, что любую точку мы можем однозначно определить двумя числами. Не надо думать, что двумерный — значит плоский. Поверхность сферы тоже двумерна (ее можно определить с помощью двух значений — углов наподобие ширины и долготы).

Если смотреть с математической точки зрения, то размерность определяется следующим образом: для одномерных объектов — увеличение в два раза их линейного размера приводит к увеличению размеров (в данном случае длинны) в два раза
(2^1).

Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (например, площадь прямоугольника) в четыре раза
(2^2).

Для 3-х мерных объектов увеличение линейных размеров в два раза приводи к увеличению объема в восемь раз
(2^3) и так далее.

Таким образом, размерность D можно рассчитать исходя из зависимости увеличения «размера» объекта S от увеличения линейных размеров L. D=log(S)/log(L). Для линии D=log(2)/log(2)=1. Для плоскости D=log(4)/log(2)=2. Для объема D=log(8)/log(2)=3. Может быть немного запутано, но в общем-то несложно и понятно.

Зачем я это все рассказываю? А для того чтобы понять, как отделять фракталы от, скажем, колбасы. Попробуем посчитать размерность для кривой Пеано. Итак, у нас исходная линия, состоящая из трех отрезков длинны Х, заменяется на 9 отрезков втрое меньшей длинны. Таким образом, при увеличении минимального отрезка в 3 раза длина всей линии увеличивается в 9 раз и D=log(9)/log(3)=2 — двумерный объект!!!

Так вот, когда размерность фигуры получаемой из каких-то простейших объектов (отрезков) больше размерности этих объектов — мы имеем дело с фракталом.

Фракталы делятся на группы. Самые большие группы это:

Исторический

Многие примеры фракталов, такие как Коха снежинкой или ковер Serpinski были обнаружены в конце 19 — го  века, но Бенуа Мандельброт , который в 1975 году обратил внимание на эти объекты и их вездесущность в природе, создавая по этому поводу прилагательное «фрактал» из Латинский корень фрактус , что означает «сломанный», «неправильный», и окончание «-ал» присутствует в прилагательных «военно-морской» и «банальный» (множественное число: морские, банальные, фрактальные); затем употребление наложило существительное фрактал для обозначения фигуры или уравнения фрактальной геометрии.

Возможно, вам также будет интересно

Быстрое проникновение беспроводных технологий в самые разные сферы жизни и наше стремление постоянно быть на связи требуют большего количества антенн для передачи и приема радиочастотных сигналов. Оборудование связи становится все более доступным и компактным, и это требует не только небольших по размерам, но и по возможности недорогих антенн. В статье представлен краткий обзор ассортимента ант…

В статье рассматривается один из продуктов компании Sierra Wireless — GSM/GPRS встраиваемый модем. По мнению разработчиков, определяющими критериями выбора данного модуля являются его уровень надежности, простота исполнения и приемлемая стоимость. Изучив соответствующие характеристики и работая над информационной поддержкой GSM-модема WISMO, мы прогнозируем, что в ближайшее время эта модель…

ОАО «Мобильные ТелеСистемы» объявило о старте продаж в своей розничной сети компактного устройства персонального GPS-мониторинга «МТС-Трекер», открывающего широкому кругу абонентов доступ к навигационным сервисам МТС по определению местоположения людей и объектов.
«МТС-Трекер» — это мобильное устройство, которое принимает сигнал со спутников GPS, вычисляет координаты, скорость движения и …

Строительство [ править ]

Строительство ковра Серпинского начинается с квадрата . Квадрат разрезается на 9 конгруэнтных подквадратов в сетке 3 на 3, а центральный подквадрат удаляется. Затем та же процедура применяется рекурсивно к оставшимся 8 подквадратам до бесконечности . Это может быть реализовано как набор точек в единичном квадрате, координаты которого, записанные в базе три, не имеют цифры «1» в одной и той же позиции, используя представление бесконечно малых чисел . 0,1111⋯знак равно0,2{\ displaystyle 0,1111 \ dots = 0,2}

Процесс рекурсивного удаления квадратов является примером правила конечного подразделения .

Характеристики

Вариант Кривая Пеано со стертой средней линией образует ковер Серпинского

Площадь ковра равна нулю (в стандартном Мера Лебега ).

Доказательство: Обозначим как а_я область итерации я. потом а_{я + 1} = 89а_я. Так а_я = (89)я, который стремится к 0 при я уходит в бесконечность.

В интерьер ковра пусто.

Доказательство: Предположим от противного, что существует точка п в интерьере ковролин. Тогда есть квадрат с центром в п который полностью содержится в ковре. Этот квадрат содержит меньший квадрат, координаты которого кратны 13k для некоторых k. Но в этом квадрате должно быть отверстие в итерации. k, поэтому его нельзя вместить в ковер — противоречие.

В Хаусдорфово измерение ковра журнал 8журнал 3 ≈ 1.8928.

Серпинский продемонстрировал, что его ковер представляет собой универсальную плоскую кривую. То есть: ковер Серпинского — это компактное подмножество плоскости с Размер покрытия Лебега 1, и каждое подмножество плоскости с этими свойствами гомеоморфный к некоторому подмножеству ковра Серпинского.

Эта «универсальность» ковра Серпинского не является истинно универсальным свойством в смысле теории категорий: она не характеризует это пространство однозначно с точностью до гомеоморфизма. Например, непересекающееся соединение ковра Серпинского и круга также является универсальной плоской кривой. Однако в 1958 г. Гордон Уайберн однозначно характеризует ковер Серпинского следующим образом: любая кривая, которая локально связанный и не имеет «локальных точек разреза», гомеоморфен ковру Серпинского. Здесь местная точка отсечения это точка п для которого некоторая связная окрестность U из п имеет свойство, что U − {п} не связано. Так, например, любая точка окружности является локальной точкой разреза.

В той же статье Уайберн дал другую характеристику ковру Серпинского. Напомним, что континуум — непустое связное компактное метрическое пространство. Предполагать Икс — континуум, вложенный в плоскость. Предположим, что его дополнение на плоскости имеет счетное число компонент связности C₁, C₂, C₃, … и предположим:

• диаметр C_я стремится к нулю как я → ∞;
• граница C_я и граница C_j не пересекаются, если я ≠ j;
• граница C_я простая замкнутая кривая для каждого я;
• объединение границ множеств C_я плотно в Икс.

потом Икс гомеоморфен ковру Серпинского.

Ссылки [ править ]

1. ^ Allouche, Жан-Поль; Шаллит, Джеффри (2003). Автоматические последовательности: теория, приложения, обобщения . Издательство Кембриджского университета . стр.  405 -406. ISBN 978-0-521-82332-6. Zbl  1086.11015 .
2. ^ Semmes, Стивен (2001). Некоторые новые типы фрактальной геометрии . Оксфордские математические монографии. Издательство Оксфордского университета. п. 31. ISBN 0-19-850806-9. Zbl  0970.28001 .
3. ^ Серпинского, Wacław (1916). «Sur une Courbe cantorienne qui contient une image biunivoque et continue de toute courbe donnée». CR Acad. Sci. Париж (на французском). 162 : 629–632. ISSN 0001-4036 . JFM 46.0295.02 .
4. ^ Уайберн, Гордон (1958). «Топологическая характеристика кривой Серпинского» . Фонд. Математика . 45 : 320–324. DOI10,4064 / фм-45-1-320-324 .
5. ^ Барлоу, Мартин; Басс, Ричард, Броуновское движение и гармонический анализ на коврах Серпинского
6. ^ Слоан, Н. Дж. А. (ред.). «Последовательность A016754 (Нечетные квадраты: a (n) = (2n + 1) ^ 2. Также центрированные восьмиугольные числа.)» . Он -лайн энциклопедия целочисленных последовательностей . Фонд OEIS.
7. ^ Rummler, Hansklaus (1993). «Квадратная дырочка». Американский математический ежемесячник . 100 (9): 858–860. DOI10.2307 / 2324662 . JSTOR 2324662 . Руководство по ремонту 1247533 .
8. ^ Вайсштейн, Эрик В. «Сито Уоллис» . MathWorld .

Фрактал

Главное различие между хаосом и фракталом заключается в том, что первый является динамическим явлением, а фрактал статическим. Под динамическим свойством хаоса понимается непостоянное и непериодические изменения траекторий.

Фрактал — это геометрическая фигура, определенная часть которой повторяется снова и снова, отсюда проявляется одно из свойств фрактала — самоподобие. Другое свойство фрактала — дробность. Дробность фрактала является математическим отражением меры неправильности фрактала.

Ковер Серпинского

Рисунок 1 — Фрактал «ковер Серпинского»

Фактически все, что кажется случайным и неправильной может быть фракталом, например, облака, деревья, изгибы рек, биения сердца, популяции и миграции животных или языки пламени.

Данный фрактал получается путем проведения ряда итераций. Итерация (от лат. Iteratio — повторение) — повторное применение какой-либо математической операции. Рисунок 2 — Построение ковра Серпинского

Хаотический аттрактор является фракталом. Почему? У странного аттрактора, также как и в фрактале по мере увеличения выявляется все больше деталей, т.е. срабатывает принцип самоподобия.

Как бы мы не меняли размер аттрактора, он всегда останется пропорционально одинаковым. В техническом анализе типичным примером фрактала являются волны Эллиота, где также работает принцип самоподобия.

Приложения

Библиография

• (en) Майкл Барнсли , Fractals Everywhere , Морган Кауфманн  (en) ( ISBN  0-12-079061-0 )
• Андре Дофине, фрактальная география , Hermès-Lavoisier, 2011 ( ISBN  978-2-7462-3798-8 )
• (ru) Герман А. Дуарте, Фрактальный рассказ. О взаимосвязи между геометрией и технологией и ее влиянии на повествовательные пространства , Transcript Verlag  (de) , 2014 ( ISBN  978-3-8376-2829-6 )
• Жак Дюбуа и Жан Шален , Мир фракталов , 2006, Editions Ellipses ( ISBN  978-2-7298-2782-3 ) .
• (en) Кеннет Фалконер  (en) , Фрактальная геометрия , 1990, John Wiley & Sons ( ISBN  0-471-92287-0 )
• Пьер Франкаузер , Фрактальность городских структур , Economica , 1994
• (en) Бенуа Мандельброт , Фрактальная геометрия природы , 1982, WH Freeman ( ISBN  0-7167-1186-9 ) . Trad. : Фрактальные объекты. Формы, случайность и измерение , Фламмарион , 2- е  изд., 1984.
• (en) Хайнц-Отто Пейтген  (де) , Наука о фрактальных изображениях , 1988, Springer ( ISBN  0-387-96608-0 ) .
• (ru) Хайнц-Отто Пейтген, Фракталы для класса , Нью-Йорк, Спрингер, 1993
• Д. Кейрос-Конде, Ж. Шалин и Ж. Дюбуа, La Nature Trans-scale, 2015, Эллипсы
• Бернар Саповал, Универсальности и фракталы , Фламмарион, сб. Поля

• Автоподобие
• Фрактальное искусство
• Бенуа Мандельброт (биография и история его открытия)
• Конструктивная теория
• Хаусдорфово измерение
• Детерминизм
• Эффект Дросте
• Список фракталов по размерности Хаусдорфа
• Рекурсия
• Кристаллеровская модель
• Тротуар Пенроуза
• Относительность масштаба
• Фрактальная вселенная
• , научно-фантастический рассказ Мишеля Жери (1980)
• Mise en abyme
• Теория корневищ ( детерриториализация )

Внешние ссылки

• Ресурс, связанный со здоровьем

  (ru)  Медицинские тематические рубрики

   :

• Авторитетные записи  :
  • ( )

Фракталы
Характеристики	Фрактальные измерения Асвад  (ru) Минковский-Булиган Хаусдорф Рекурсия Автоподобие
Система повторяющихся функций	Барнсли Ферн Набор кантора Кох Флаке Губка менгера Серпинский ковер Серпинский треугольник Кривые Бланманже Cesàro Рам  (ru) Дракон Золотой дракон Госпер Гильберта Лебег Леви Кривая заполнения кривая Пеано заливка снежинки Коха Серпинский  (ru)
L-система	Фрактал навеса  (ru) Кривая заполнения
Создание	Горящий корабль Юлия Ляпунов Мандельброт Ньютон Tricorn  (en) Mandelbox Mandelbulb
Фотореалистичные методы рендеринга	Буддхаброт Орбитальная ловушка  (ru) Ядро Пикавера  (en)
Случайные фракталы	Броуновское движение Фрактальный ландшафт Теория перколяции Самоизбегающий путь
Личности	Георг Кантор Феликс хаусдорф Гастон Джулия Хельге фон Кох Пол Леви Александр Ляпунов Бенуа Мандельброт Льюис Фрай Ричардсон Вацлав Серпинский
Список фракталов по размерности Хаусдорфа Фрактальное искусство Теория Хаоса (книга)

Л. Карпентер: искусство, созданное природой

Теория фракталов довольно быстро нашла практическое применение. Так как она весьма тесно связана с визуализацией самоподобных образов, то первыми, кто взял на вооружение принципы и алгоритмы построения этих необычных форм, стали художники. Первым из них стал будущий основатель студии Pixar Лорен Карпентер. Работая над презентацией прототипов самолетов, ему в голову пришла идея в качестве фона использовать изображение гор. Сегодня с такой задачей сможет справиться практически каждый пользователь компьютера, а в семидесятых годах прошлого века ЭВМ были не в состоянии выполнять такие процессы, ведь графических редакторов и приложений для трехмерной графики на тот момент еще не было. И вот Лорену попалась книга Мандельброта «Фракталы: форма, случайность и размерность». В ней Бенуа приводил множество примеров, показывая, что существуют фракталы в природе (фыва), он описывал их разнообразную форму и доказывал, что они легко описываются математическими выражениями. Данную аналогию математик приводил в качестве аргумента полезности разрабатываемой им теории в ответ на шквал критики от своих коллег. Они утверждали, что фрактал — это всего лишь красивая картинка, не имеющая никакой ценности, являющаяся побочным результатом работы электронных машин. Карпентер решил опробовать этот метод на практике. Внимательно изучив книгу, будущий аниматор стал искать способ реализации фрактальной геометрии в компьютерной графике. Ему понадобилось всего три дня, чтобы визуализировать вполне реалистичное изображение горного ландшафта на своем компьютере. И сегодня этот принцип широко используется. Как оказалось, создание фракталов не занимает много времени и сил.