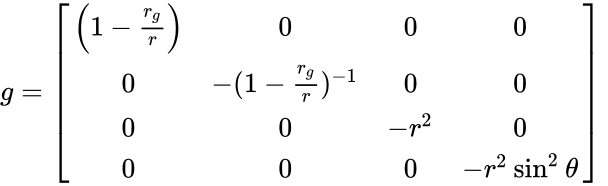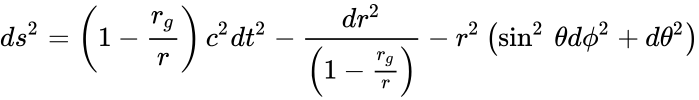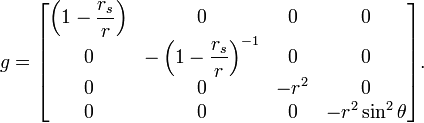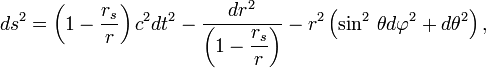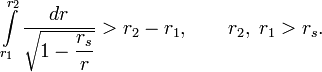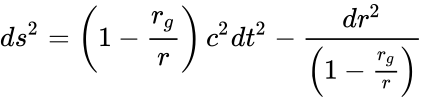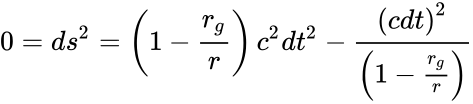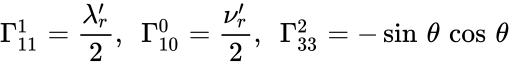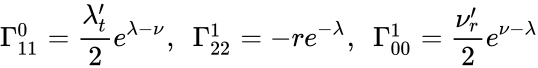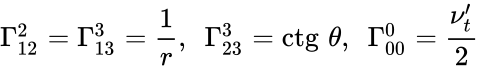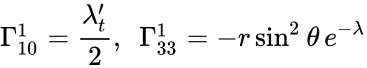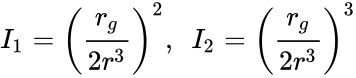Внешние ссылки [ править ]
| Викискладе есть медиафайлы по теме Карла Шварцшильда . |
- О’Коннор, Джон Дж .; Робертсон, Эдмунд Ф. , «Карл Шварцшильд» , архив истории математики MacTutor , Сент-Эндрюсский университет.
- Роберто Б. Сальгадо Световой конус: Черная дыра Шварцшильда
- Некролог в Astrophysical Journal , написанный Эйнаром Герцшпрунгом
- Карл Шварцшильд на проекте « Математическая генеалогия»
- Биография Карла Шварцшильда, написанная Индрану Сухендро, Журнал Абрахама Зельманова , 2008, Том 1.
| vтеОтносительность | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Специальная теория относительности |
|
||||||||||||
| Общая теория относительности |
|
||||||||||||
| Ученые |
|
||||||||||||
| Категории |
► Теория относительности |
| Авторитетный контроль |
|
|---|
Вид метрики
В координатах
![]()
, пространственная часть которой аналогична (но не совпадает!) сферической системе координат, метрический тензор имеет вид
Интервал в этой метрике записывается как
где
— так называемый гравитационный радиус тела. Координата r не является длиной радиус-вектора, а вводится так, чтобы длина окружности с центром в начале координат в данной метрике была равна
. При этом, расстояние до центра даётся интегралом
При
или
метрика Шварцшильда переходит в метрику Минковского в сферических координатах, так что пространство-время вдали от массивного тела оказывается плоским. Так как
при
и
монотонно возрастает с ростом
, то собственное время в точках вблизи тела течёт медленнее, чем вдалеке от него, то есть происходит своеобразное замедление времени массивными телами.
1. Вид метрики
1.1. Шварцшильдовские координаты
В так называемых Шварцшильдовских координатах , из которых 3 последних аналогичны сферическим, метрический тензор наиболее физически важной части пространства-времени Шварцшильда с топологией (произведение области двумерного евклидова пространства и двумерной сферы) имеет вид
Интервал в этой метрике записывается как
где — так называемый радиус Шварцшильда, или гравитационный радиус, M — масса, создающая гравитационное поле (в частности, масса чёрной дыры), G — гравитационная постоянная, c — скорость света.
Координата r не является длиной радиус-вектора, а вводится так, чтобы площадь сферы в данной метрике была равна . При этом «расстояние» между двумя событиями с разными r (но одинаковыми остальными координатами) даётся интегралом
При или метрика Шварцшильда стремится (покомпонентно) к метрике Минковского в сферических координатах, так что вдали от массивного тела M пространство-время оказывается приблизительно псевдоевклидовым сигнатуры (1,3). Так как при r > rs и g00 монотонно возрастает с ростом r, то собственное время в точках вблизи тела «течёт медленнее», чем вдалеке от него, то есть происходит своеобразное гравитационное замедление времени массивными телами.
1.2. Дифференциальные характеристики
Обозначим
Тогда не равные нулю независимые символы Кристоффеля имеют вид
Инварианты тензора кривизны равны
Тензор кривизны относится к типу по Петрову.
1.3. Дефект массы
Если имеется сферически симметричное распределение материи «радиуса» (с точки зрения координат) a, то полная масса тела может быть выражена через его тензор энергии-импульса по формуле
В частности, для статического распределения вещества , где — плотность энергии в пространстве. Учитывая, что объём шарового слоя в выбранных нами координатах равен
получим, что
Это различие выражает собой гравитационный дефект массы тела. Можно сказать, что часть полной энергии системы содержится в энергии гравитационного поля, хотя локализовать эту энергию в пространстве невозможно.
1.4. Особенность в метрике
На первый взгляд, метрика содержит две особенности: при r = 0 и при r = rs. Действительно, в Шварцшильдовских координатах частице, падающей на тело, потребуется бесконечно большое время для достижения поверхности r = rs, однако переход, например, к координатам Леметра в сопутствующей системе отсчёта показывает, что с точки зрения падающего наблюдателя никакой особенности пространства-времени на данной поверхности нет, причём как сама поверхность, так и область будут достигнуты за конечное собственное время.
Реальная особенность метрики Шварцшильда наблюдается лишь при , где стремятся к бесконечности скалярные инварианты тензора кривизны. Эта особенность (сингулярность) не может быть устранена сменой системы координат.
1.5. Горизонт событий
Поверхность r = rs называется горизонтом событий. При более удачном выборе координат, например в координатах Леметра или Крускала, можно показать, что никакие сигналы не могут выйти из чёрной дыры через горизонт событий. В этом смысле не удивительно, что поле вне Шварцшильдовской чёрной дыры зависит лишь от одного параметра — полной массы тела.
Фотосинтез
Многие века ученые ломали голову над проблемой питания растений. Поначалу считалось, что питание происходит через корневую систему. Но простой опыт наблюдения за деревом в течение нескольких лет показал, что его вес увеличился на несколько десятков килограммов, а вес почвы в кадке изменился лишь на несколько сот грамм. Тогда на долгое время популярной стала гипотеза о водном питании растений.
Опыт Джозефа Пристли совершил настоящий прорыв в области биологии. Ученый помещал под стеклянный колпак горящую свечу и лабораторную мышь. Через некоторое время свеча гасла, а мышь задыхалась из-за недостатка кислорода. Пристли, руководствуясь интуицией, решил посмотреть, что будет с комнатным растением в тех же условиях.
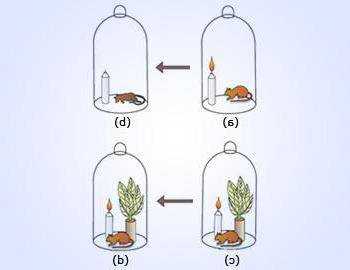
К его удивлению, растение не только не умерло, но и очистило «загрязненный» воздух под колпаком. Свеча продолжала гореть, а мышь – жить. Ученый не смог самостоятельно объяснить, почему так происходит, но благодаря его открытию наука сделала большой шаг в понимании процесса фотосинтеза.
Проверка решения Шварцшильда
Формула метрики Шварцшильда получена теоретически после долгого вывода и многих предположений.
Каждое решение задачи должно проходить проверку, для вывода о правильности результата.
Такой проверкой является решение с помощью полученной формулы интервала для луча света вдоль радиуса.
Исходным положением в Теории Относительности является определение расстояния
как произведение скорости света на время, затраченное светом на преодоление этого пространства.
Подставим в полученную формулу нулевые приращения углов
Тогда
Направим луч света вдоль радиуса. За время
луч пройдёт расстояние
- Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle dr =сdt}
кроме того для луча света интервал равен нулю :
При этих подстановках уравнение будет:
Видно, что уравнение при этих условиях выполняется при расстоянии
Решение Шварцшильда непригодно для применения в Гравитации.
____________________________
Обозначим
Тогда не равные нулю независимые компоненты символов Кристоффеля имеют вид
Инварианты тензора кривизны равны
Тензор кривизны относится к типу D по Петрову.
Работа в науке
В 20 лет Шварцшильд окончил Страсбурский университет, в 23 года — Мюнхенский университет со степенью доктора. Затем три года работал ассистентом в обсерватории Кюффнера близ Вены. В 1899 г. Шварцшильд стал приват-доцентом Мюнхенского университета, а в 1901 г. — профессором и директором обсерватории Гёттингенского университета. Шварцшильд был избран членом Академии наук в 1905 г.
С 1909 г. Шварцшильд занимал должность директора Потсдамской астрофизической обсерватории. В том же году вступил в брак с нееврейкой (родители обоих противились этому союзу). В 1913 году он стал членом Берлинской академии и профессором в университете.
История получения и интерпретации
Метрика Шварцшильда, выступая как объект значительного теоретического интереса, для специалистов-теоретиков является также неким инструментом, с виду простым, но тем не менее сразу же приводящим к трудным вопросам.
В середине 1915 года Эйнштейн опубликовал предварительные уравнения теории гравитации . Это были ещё не уравнения Эйнштейна, но они уже совпадали с окончательными в вакуумном случае . Сферически-симметричные уравнения для вакуума Шварцшильд проинтегрировал в период с 18 ноября 1915 г. до конца года. 9 января 1916 г. Эйнштейн, к которому Шварцшильд обратился по поводу публикации своей статьи в «Berliner Berichte», написал ему, что «прочитал его работу с огромной страстью» и «был ошеломлён, что истинное решение этой проблемы можно выразить столь легко» — Эйнштейн исходно сомневался, возможно ли вообще получить решение таких сложных уравнений.
Шварцшильд закончил свою работу в марте, получив также сферически-симметричное статическое внутреннее решение для жидкости с постоянной плотностью. В это время на него навалилась болезнь (пузырчатка), которая в мае свела его в могилу. С мая 1916 г. И. Дросте, ученик Г. А. Лоренца, проводя исследования в рамках окончательных эйнштейновских уравнений поля, получил решение той же задачи более простым методом, чем Шварцшильд. Ему же принадлежит первая попытка анализа расходимости решения при стремлении к сфере Шварцшильда.
Вслед за Дросте большинство исследователей стали удовлетворяться различными соображениями, направленными на доказательство непроницаемости сферы Шварцшильда. При этом соображения теоретического характера подкреплялись физическим аргументом, согласно которому «такое в природе не существует», поскольку отсутствуют тела, атомы, звёзды, радиус которых был бы меньше шварцшильдовского радиуса.
Для К. Ланцоша, а также для Д. Гилберта сфера Шварцшильда стала поводом задуматься над понятием «сингулярность», для П. Пенлеве и французской школы она являлась объектом полемики, в которую включился Эйнштейн.
В ходе парижского коллоквиума 1922 г., организованного в связи с приездом Эйнштейна, речь зашла не только об идее, согласно которой радиус Шварцшильда не будет сингулярным, но также и о гипотезе, предвосхищающей то, что сегодня называют гравитационным коллапсом.
Искусная разработка Шварцшильда имела лишь относительный успех. Ни его метод, ни его интерпретация не были взяты на вооружение. Из его работы не сохранили почти ничего, кроме «голого» результата метрики, с которой связали имя её создателя. Но вопросы интерпретации и прежде всего вопрос «сингулярности Шварцшильда» тем не менее решены не были. Cтала выкристаллизовываться точка зрения, что эта сингулярность не имеет значения. К этой точке зрения вели два пути: с одной стороны, теоретический, согласно которому «сингулярность Шварцшильда» непроницаема, и с другой стороны, эмпирический, состоящий в том, что «этого в природе не существует». Эта точка зрения распространились и стала доминирующей во всей специальной литературе того времени.
Следующий этап связан с интенсивным исследованием вопросов гравитации в начале «золотого века теории относительности».
Протестанты неправославного вероисповедания
Евангелисткие христиане и баптисты официально имеют
церковь в России с 1867 года. До этого момента они были причислены к «сектантам»
и подвергались гонениям. По этой причине найти метрические книги баптистской
церкви ранее 1867 года практически невозможно.
Однако, встретить упоминания о ваших предках, если
они имели такое неправославное вероисповедание, можно в полицейских отчетах.
А также в православных исповедных росписях по нужному населенному пункту. Всех не явившихся на исповедь и причастие перед Пасхой отмечали в исповедной росписи. Указывалась причина отсутствия, в том числе и иное вероисповедание. За такими людьми обычно пристально следила местная полиция.
Сектантские общины неправославного вероисповедания
К сектантским общинам русская православная церковь относила почти все объединения неправославного вероисповедания, за исключением указанных выше. Ими занимались полицейские, проводя дознания.
Православные священники должны были следить за вверенным участком, чтобы не появлялись никакие секты. Всех, кто не являлся на исповедь, обязательно проверяли, проводя разъяснительную и просветительскую работу.
Документы с упоминаниями религиозных сект в Российской
империи можно найти в архивах примерно по 1919 – 1922 гг.
Книги с метрическими записями церквей разных конфессий необходимо искать в региональных архивах. Если им на хранение такие не поступали, то обратитесь к справочнику по административно-территориальному делению. Возможно нужный населенный пункт относился к другой губернии.
Вам будут интересны другие статьи по генеалогии:
⠀⠀⠀⠀
Работа в науке
В 20 лет Шварцшильд окончил Страсбурский университет, в 23 года — Мюнхенский университет со степенью доктора. Затем три года работал ассистентом в обсерватории Кюффнера близ Вены. В 1899 г. Шварцшильд стал приват-доцентом Мюнхенского университета, а в 1901 г. — профессором и директором обсерватории Гёттингенского университета. Шварцшильд был избран членом Академии наук в 1905 г.
С 1909 г. Шварцшильд занимал должность директора Потсдамской астрофизической обсерватории. В том же году вступил в брак с нееврейкой (родители обоих противились этому союзу). В 1913 году он стал членом Берлинской академии и профессором в университете.
Работа в науке
В 20 лет Шварцшильд окончил Страсбурский университет, в 23 года — Мюнхенский университет со степенью доктора. Затем три года работал ассистентом в обсерватории Кюффнера близ Вены. В 1899 г. Шварцшильд стал приват-доцентом Мюнхенского университета, а в 1901 г. — профессором и директором обсерватории Гёттингенского университета. Шварцшильд был избран членом Академии наук в 1905 г.
С 1909 г. Шварцшильд занимал должность директора Потсдамской астрофизической обсерватории. В том же году вступил в брак с нееврейкой (родители обоих противились этому союзу). В 1913 году он стал членом Берлинской академии и профессором в университете.
Новый виток и первые продажи
Только через 13 лет проживающий в Швейцарии часовщик, ювелир и очередной изобретатель Иоган Якоб Швепп усовершенствовал сатуратор Бергмана.Швепп начал выпускать в промышленных масштабах газированные, но пока несладкие, напитки. К действию его подтолкнула мечта о создании безалкогольного шампанского.
Через некоторое время Швепп решил удешевить и упростить производство. Вместо настоящего углекислого газа стали использовать обычную пищевую соду. Так появилась полюбившаяся англичанам содовая. В 1792 году промышленник основал компанию Schwepp&Cо, существующую поныне и известную под названием Schweppes.

Лишь через 14 лет после смерти Якоба Швеппа впервые впустили сладкий лимонад. А вскоре в напиток начали добавлять фруктовые соки и недавно открытую и выделенную лимонную кислоту.
В 1851 году производство приобрело такой размах, что на Большой Лондонской выставке, которую компания обеспечивала напитками, был организован фонтан, заполненный газировкой от Schwepp&Cо. Кстати, этот фонтан до сих пор украшает логотип Schweppes.
Не менее случайно и сообща было изобретено мороженое на палочке, которое позже назвали эскимо.
Мне нравитсяНе нравится
Интересная история Раф кофе – кто придумал рецепт популярного напитка
В июле 2012 года на индийский город Каннур пролился кровавый дождь
В прошлом веке детей выгуливали в оконных клетках
Первый сыр начали делать более десяти тысяч лет назад
Интересные факты о минералах, происхождение, применение, свойства
На английских кладбищах некоторые могилы закрыты клетками
Полярные день и ночь, где наблюдаются, сколько длятся, как влияют на человека
Интересные факты о мороженом, возникновение, популярность, виды
Особенности дореволюционного документоведения
Как известно, грамотность не была сильной стороной Российской империи. По статистике до 1917 года были неграмотными около 80% населения. Образование часто велось в церковно-приходских школах с соответствующим уровнем обучения. Это и многое другое налагалось на ведение гражданской документации. Организация которой в провинции была довольно посредственного уровня, и велась с привлечением церкви.
На последнюю вплоть до Октябрьской революции возлагалась функция регистрации актов гражданского состояния. Обязанности государственных регистраторов выполняли священники (в других религиях — имамы, раввины и др.). Потому крещение и отпевание также считалось актом гражданского состояния. Журналами регистрации гражданских актов тогда служили церковные метрические книги, благодаря которым устанавливалась метрика (родословная) того или иного человека. Ныне эти метрические книги перекочевали в государственные архивы, где к ним могут получить доступ многие исследователи.
С 17 века в Российской империи стали регулярно проводится переписи населения. Данные таких переписей (к примеру, всеобщей переписи 1897 года) сегодня находятся в различных государственных архивах. Благодаря последним исследователи могут помочь получить информацию о своих предках до революции по их фамилии.
Могут также помочь узнать данные о своих предках ряд следующих ресурсов:
-
vgd.ru – сайт всероссийского генеалогического древа. Там вы сможете найти огромную базу данных о людях, связанных с Россией. На ресурсе имеется большой форум с огромным количеством участников, где вам помогут ценным советом;
-
gwar.mil.ru/heroes/ – ресурс памяти героев Первой мировой войны (1914-1918 годов), на котором вы можете отыскать нужного вам человека бесплатно и без регистрации;
- myheritage.com – популярный интернациональный ресурс, который поможет в воссоздании генеалогического древа вашей семьи;
- familyspace.ru – популярный генеалогический ресурс с функцией социальной сети;
-
books.google.ru – в этой огромной библиотеке Гугл доступны тысячи оцифрованных изданий. Просто вбейте в поисковую строку имя и фамилию искомого вами человека, и вполне вероятно, что вы найдёте упоминания о своих предках;
-
jewishgen.org/new – ресурс по еврейской генеалогии.
Алгоритм пользования такими ресурсами довольно прост. Вы переходите на нужный ресурс, и в поисковой строке вводите фамилию нужного человека и жмёте на кнопку поиска. Через несколько мгновений вы получите данные по найденным совпадениям, сможете скачать найденные релевантные документы о ваших предках до революции и так далее.
Жизнь [ править ]
Карл Шварцшильд родился 9 октября 1873 года во Франкфурте-на-Майне в семье евреев . Его отец был активен в деловом сообществе города, и у семьи были предки в городе, восходящие к шестнадцатому веку. Один из его братьев — художник Альфред Шварцшильд . Карл посещал еврейскую начальную школу до 11 лет. Он был чем-то вроде вундеркинда, опубликовав две статьи по бинарным орбитам ( небесной механике ) до того, как ему исполнилось шестнадцать. Он учился в Страсбурге и Мюнхене , получив докторскую степень в 1896 году за работу об Анри Пуанкаре.Теории.
С 1897 года работал ассистентом в Венской обсерватории Каффнера .
С 1901 по 1909 год он был профессором престижного института в Геттингене , где у него была возможность поработать с некоторыми значительными фигурами, включая Давида Гильберта и Германа Минковского . Шварцшильд стал директором обсерватории в Геттингене . В 1909 году он женился на Эльзе Позенбах, дочери профессора хирургии из Геттингена. Позже в том же году они переехали в Потсдам , где он занял пост директора Астрофизической обсерватории. Тогда это была самая престижная должность, доступная для астронома в Германии. У него и Эльзы было трое детей, Агата (которая была профессором классической литературы в Университете Отаго.в Данидине, Новая Зеландия), Мартин (впоследствии ставший профессором астрономии в Принстонском университете) и Альфред.
Могила Карла Шварцшильда в Штадтфридхоф (Геттинген)
С 1912 года Шварцшильд был членом Прусской академии наук .
С началом Первой мировой войны в 1914 году он присоединился к немецкой армии, несмотря на то, что ему было больше 40 лет. Он служил как на западном, так и на восточном фронтах, дослужившись до звания лейтенанта артиллерии.
Во время службы на фронте в России в 1915 году он начал страдать от редкого и болезненного аутоиммунного кожного заболевания, называемого пузырчаткой . Тем не менее ему удалось написать три выдающиеся работы: две по теории относительности и одну по квантовой теории . Его работы по теории относительности привели к первым точным решениям уравнений поля Эйнштейна , и небольшая модификация этих результатов дает хорошо известное решение, которое теперь носит его имя — метрику Шварцшильда .
Борьба Шварцшильда с пузырчаткой, возможно, в конечном итоге привела к его смерти 11 мая 1916 года.
Координаты Крускала
Можно попытаться ввести координаты, не дающие сингулярности при . Таких координатных систем известно множество, и самой часто встречающейся из них является система координат Крускала, которая покрывает одной картой всё максимально продолженное многообразие, удовлетворяющее вакуумным уравнениям Эйнштейна (без космологической постоянной). Это большее пространство-время называется обычно (максимально продолженным) пространством Шварцшильда или (реже) пространством Крускала. Метрика в координатах Крускала имеет вид
где , а функция определяется (неявно) уравнением .
Рис. 1. Сечение пространства Шварцшильда. Каждой точке на рисунке соответствует сфера площадью . Светоподобные геодезические (то есть мировые линии фотонов) — это прямые под углом к вертикали, иначе говоря — это прямые или
Пространство максимально, то есть его уже нельзя изометрически вложить в большее пространство-время, а область в координатах Шварцшильда () является всего лишь частью (это область — область I на рисунке). Тело, движущееся медленнее света — мировая линия такого тела будет кривой с углом наклона к вертикали меньше , см. кривую на рисунке — может покинуть . При этом оно попадает в область II, где . Покинуть эту область и вернуться к оно, как видно из рисунка, уже не сможет (для этого пришлось бы отклониться более, чем на от вертикали, то есть превысить скорость света). Область II таким образом представляет собой чёрную дыру. Её граница (ломаная, ) соответственно является горизонтом событий.
В есть ещё одна асимптотически плоская область III, в которой также можно ввести Шварцшильдовы координаты. Однако эта область причинно не связана с областью I, что не позволяет получить о ней никакой информации, оставаясь снаружи от горизонта событий. В случае реального коллапса астрономического объекта области IV и III просто не возникают, так как левую часть представленной диаграммы необходимо заменить на непустое пространство-время, заполненное коллапсирующей материей.
Отметим несколько замечательных свойств максимально продолженного Шварцшильдовского пространства :
- Оно сингулярно: координата наблюдателя, падающего под горизонт, уменьшается и стремится к нулю, когда его собственное время стремится к некоторому конечному значению . Однако его мировую линию нельзя продолжить в область , так как точек с в этом пространстве нет. Таким образом, судьба наблюдателя нам известна только до некоторого момента его (собственного) времени.
- Хотя пространство статично (видно, что метрика (1) не зависит от времени), пространство таковым не является. Это формулируется более строго так: вектор Киллинга, являющийся из времениподобным в , в областях II и III расширенного пространства становится пространственноподобным.
- Область III тоже изометрична . Таким образом, максимально продолженное пространство Шварцшильда содержит две «вселенные» — «нашу» (это ) и ещё одну такую же. Область II внутри чёрной дыры, соединяющая их, называется мостом Эйнштейна — Розена. Попасть во вторую вселенную наблюдатель, стартовавший из I и движущийся медленнее света, не сможет (см. рис. 1), однако в промежуток времени между пересечением горизонта и попаданием на сингулярность он сможет увидеть её. Такая структура пространства-времени, которая сохраняется и даже усложняется при рассмотрении более сложных чёрных дыр, породила многочисленные рассуждения на тему возможных «других» вселенных и путешествий в них через чёрные дыры как в научной литературе, так и в научно-фантастической (см. Кротовые норы).