Основы механики для «чайников» (часть 3): релятивистская механика

Постулаты СТО

СТО полностью выводится на физическом уровне строгости из пяти постулатов
(предположений):

1. Справедлив принцип
   относительности Пуанкаре-Эйнштейна, являющийся расширением принципа относительности
   Галилея на все явления.
2. Скорость света не зависит
   от скорости движения как источников, так и
   приёмников во всех инерциальных системах отсчёта. Это позволяет
   дистанционно произвести однозначную первоначальную синхронизацию всех
   имеющихся часов как в неподвижной, так и в
   движущейся системе отсчёта.
3. Справедливость симметрий
   относительно поворотов в пространстве-времени Евклида.
4. Справедливость симметрий
   относительно сдвигов в пространстве-времени Евклида.
5. Пространственно-временные
   измерения осуществляются с помощью электромагнитных волн.

Формулировка второго постулата может быть шире: «Скорость света постоянна во
всех инерциальных системах отсчёта», но для вывода СТО достаточно его
формулировки, записанной выше. Некоторые постулаты сформулированы явно, а
другие предполагаются неявным образом как в работах
Эйнштейна, так и Пуанкаре, хотя и в разной степени.

Иногда пятый постулат СТО записывают как синхронизацию часов по А.
Эйнштейну, но принципиального значения это не имеет: при различных условиях
синхронизации изменяется математическое описание экспериментальной ситуации без
изменения предсказываемых и измеряемых эффектов. Пятый постулат СТО является
ключевым, так как без него скорость света не смогла бы появиться в
преобразованиях Лоренца для координат и времени и в других формулах.

Раньше можно было встретить утверждение о том, что СТО обосновывает
существование скорости света как предельной скорости распространения сигналов.
Естественно, что это не может быть доказано в рамках СТО, которая
не является теорией о распространении сигналов, а лишь использует свет в
процессе измерений.

Кинетическая энергия

Кинетическая энергия при скоростях, приближающихся к скорости света, вычисляется как разность между кинетической энергией движущегося тела и кинетической энергией тела, находящегося в состоянии покоя:

где m

– масса объекта;

v

– скорость движения объекта;

c

— скорость света в вакууме;

mc 2

– энергия покоя.

Данную формулу можно привести к такому виду:

При скоростях, значительно меньших скорости света, это выражение переходит в формулу кинетической энергии классической механики:

T = 1/2mv 2

Скорость света является предельным значением. Быстрее света не может двигаться ни одно тело.

Многие задачи смогло бы решить человечество, если бы удалось создать аппараты, способные передвигаться со скоростью, близкой к скорости света. Пока люди об этом только мечтают. Но когда-нибудь полёт с релятивистской скоростью станет реальностью.

Релятивистская механика – это механика, в которую превращается механика Ньютона в случае если тело движется со скоростью, близкой к скорости света. На таких высоких скоростях с вещами начинают происходить ну просто волшебные и совершенно неожиданные вещи, такие как, например, релятивистское сокращение длины или замедление времени.

Но как именно классическая механика становится релятивистской? Обо всем по порядку в нашей новой статье.

Начнем с самого начала…

Преобразования Галилея

Преобразования Галилея в классической механике – это преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Не будем приводить здесь всех вычислений и выводов, а просто запишем формулу для преобразования скорости. Согласно этой формуле скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела в движущейся системе отсчета и скорости движущейся системы отсчета относительно неподвижной.

Приведенный нами выше принцип относительности Галилея является частным случаем принципа относительности Эйнштейна.

Принцип относительности Эйнштейна и постулаты СТО

В начале двадцатого века после более чем двухсотлетнего господства классической механики возник вопрос о распространении принципа относительности на немеханические явления. Причиной возникновения такого вопроса стало закономерное развитие физики, в частности оптики и электродинамики. Результаты многочисленных экспериментов то подтверждали справедливость формулировки принципа относительности Галилея для всех физических явлений, то в ряде случаев указывали на ошибочность преобразований Галилея.

Эйнштейн — человек, создавший специальную теорию относительности

Например, проверка формулы сложения скоростей показала ее ошибочность при скоростях, близких к скорости света. Более того, опыт Физо в 1881 году показал, что скорость света не зависит от скорости движения источника и наблюдателя, т.е. в любой системе отсчета остается постоянной. Данный результат эксперимента никак не укладывался в рамки классической механики.

Решение этой и других проблем нашел Альберт Эйнштейн. Для того чтобы теория сошлась с практикой, Эйнштейну пришлось отказаться от нескольких, казалось бы, очевидных истин классической механики. А именно — предположить, что расстояния и промежутки времени в различных системах отсчета не неизменны. Ниже приведем основные постулаты Специальной Теории Относительности (СТО) Эйнштейна:

Первый постулат: во всех инерциальных системах отсчета все физические явления протекают одинаково.  При переходе от одной системы к другой все законы природы и явления, описывающие их,  инвариантны, то есть никакими опытами нельзя отдать предпочтение одной из систем, ибо они инвариантны.

Второй постулат: скорость света в вакууме одинакова во всех направлениях и не зависит от источника и наблюдателя, т.е. не изменяется при переходе от одной инерциальной системы к другой.

Преобразования координат и времени при переходе от неподвижной системы отсчета к системе, движущейся со скоростью света, называются преобразованиями Лоренца. К примеру, пусть одна система покоится, а вторая движется вдоль оси абсцисс.

Здесь

Как видим, время также изменяется наряду с координатами, то есть выступает как бы в роли четвертной координаты. Преобразования Лоренца показывают, что в СТО пространство и время неразделимы в отличие от классической механики.

Помните парадокс двух близнецов, один из которых ждал на земле, а второй летел на космическом корабле с очень большой скоростью? После того как брат-космонавт вернулся на землю, он застал своего брата стариком, хотя сам был практически так же молод, как в момент начала путешествия. Типичный пример того, как изменяется время в зависимости от системы отсчета.

Парадокс близнецов

При скоростях же много меньших скорости света преобразования Лоренца переходят в преобразования Галилея. Даже при скорости современных реактивных самолетов и ракет отклонения от законов классической механики настолько малы, что их практически невозможно измерить.

Полная энергия

Полная энергия ​\( E \)​ тела в состоянии движения называется релятивистской энергией тела:

Полная энергия, масса и импульс тела связаны друг с другом – они не могут меняться независимо.

Закон пропорциональности массы и энергии – один из самых важных выводов СТО. Масса и энергия являются различными свойствами материи. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами.

Важно!
Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах – в этом заключается содержание закона сохранения энергии. Пропорциональность массы и энергии является выражением внутренней сущности материи

Сокращение расстояний

Если движущийся наблюдатель посылает световой сигнал в сторону своего движения, то, согласно постулатам СТО, скорость света для всех наблюдателей одинакова. А это значит, что расстояния, которые измеряет движущийся наблюдатель с точки зрения покоящегося, уменьшились. И для нахождения скоростей и координат требуется использовать формулы релятивистской механики – преобразования Лоренца. В соответствии с этими преобразованиями, если между точками покоящегося тела расстояние равно $l_0$, то при движении этого тела со скоростью $v$ (вдоль направления измерения), для покоящегося наблюдателя расстояние между точками будет равно:

$$l=l_0\sqrt{1-{v^2\over c^2}}$$

Отметим, что оба значения верны и равноправны. Расстояние, измеренное покоящимся наблюдателем, ничуть не «более правильное», чем измеренное движущимся, хотя $l_0 \geq l$.

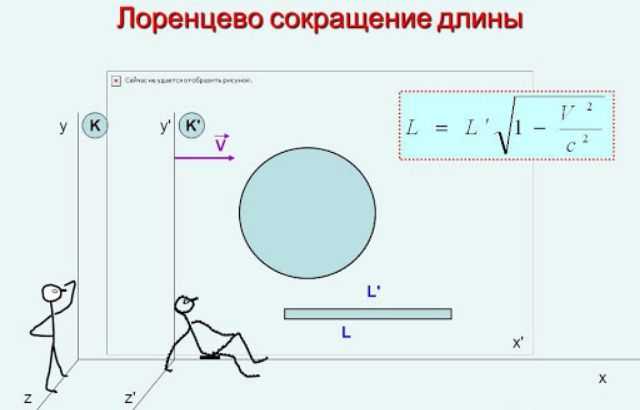Рис. 2. Лоренцево сокращение длины.

Комментарии

Так же, как и в случае квантовой механики, многие предсказания теории
относительности противоречат интуиции, кажутся невероятными и невозможными.
Это, однако, не означает, что теория относительности неверна. В
действительности то, как мы видим (либо хотим видеть) окружающий нас мир и то,
каким он является на самом деле, может сильно различаться. Уже больше века
учёные всего мира пробуют опровергнуть СТО. Ни одна из этих попыток не смогла
найти ни малейшего изъяна в теории. О том, что теория верна математически,
свидетельствует строгая математическая форма и чёткость всех формулировок.

О том, что СТО действительно описывает наш мир,
свидетельствует огромный экспериментальный опыт. Многие следствия этой теории
используются на практике. Очевидно, что все попытки «опровергнуть
СТО» обречены на провал потому, что сама теория опирается на три постулата
Галилея (которые несколько расширены), на основе которых построена ньютонова механика, а также на дополнительные постулаты.
Результаты СТО не вызывают какого-либо сомнения в пределах максимальной
точности современных измерений: лучше 10 − 12,
а в некоторых аспектах — до 10 − 15.
Более того, точность их проверки является настолько высокой, что постоянство
скорости света положено в основание определения метра — единицы длины, в
результате чего скорость света становится константой автоматически, если
измерения вести в соответствии с метрологическими требованиями и при
обязательном использовании стандартной процедуры измерений на основе
электромагнитных волн.

Литература

• Г. А. Лоренц. Интерференционный опыт
  Майкельсона. Из книги «Versucheiner Theoriederelektrischenundoptischen Erscheinungeninbewegten
  Korpern. Leiden, 1895,
  параграфы 89…92.
• J. Larmor. On a Dynamical Theory of the
  Electric and Luminiferous Medium, Part 3,
  Relations with material media.— 1897, Т. 190. — С. 205-300.
• А. Пуанкаре. Измерение
  времени. «Revuede Metaphysiqueetde
  Morale», 1898, t.
  6, p. 1…13.
• Lorentz H.A. Zittingsverlag,
  Acad.Wet., v.7, s.507 (1899); Amsterdam Proc.,
  1898-1899, p.427).
• Larmor J.J. Aether
  and Matter. Cambridge, 1900, (p.167-177).
  /На русском яз. см. с.48. Принцип относительности — М.: Атомиздат, 1973, (сост. сб. А.Тяпкин).
• А. Пуанкаре.
  Оптические явления в движущихся телах. ElectriciteetOptique, G. CarreetC.
  Naud, Paris, 1901, p. 535…536.
• А. Пуанкаре. О
  принципе относительности пространства и движения. Главы 5…7 из книги
  “Наука и гипотеза”(H. Poinrare. Scienceand Hypothesis. Paris, 1902.)
• А. Пуанкаре.
  Настоящее и будущее математической физики. Доклад, напечатанныйвжурнале
  «Bulletindes Sciences Mathematiques»,
  1904, v. 28, ser. 2, p. 302.
• Г. А. Лоренц.Электромагнитные
  явления в системе движущейся с любой скоростью, меньшей скорости света. Proc Acad., Amsterdam, 1904, v 6,
  p. 809.
• А. Эйнштейн. К
  электродинамике движущихся тел. Ann. d. Phys.,1905 (рукопись поступила 30 июня 1905 г.),
  b. 17, s. 89.
• А. Пуанкаре. О
  динамике электрона. Rendicontidel Circolo Matematicodi
  Palermo, 1906 (рукописьпоступила 23 июля 1905 г.) v. XXI, p. 129.

Дополнительная
литература

• Паули В. Теория
  относительности. Изд. 2-е, испр. и доп. Перев. с
  нем. — М.: Наука, 1983. — 336 с.
• Эйнштейн А. Сущность
  теории относительности. — М.: Изд. ин. лит., 1955. — 157 с.
• Кузьмичев В.Е. Законы и
  формулы физики/ Отв. ред. В.К. Тартаковский.-Киев:
  Наук.думка, 1989. С.84-88. ISBN 5120004938. Кузьмичев
  В.Е. Законы и Формулы физики.
• Селезнев Ю.А. Основы
  элементарной физики. Учебное пособие. Издательство «Наука»,
  Главная редакция физико-математической литературы, М., 1974г., С.78-79. Сайт для высылки
  книги в электронном виде.
• Физическая энциклопедия,
  т.2 — М.: Большая Российская Энциклопедия. Физическая энциклопедия.

Специальная теория относительности

Специальная теория относительности (СТО) — теория локальной структуры пространства-времени . Впервые была представлена в 1905 году Альбертом Эйнштейном в работе «К электродинамике движущихся тел». Теория описывает движение, законы механики , а также пространственно-временные отношения, определяющие их, при любых скоростях движения, в том числе и близких к скорости света . Классическая механика Ньютона в рамках специальной теории относительности является приближением для малых скоростей. СТО может применяться там, где можно ввести инерциальные системы отсчёта (хотя бы локально); она неприменима для случаев сильных гравитационных полей, существенно неинерциальных систем отсчёта и при описании глобальной геометрии Вселенной (кроме частного случая плоской пустой стационарной Вселенной).

Специальная теория относительности возникла как разрешение противоречия между классической электродинамикой (включая оптику) и классическим галилеевским принципом относительности . Последний утверждает, что все процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Это означает, в частности, что любые механические
эксперименты в закрытой системе не позволят определить без наблюдения внешних по отношению к ней тел, как она движется, если её движение равномерно и прямолинейно. Однако оптические
эксперименты (например, измерение скорости распространения света в разных направлениях) внутри системы в принципе должны были бы обнаружить такое движение. Эйнштейн распространил принцип относительности и на электродинамические явления, что, во-первых, дало возможность описать практически весь круг физических явлений с единых позиций, а во-вторых, позволило объяснить результаты эксперимента Майкельсона — Морли (в котором не было обнаружено никакого влияния квазиинерциального движения Земли на скорость распространения света). Принцип относительности стал первым постулатом новой теории. Однако непротиворечивое описание физических явлений в рамках расширенного принципа относительности стало возможным лишь ценой отказа от ньютоновского абсолютного евклидового пространства и абсолютного времени и их объединения в новый геометрический конструкт — псевдоевклидово пространство-время , в котором расстояния и временные промежутки между событиями трансформируются определённым образом (посредством преобразований Лоренца) в зависимости от системы отсчёта, из которой они наблюдаются. Это потребовало введения дополнительного принципа — постулата инвариантности скорости света . Таким образом, специальная теория относительности базируется на двух постулатах:

1. Все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Формально в пределе бесконечной скорости света формулы специальной теории относительности переходят в формулы классической механики.

Эффекты СТО

К наиболее распространенным эффектам СТО, их ещё называют релятивистскими
эффектами, относят:

Замедление
времени

Время в движущейся системе отсчета течет медленнее:

,

где — промежуток времени между двумя событиями в
движущейся со скоростью системе отсчёта, —
промежуток времени между этими же событиями, отсчитываемый в покоящейся системе
отсчёта.

С этим эффектом связан так называемый парадокс близнецов.

Сокращение
линейных размеров

Линейные размеры тел в движущейся системе отсчета сокращаются:

, для длины.

, для объема.

Такое сокращение размеров еще называют лоренцевым
сокращением.

«Утяжеление» при
движении

Релятивистская масса движущегося объекта больше массы покоя:

.

Однако, в современной физической литературе по СТО — масса
частицы (инвариантная масса) не зависит от скорости, являясь инвариантом
относительно преобразований Лоренца, и является величиной неаддитивной. В
данной формуле речь идет о так называемой «релятивистской массе», которая возрастает
с увеличением скорости. «Утяжеление» следует понимать лишь условно, как будто
справедлив закон Ньютона, а не аналогичный ему закон релятивистской динамики. В
современной физической литературе понятие «релятивисткой массы» практически
заменено на понятие «массы-энергии», и встречается в основном в ранних работах
по теории относительности.

Следует подчеркнуть обратимость эффектов СТО. Например, эффект замедления
времени в движущейся системе отсчёта 2 относительно неподвижной системы 1
отсчёта справедлив и для наблюдателя в движущейся системе – для него его
собственная система отсчёта 2 неподвижна, и с его точки зрения замедляться
время будет в системе отсчёта 1, движущейся в противоположную сторону. Это же
касается и видимого сокращения размеров движущихся тел. Данные эффекты являются
следствием принятой в СТО процедуры измерения времени и размеров посредством
электромагнитной волны и процедуры установления одновременности, то есть связи
между пространственной координатой тех или иных часов и временем регистрации
события этими часами.

Создание СТО

Предпосылкой к созданию теории относительности явилось развитие в XIX веке
электродинамики. Результатом обобщения и теоретического осмысления
экспериментальных фактов и закономерностей в областях электричества и
магнетизма стали уравнения Максвелла, описывающие все проявления
электромагнитного поля и его взаимодействие с зарядами и токами.

Другим следствием развития электродинамики стал переход от
ньютоновской концепции дальнодействия, согласно которой взаимодействующие на
расстоянии тела воздействуют друг на друга через разделяющую их пустоту, причём
взаимодействие осуществляется с бесконечной скоростью, т.е. «мгновенно», к
концепции близкодействия, предложенной Майклом Фарадеем, в которой
взаимодействие передаётся с помощью промежуточных агентов – полей, заполняющих
пространство – и при этом встал вопрос о скоростях распространения как
взаимодействий, переносимых полями, так и самих полей. Скорость
распространения электромагнитного поля в пустоте вытекала из уравнений
Максвелла и оказалась постоянной и равной скорости света.

В связи с этим появляется новый вопрос — относительно чего постоянна
скорость света? В максвелловой электродинамике
скорость распространения электромагнитных волн (при условии измерения этой
скорости с помощью электромагнитных часов и положения часов с помощью света)
оказалась не зависящей от скоростей движения как
источника этих волн, так и наблюдателя. Аналогичной оказалась
и ситуация с магнитостатическими решениями, вытекающими из уравнений Максвелла:
статические магнитные поля и силы Лоренца, действующие на движущиеся в
магнитных полях заряды, зависят от скоростей зарядов по отношению к
наблюдателю, т.е. уравнения Максвелла оказались неинвариантными относительно
принципа относительности и преобразований Галилея – что противоречило
ньютоновской концепции абсолютного пространства классической механики.

Специальная теория относительности была разработана в конце
XIX – начале XX века
усилиями Г. А. Лоренца, А. Пуанкаре, Д. Лармора и А.
Эйнштейна, и затем представлена Г. Минковским в
четырёхмерном формализме, объединяющем пространство и время. Вопрос
приоритета в создании СТО имеет дискуссионный характер: основные положения и
полный математический аппарат теории, включая групповые свойства преобразований
Лоренца, в абстрактной форме были впервые сформулированы А. Пуанкаре в работе
1905 г. «О динамике электрона» на основе предшествующих результатов Г. А.
Лоренца, а явный абстрактный вывод базиса теории — преобразований Лоренца, из
минимума исходных постулатов был дан А. Эйнштейном в практически
одновременной работе 1905 г. «К электродинамике движущихся сред». Однако Лармор ещё в 1897 г., до работы Лоренца 1899 г.,приходит к преобразованиям Лоренца. Он такжедаёт релятивистскую формулу сложения
скоростей (смотри LarmorJ.J., 1900).

Опыт Майкельсона

Основная статья: Опыт
Майкельсона

Основой для создания СТО и предшествующих теорий послужил опыт Майкельсона,
который дал результат измерения, неожиданный для классической физики своего
времени. Попытка проинтерпретировать этот результат в начале XX века вылилась в
пересмотр классических представлений механики, и создание Лоренцом,
Пуанкаре и Эйнштейном релятивистских физических теорий.

Релятивистские эффекты

Из преобразований Лоренца вытекают релятивистский эффект замедления времени и лоренцово сокращение длины.

Замедление времени

Этот удивительный эффект заключается в том, что при скоростях, сравнимых со скоростями света, время течёт с разной скоростью. И чем выше скорость объекта, тем медленнее течёт в нём время.

Количественное значение замедления времени получают из преобразований Лоренца:

где ∆t

— время, проходящее между двумя событиями движущегося объекта, за которым следит неподвижный наблюдатель,

∆t o

— время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя, находящегося в движении,

v

— относительная скорость движения объекта,

c

— скорость света в вакууме.

Из формулы видно, что ∆ to

˃ ∆ t

. То есть, для наблюдателя, находящегося в движении, время движется медленнее, чем для того, который находятся в состоянии покоя.

Очень наглядно эффект замедления времени проявляется в космических полётах, где движение происходит с релятивистскими скоростями. Ведь время на борту космического корабля течёт медленнее, чем на Земле. Так, если аппарат будет двигаться со скоростью, равной 0,95 скорости света, его полёт будет длиться 12 земных лет, но по часам на самом корабле пройдёт всего 7,3 года. А если корабль будет находиться в полёте 64 года по своему времени, то на Земле за это время пробежит уже 5 млн. лет. И кто знает, возможно, не только ход часов, но и ход всех процессов в полёте будет замедленным. И в будущем, возвратившись на Землю из длительного полёта, космонавты могут обнаружить, что их дети оказались старше их.

Лоренцово сокращение длины

Это сокращение называют также релятивистским сокращением длины движущегося тела или масштаба.

Длина любого объекта в релятивистской механике зависит от скорости. Этот эффект проявляется в том, что для наблюдателя предметы, движущиеся относительно него, имеют меньшую длину, чем в реальности. И чем больше скорость движения предмета, тем меньшим он кажется. При скорости, приближающейся к скорости света, длина предмета вдоль направления движения приближается к нулю. Именно поэтому наблюдатель, следящий за шаром, движущимся с такой скоростью, вместо него увидит плоский диск.

Следует уточнить, что эффект сокращения длины наблюдается только при скоростях, близких к скорости света.

Скорость распространения света

Когда мы включаем свет, комната озаряется светом моментально. Поэтому кажется, что свету нисколько не нужно времени, чтобы достигнуть стен. Но это не так, просто свет распространяется с такой большой скоростью, что это непросто заметить в обычных условиях.

Впервые конечность скорости света удалось установить О. Рёмеру (датскому ученому) в 1676 г. Он наблюдал за затмением Ио — спутника Юпитера. Он видел, как ИО проходил перед планетой, а затем погружался в ее тень и пропадал из поля зрения. Затем он опять появлялся, как мгновенно вспыхнувшая лампа. Промежуток времени между двумя вспышками был равен 42 ч 28 мин. Поэтому спутник представлял для астронома космические часы, которые посылали сигналы на Землю через равные промежутки времени.

Сначала Рёмер делал измерения, когда Земля при своем движении вокруг Солнца подошла к Юпитеру максимально близко. Затем он повторил их в момент, когда Земля максимально удалилась от Юпитера. Измерения показали, что во втором случае спутник появился на 22 минуты позже по сравнению с первым результатом. Ученый объяснил это явление так: «Если бы я мог остаться на другой стороне земной орбиты, то спутник всякий раз появлялся бы из тени в назначенное время; наблюдатель, находящийся там, увидел бы Ио на 22 минуты раньше. Запаздывание в этом случае происходит оттого, что свет употребляет 22 мин на прохождение от места моего первого наблюдения до моего теперешнего положения».

Зная опаздывание появления Ио и расстояние, которым оно вызвано, можно определить скорость, разделив это расстояние на время опаздывания. Из-за неточности измерений и неточного знания радиуса земной орбиты Рёмер получил скорость света, равную 215 000 км/с. Если провести расчеты с более точными данными, результат получается максимально приближенным к реальному значению скорости света — около 300 000 км/с.

Позже измерения скорости света повторили другие ученые. В 1849 году И. Физо (французский ученый) сделал расчеты, в результате которых он получил значение 313 000 км/с. В 1856 году была измерена скорость света в воде, которая оказалась в 4/3 раз меньше по сравнению со скоростью света в космосе (вакууме). Так же было установлено, что скорость света в средах всегда меньше скорости света в вакууме.

По современным данным принято считать, что скорость света равна 299 792 458 м/с с точностью ±1,2 м/с. Обозначают эту величину как c. Единица измерения в СИ — м/с.

Внимание!

При выполнении расчетных задач скорость света принято принимать за величину c = 3∙108 м/с.

Сущность СТО

Следствием постулатов СТО являются преобразования Лоренца, заменяющие собой
преобразования Галилея для нерелятивистского, «классического» движения. Эти
преобразования связывают между собой координаты и времена одних и тех же
событий, наблюдаемых из различных инерциальных систем отсчёта.

В СТО видоизменяются также и законы динамики. Так, можно вывести, что второй
закон Ньютона, связывающий силу и ускорение, должен быть модифицирован при
скоростях тел, близких к скорости света. Кроме того, можно показать, что и
выражение для импульса и кинетической энергии тела имеет более сложную
зависимость от скорости, чем в нерелятивистском случае.

Специальная теория относительности получила многочисленные подтверждения на
опыте и является безусловно верной теорией в своей
области применимости. Учёт достижений экспериментальной физики позволяет
утверждать, что в пределах своей области применимости – при пренебрежении
эффектами гравитационного
взаимодействия тел – СТО является справедливой с очень высокой степенью
точности (до 10−12 и выше) (см. список
литературы). По меткому замечанию Л. Пэйджа «В наш
век электричества, вращающийся якорь каждого генератора и каждого электромотора
неустанно провозглашает справедливость теории относительности — нужно лишь
уметь слушать».

Четырёхмерный
континуум — пространство-время

С математической точки зрения, непривычные свойства СТО можно
интерпретировать как результат того, что время и пространство не являются
независимыми понятиями, а образуют единый четырёхмерный континуум —
пространство-время Минковского, которое является псевдоевклидовым
пространством. Вращения базиса в этом четырёхмерном
пространстве-времени, смешивающие временную и пространственные координаты
4-векторов, выглядят для нас как переход в движущуюся систему отсчета и похожи
на вращения в обычном трёхмерном пространстве. При этом естественно
изменяются проекции четырёхмерных интервалов между определёнными событиями на временную и пространственные оси системы отсчёта, что и
порождает релятивистские эффекты изменения временных и пространственных
интервалов. Именно инвариантная структура этого пространства, задаваемая
постулатами СТО, не меняется при переходах от одного события к другому, и
гарантирует независимость результатов экспериментов от используемой
инерциальной системы отсчёта.

Аналог расстояния между событиями в пространстве Минковского, называемый
интервалом, при введении наиболее простых координат, аналогичных декартовым
координатам трёхмерного пространства, даётся выражением:

Обратите внимание: теоретически «квадрат расстояния» между двумя разными
событиями может быть не только положительным, но и отрицательным и даже нулём.
Именно незнакоопределённость метрики определяет
свойства пространства-времени, делая его геометрию псевдоевклидовой (см. напр

световой конус).

Релятивистская кинематика

Релятивистская четырехскорость, то есть четырехвектор, представляющий скорость в теории относительности, определяется следующим образом:

Uзнак равноdИксdτзнак равно(cdтdτ,dИксdτ){\ displaystyle {\ boldsymbol {\ mathbf {U}}} = {\ frac {d {\ boldsymbol {\ mathbf {X}}}} {d \ tau}} = \ left ({\ frac {cdt} {d \ tau}}, {\ frac {d \ mathbf {x}} {d \ tau}} \ right)}

В приведенном выше примере — собственное время пути в пространстве-времени , называемое мировой линией, за которым следует скорость объекта, представленная выше, и
τ{\ displaystyle {\ tau}}

Иксзнак равно(cт,Икс){\ Displaystyle {\ boldsymbol {\ mathbf {X}}} = (ct, \ mathbf {x})}

это четыре-положения ; координаты события . Из-за замедления времени правильное время — это время между двумя событиями в системе отсчета, где они происходят в одном и том же месте. Собственное время связано с координатным временем t соотношением:

dτdтзнак равно1γ(v){\ displaystyle {\ frac {d \ tau} {dt}} = {\ frac {1} {\ gamma (\ mathbf {v})}}}

где — фактор Лоренца :
γ(v){\ Displaystyle {\ gamma} (\ mathbf {v})}

γ(v)знак равно11-v⋅vc2⇌γ(v)знак равно11-(vc)2.{\ displaystyle \ gamma (\ mathbf {v}) = {\ frac {1} {\ sqrt {1- \ mathbf {v} \ cdot \ mathbf {v} / c ^ {2}}}} \, \ rightleftharpoons \, \ gamma (v) = {\ frac {1} {\ sqrt {1- (v / c) ^ {2}}}}.}.

(можно цитировать любую версию), поэтому следует:

Uзнак равноγ(v)(c,v){\ Displaystyle {\ boldsymbol {\ mathbf {U}}} = \ гамма (\ mathbf {v}) (с, \ mathbf {v})}

Первые три члена, за исключением фактора , представляют собой скорость, видимую наблюдателем в его собственной системе отсчета. Определяются скоростью между опорным кадром наблюдателя и кадром объекта, который является кадром , в котором измеряется его надлежащее время. Эта величина инвариантна относительно преобразования Лоренца, поэтому, чтобы проверить, что видит наблюдатель в другой системе отсчета, нужно просто умножить четырехвектор скорости на матрицу преобразования Лоренца между двумя системами отсчета.
γ(v){\ Displaystyle {\ гамма (\ mathbf {v})}}γ(v){\ Displaystyle {\ гамма (\ mathbf {v})}}v{\ displaystyle \ mathbf {v}}