Механические волны ⋆ спадило

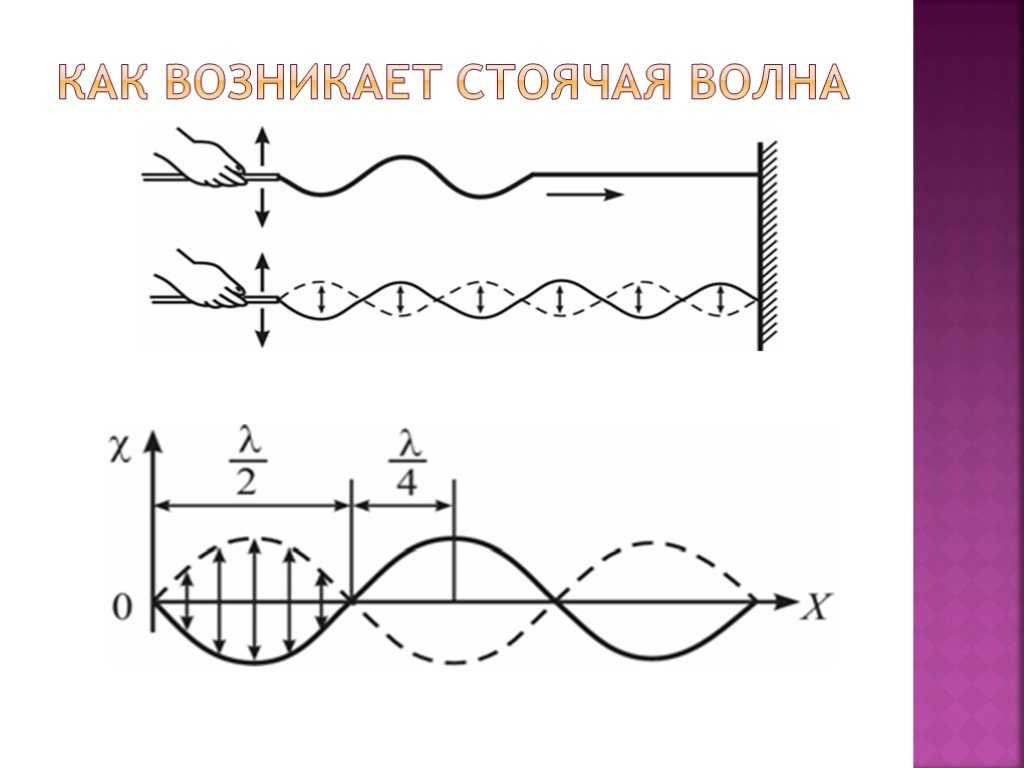
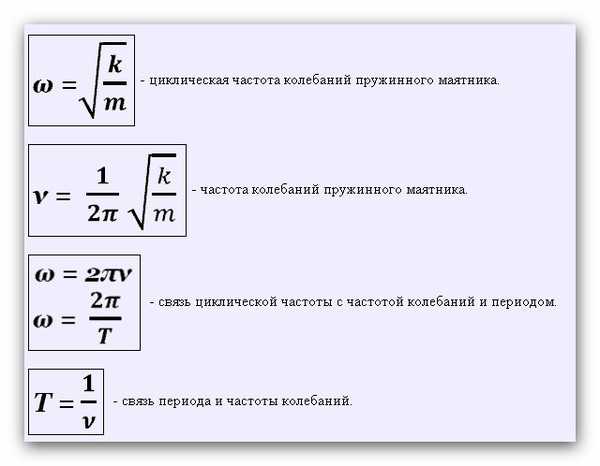
Параметры гармонического колебания

Любой колебательный процесс — это изменения некоторого параметра около среднего значения. Колебания бывают периодическими (маятник) и непериодическими (флаг на ветру). Если построить график колебательного процесса, то среднее значение на нём будет представлено горизонтальной прямой, а значение колеблющегося параметра — кривой, постоянно возвращающейся к среднему. При этом для непериодического колебания возвраты будут хаотичными, а для периодического — строго через одинаковый промежуток времени. Этот промежуток называется периодом колебания $T$.

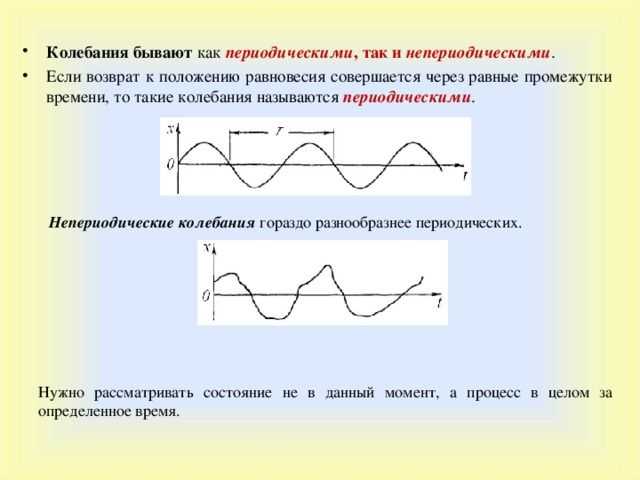
Рис. 1. Периодические и непериодические колебания.

Простейшим периодическим колебанием является колебание, которое совершается по закону круговых функций (синуса или косинуса). Оно называется гармоническим. Поскольку в высшей математике доказывается, что любое колебание (в том числе непериодическое) можно представить в виду бесконечной суммы гармонических колебаний, то в первую очередь изучаются именно они. А по определению любое гармоническое колебание можно представить в виде функции:

$$A=A_0sin \Bigg ( {2\pi\over T} t +\varphi_0 \Bigg ),$$

где:

$A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
$T$ — период колебаний;
$t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
$\varphi_0$ — начальная фаза колебаний.

Коэффициент ${2\pi\over T}=\omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2\pi\over T} t +\varphi_0=\varphi$, которое является аргументом функции синуса, называется полной фазой колебания.

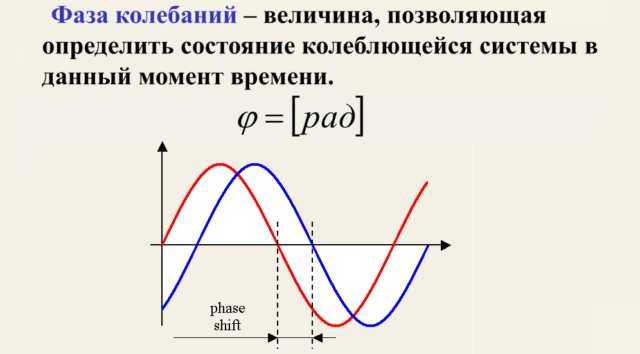
Рис. 2. Фаза колебания.

Разность фаз

Для одного колебательного процесса фаза не играет большой роли. В самом деле, если брать разные моменты времени за начальные, мы можем получать любое значение фазы, колебательный процесс при этом никак не изменится. Однако, когда речь идет о нескольких колебательных процессах, то значение фазы существенно возрастает. Именно фазой определяется разница мгновенных значений двух колебаний.

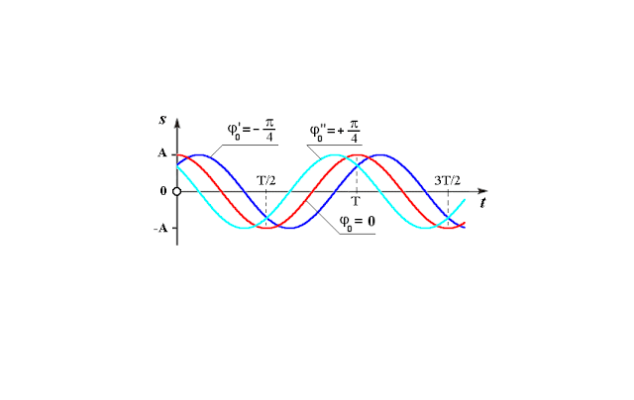Рис. 3. Графики колебаний с различными фазами.

Если частоты колебаний неодинаковы, то каждый момент времени фазы будут различны, их разность также будет изменяться. Если же частоты колебаний одинаковы, то несмотря на изменение со временем фазы каждого колебания, разность фаз этих двух колебаний будет постоянной. Это может приводить к интересным ситуациям.

Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза будет равна нулю, а у второго — $\pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Более того, если эти колебания сложить, то их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противофазе.

Что мы узнали?

Фаза колебания — это часть периода колебания, соответствующая текущему моменту времени. Единица измерения фазы — радиана, она имеет период $2\pi$

Особо важное значение имеет разность фаз двух и более колебаний. Если частота этих колебаний одинакова, то и разность фаз будет всегда постоянной

/10

Вопрос 1 из 10

Действие [ править | править код ]

Одна из наиболее фундаментальных физических величин, на которой построено современное описание практически любой достаточно фундаментальной физической системы — действие — по своему смыслу является фазой.

Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс. Для гармонических колебаний:

где φ = ωt + φ — фаза колебания, А — амплитуда, ω — круговая частота, t — время, φ — начальная (фиксированная) фаза колебания; в момент времени t = 0φ = φ. Фаза выражается в радианах.

Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции (см. рис. ниже), которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения

равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Максимальная кинетическая энергия груза маятника

Частота колебаний маятника

Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.

Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

где $ x $ – координата тела – смещение тела от положения равновесия в данный момент времени; $ A $ – амплитуда колебаний; $ \omega t+\varphi_0 $ – фаза колебаний; $ \omega $ – циклическая частота; $ \varphi_0 $ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

где $ v $ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

где $ a $ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где $ F $ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где $ W_k $ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:

потенциальная энергия равна нулю;
кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

кинетическая энергия равна нулю;
потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

наличие источника звука;
наличие упругой среды между источником и приемником звука;
наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

инфразвук ($ \nu $ < 16 Гц);
звуковой диапазон (16 Гц < $ \nu $ < 20 000 Гц);
ультразвук ($ \nu $ > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Начальная фаза. Сдвиг фаз

В начальный момент времени t = 0 фаза

φ = ωt + φ (1.6.1)

имеет значение φ. Это значение фазы называется начальной фазой.

Два или несколько гармонических колебаний с одинаковыми частотами и амплитудами могут отличаться друг от друга только начальными фазами. Между колебаниями имеется разность фаз, или, как часто говорят, сдвиг фаз φ_с. Если начальная фаза первого колебания равна φ₀₁, а второго φ₀₂, то сдвиг фаз второго колебания относительно первого равен:

φ_c = φ₀₂ — φ₀₁. (1.6.2)

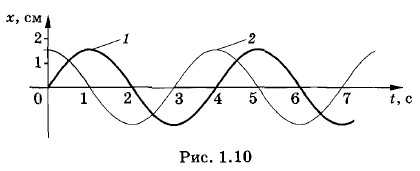
На рисунке 1.10 изображены графики колебаний, сдвинутых по фазе на . График 1 соответствует колебаниям, совершающимся по синусоидальному закону с начальной фазой, равной нулю (φ₀₁ = 0):

x₁ = х_m sin ωt

График 2 соответствует колебаниям, сдвинутым по фазе на :

Начальная фаза этих колебаний

Так как то

x₂ = x_m cos ωt.

Таким образом, колебания, описываемые синусом и косинусом, представляют собой колебания со сдвигом фаз .

Параметры гармонического колебания

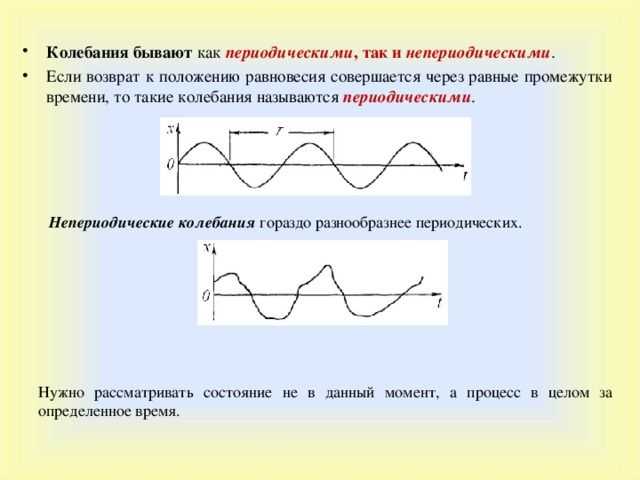
Рис. 1. Периодические и непериодические колебания.

$$A=A_0sin Bigg ( {2piover T} t +varphi_0 Bigg ),$$

где:

$A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
$T$ — период колебаний;
$t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
$varphi_0$ — начальная фаза колебаний.

Коэффициент ${2piover T}=omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2piover T} t +varphi_0=varphi$, которое является аргументом функции синуса, называется полной фазой колебания.

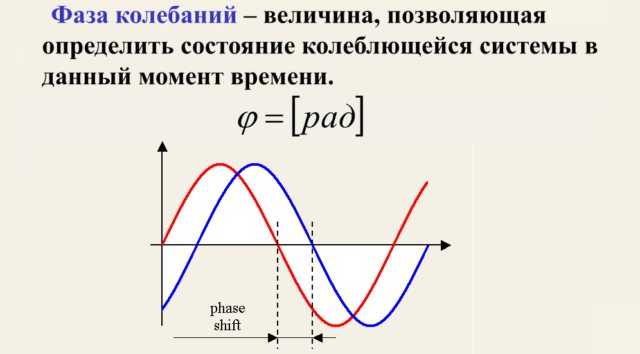
Рис. 2. Фаза колебания.

Заземление: безопасность зелено-желтого цвета

Заземление или защитный проводник – это, прежде всего, безопасность. А безопасность в электрике дорогого стоит.

Этот кабель выполняет функцию запасного игрока. И вступает в игру лишь в том случае, когда нарушена изоляция фазного или нулевого проводника. Проще говоря, без заземления неисправный электроприбор в момент соприкасания ударит человека, с заземлением – нет.

Именно поэтому сейчас различная бытовая техника, другие приборы выпускается с защитным кабелем. Заземление в обязательном порядке должна иметь электропроводка дома.

Провода заземления обеспечивают безопасность работы электричества в доме

Заземление обозначают сочетанием pe – сокращенно от словосочетания Protective Earthing. Иногда пишут слово «земля». На схемах графически означенный кабель может быть обозначен специальными символами:

Если разбирать цветовое обозначение, то, согласно ГОСТу Р50462, для данного вида кабеля используются желто-зеленые цвета. В жестком одножильном проводе основным является зеленый цвет, отороченный желтой полоской. В мягком многожильном в качестве основного цвета применяется желтый. Продольная полоска, напротив, зеленая. Бывают нестандартные варианты цветовой маркировки защитных соединений. В этом случае полоски имеют поперечный вид. Помимо этого, применяется только зеленая расцветка.

Зачастую заземляющий кабель идет в паре с нейтральным. Тогда к желто-зеленой раскраске прибавляется синяя каемка на концах кабеля. В этом случае меняется буквенная аббревиатура – pen.

Видео: как разобраться в цветовой маркировке прводов

Так или иначе, но ответ на вопрос, какого цвета заземление в трехжильном проводе, однозначен. Всегда нужно искать зелено-желтое сочетание.

В распределительном щитке заземление найти не сложно. Для его подключения используется специальная шина. В иных случаях, кабель крепится к корпусу и металлической двери щитка.

Разность фаз

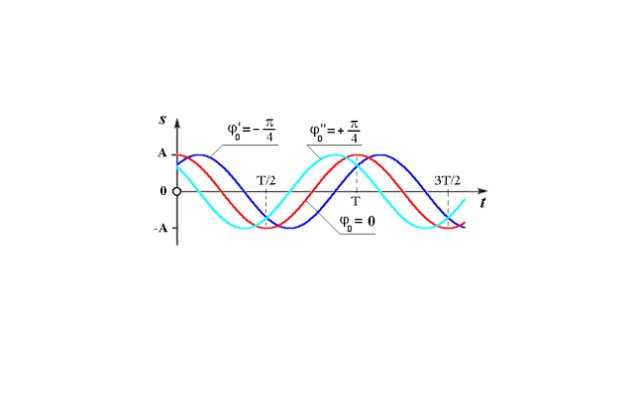
Рис. 3. Графики колебаний с различными фазами.

Физика

Фаза колебаний

При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом синуса или косинуса, равным φ = ωt + φ .

Величину φ, стоящую под знаком синуса или косинуса, называют фазой* колебаний, описываемых этими функциями. Выражается фаза в угловых единицах — радианах или градусах.

Фаза определяет не только координаты, но и другие физические величины, например скорости и ускорения, изменяющиеся по гармоническому закону.

Начальная фаза. Сдвиг фаз

В начальный момент времени t = 0 фаза

имеет значение φ. Это значение фазы называется начальной фазой.

Два или несколько гармонических колебаний с одинаковыми частотами и амплитудами могут отличаться друг от друга только начальными фазами. Между колебаниями имеется разность фаз, или, как часто говорят, сдвиг фаз φ_с. Если начальная фаза первого колебания равна φ₀₁, а второго φ₀₂. то сдвиг фаз второго колебания относительно первого равен:

φ_с = φ₀₁ + φ₀₂ (1.6.2)

На рисунке 1.10 изображены графики колебаний, сдвинутых по фазе на .

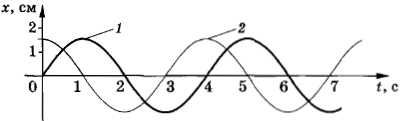
Рис. 1.10

График 1 соответствует колебаниям, совершающимся по синусоидальному закону с начальной фазой, равной нулю (φ₀₁ = 0):

График 2 соответствует колебаниям, сдвинутым по фазе на :

Начальная фаза этих колебаний φ₀₂ = .

Так как

то

Таким образом, колебания, описываемые синусом и косинусом, представляют собой колебания со сдвигом фаз .

Определение амплитуды и начальной фазы из начальных условий

Уже упоминалось, что амплитуда и начальная фаза не определяются уравнением движения. Их значения зависят от начальной координаты х(0) = x и начальной скорости х'(0) = v.

Значения x и v определяются условиями возбуждения колебаний. Если вывести тело из положения равновесия и отпустить, не сообщая ему скорости, то х(0) = x, а х'(0) = 0. Напротив, если сообщить телу начальную скорость, толкнув его в положении равновесия, то х(0) = 0, а x'(0) = v.

Рассмотрим общий случай, когда при t = 0 х(0) ≠ 0 и х'(0) ≠ 0. Выбор решения в форме синуса или косинуса повлияет на начальную фазу, но не на амплитуду. Пусть решение уравнения (1.4.1) имеет вид:

Тогда

При t = 0

Согласно уравнениям (1.6.5)

Отсюда

Это выражение определяет начальную фазу φ. В частном случае, если x = 0, то tg φ = 0 и φ = 0. Если же v = 0, то tg φ = ∞ и φ = .

Возведя в квадрат оба уравнения (1.6.6) и сложив их левые и правые части, получим:

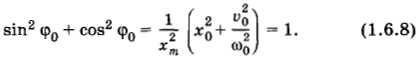
Отсюда амплитуда колебаний

При V = 0 x_m = x, а при x = 0 x_m = .

Если бы мы выразили решение не через синус, а через косинус, то амплитуда по-прежнему имела бы значение, определяемое формулой (1.6.9), а начальная фаза определялась бы уравнением

Получите это выражение самостоятельно и рассмотрите предельные случаи x = 0 и v = 0.

* От греческого слова phasis — появление, ступень развития какого-либо явления.

Характеристики колебаний

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

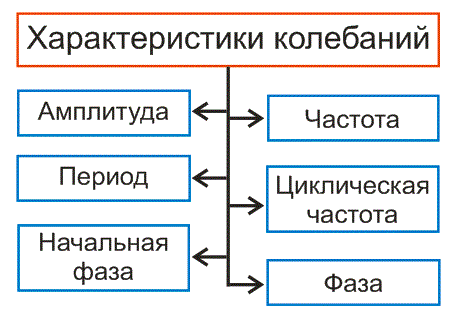
Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени $\large \Delta t$, на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Способы уменьшения гармонических составляющих

На основании полученных данных можно принимать решения о внедрении средств, направленных на уменьшение гармонических составляющих.

К основным способам уменьшения гармоник относятся разделение линейных и нелинейных нагрузок, обеспечение симметричного режима работы трехфазной системы, снижение полного сопротивления распределительной сети за счет увеличения сечения кабелей, применение линейных дросселей, применение изолирующих трансформаторов с обмотками «треугольник» и «звезда», применение пассивных и активных фильтров.

Одним из наиболее простых способов снижения уровня высших гармоник является установка линейных дросселей переменного тока. В частности, такой способ фильтрации широко применяется для подавления помех, возникающих при работе частотных преобразователей.

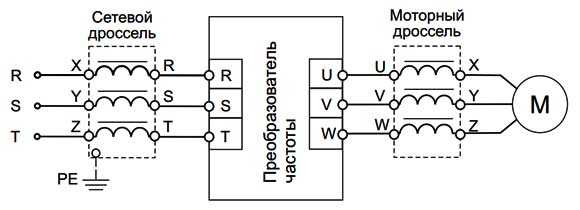
Дроссель имеет малое значение индуктивного сопротивления на основной частоте 50 Гц и большое значение сопротивления для высших гармоник, что приводит к их ослаблению. Помимо дросселей переменного тока, для частотных преобразователей могут применяться и дроссели звена постоянного тока.

Помимо дросселей широко применяются пассивные и активные фильтры.

Циклическая частота

В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.

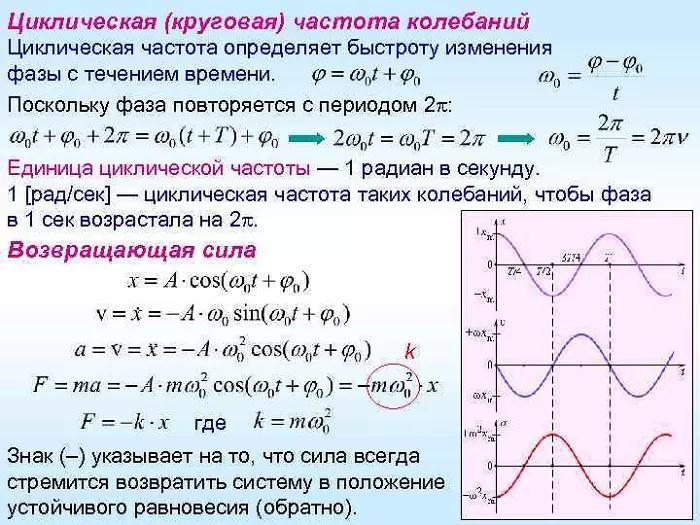
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:

ω = 2π/T = 2πν.

Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.

Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:

WLC = 1/LC.

Тогда как обычная циклическая резонансная частота выражается:

VLC = 1/2π*√ LC.

В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.